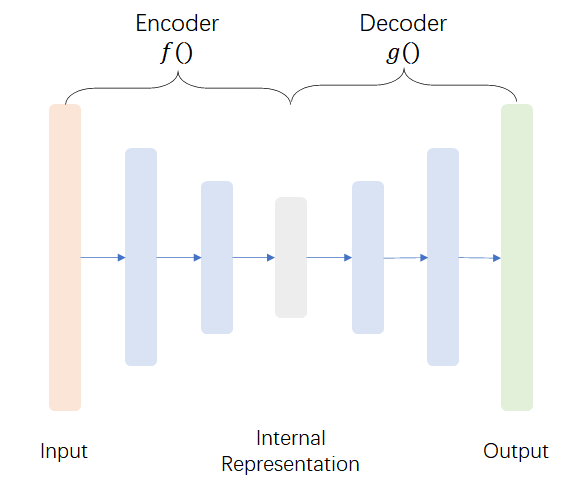
简介
生成式对抗网络(Generative Adversarial Network,GAN)基于博弈论场景,共包含两部分:判别器和生成器,其中生成器网络需要与一个判别器网络进行竞争。生成器网络\(g\)直接产生样本\(\boldsymbol{x}=g(\boldsymbol{z};\boldsymbol{\theta^{(g)}})\)(\(\boldsymbol{\theta^{(g)}}\)指生成器网络的参数),其中\(\boldsymbol{z}\)为一个向量,通常是按照均匀分布或者正态分布生成的随机噪声;而它的对手判别器网络\(d\)则试图区分从训练数据抽取的样本和从生成器抽取的样本,判别器计算得到由\(d(\boldsymbol{x};\boldsymbol{\theta}^{(d)})\)(\(\boldsymbol{\theta}^{(d)}\)为判别器网络的参数)给出的概率值,指示\(\boldsymbol{x}\)是真实训练样本而不是从模型抽取的伪造样本的概率。
![img]()
GAN网络的目标函数如下: \[
\arg \min_{g}\max_{d} V(\boldsymbol{\theta}^{(g)},\boldsymbol{\theta}^{(d)})
\] 其中\(V(\boldsymbol{\theta}^{(g)},\boldsymbol{\theta}^{(d)})\)的表达式为: \[
V(\boldsymbol{\theta}^{(g)},\boldsymbol{\theta}^{(d)})=E_{\boldsymbol{x}\sim P_{data}}[\log d(\boldsymbol{x})]+E_{\boldsymbol{x}\sim P_{G}}[\log (1-d({\boldsymbol{x}}))]
\]