引言
本文的主要内容是关于等变图神经网络的一些研究进展,简单介绍了几种用来实现等变的方法,以及在分子性质预测任务中的一些代表性网络结构的简介。注意本文的内容具有一定的时效性,主要介绍的是本文更新日期之前的工作。
基础概念
群与群表示
如果一个非空集合\(G\)上定义了一个二元运算\(\cdot\),满足如下性质:
- 封闭性,即对于\(\forall a,b\in G\),有\(a\cdot b\in G\)
- 结合律,即对于\(\forall a,b,c\in G\) ,有\((a\cdot b)\cdot c=a\cdot(b\cdot c)\)
- 存在\(e\in G\) ,使得\(\forall a\in G\),有\(a\cdot e=e\cdot a=a\) ;
- 对于\(\forall a\in G\),存在\(b\in G\),使得\(a\cdot b=b\cdot a=a\)
则称\(G\)关于运算\(\cdot\)构成一个群(group),记为\((G,\cdot)\) ,或简记为\(G\) 。在第3条性质中,\(e\)被称为单位元;在第4条性质中,\(b\)被称为\(a\)的逆元。例如全体整数对于整数加法构成一个群。
在等变图神经网络中,常见的几个群包括:
- \(O(n)\):\(n\)维正交群,包含旋转与反演操作
- \(SO(n)\):\(n\)维特殊正交群,只包含旋转操作
- \(E(n)\):\(n\)维欧几里得群,包含旋转、反演、平移操作
- \(SE(n)\):\(n\)维特殊欧几里得群,包含旋转、平移操作
设有群\(G\)和线性空间\(V\),\(V\)上的所有可逆线性变换构成一个群\(GL(V)\)。则可逆映射\(\rho(g):G\rightarrow GL(V)\)称为群\(G\)在线性空间\(V\)上的一个表示,它将群中的元素\(g\in G\)映射到线性空间\(V\)中的一个元素。一般来说,对于数域\(k\)上的\(n\)维线性空间\(V\),选定一组基后,\(V\)上的可逆线性变换\(GL(V)\)就等价于\(V\)上的可逆矩阵\(GL(n,k)\)。
例如群\(O(n)\)中的元素\(g\)可以表示为一个正交矩阵\(\rho(g)=\boldsymbol{O}_g\in R^n\);\(SO(n)\)群中的元素可以表示为一个满足\(\det(\boldsymbol{O}_g)=1\)的正交矩阵。
一个群的表示可以作用在一个\(n\)维向量\(\boldsymbol{x}\in \mathbb{R}^n\)上,即\(\rho(g)\boldsymbol{x}\),表示对这个向量做变换。例如在\(SO(n)\)群中有\(\rho(g)\boldsymbol{x}=\boldsymbol{O}_g\boldsymbol{x}\),代表对向量做旋转操作。
等变
对于群\(G\)中的任意变换,如果有 \[ \phi(\rho_{\mathcal{X}}(g)x)=\rho_{\mathcal{Y}}(g)\phi(x),\forall g\in G \] 成立,则称函数\(\phi\)在群空间\(G\)上具有等变性。其中\(\rho_{\mathcal{X}}\)和\(\rho_{\mathcal{Y}}\)分别代表输入和输出空间的群表示。例如在\(O(3)\)群中,假设输入和输出空间使用同一套坐标系,则等变关系意味着\(\phi(\boldsymbol{O}x)=\boldsymbol{O}\phi(x)\)成立;又例如对于一个平移向量\(\boldsymbol{t}\in\mathbb{R}^n\),同一坐标系下的平移等变性可以表示为\(\phi(x-\boldsymbol{t})=\phi(x)-\boldsymbol{t}\)。
特殊地,如果\(\rho_{\mathcal{Y}}(g)\)为单位元,则可以得到不变性的定义: \[ \phi(\rho_{\mathcal{X}}(g)x)=\phi(x),\forall g\in G \] 不变性可以看成是一种特殊的等变性。
等变性的实现
常用的在GNN中实现等变的方法包括:
- 不可约表示:一个紧群的线性表示可以被写为一系列不可约表示的直和,利用这一性质可以实现等变。
- 正则表达:将图卷积滤波器定义为群的函数
- 标量法:将几何向量转化为具有不变性的标量,然后将其施加在原始的向量上,从而获得等变表示。
对于以上的这些方法,下面简单介绍三个它们的代表性工作。
\(SE(3)\)-transformer
概述
SE(3)-transformer这一工作使用了\(SO(3)\)群的不可约表示来构造\(SE(3)\)等变的网络结构,它的计算过程如下:
- 在一个截断半径内寻找一个结点的邻居,以此构造图中的边
- 为每一条边\(SO(3)\)等变的权重矩阵(最重要也是最难的一步)
- 计算每条边的query,key和value
- 为每条边计算attention value,并做聚合与更新操作
上述计算过程可以总结为下图:

背景知识
球谐函数
球谐函数是一组定义在球面上的基函数,它可以从拉普拉斯方程的解中得到。考虑如下的三维拉普拉斯方程: \[ \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}+\frac{\partial^2 f}{\partial z^2}=0 \] 由于Hessian矩阵的迹具有旋转不变性(旋转之后做特征分解,再通过矩阵迹的性质可以证明迹不变),因此这个PDE的解在旋转之后仍然成立。也就是说,三维拉普拉斯方程在\(SO(3)\)群的所有元素下具有不变性。
根据这一特性,考虑在球面坐标系下对方程进行求解。方程在球面坐标系下的形式为: \[ \frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial f}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial f}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2} f}{\partial \varphi^{2}}=0 \] 使用分离变量法,将\(f\)写为\(f(r,\theta,\varphi)=R(r)Y(\theta,\varphi)\)的形式,代入上式并做分离变量操作之后可得: \[ \frac{1}{R} \frac{d}{d r}\left(r^{2} \frac{d R}{d r}\right)=\ell(\ell+1)\\ \quad \frac{1}{Y} \frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial Y}{\partial \theta}\right)+\frac{1}{Y} \frac{1}{\sin ^{2} \theta} \frac{\partial^{2} Y}{\partial \varphi^{2}}=-\ell(\ell+1) \] 再用\(Y(\theta,\varphi)=\Theta(\theta)\Phi(\varphi)\)做一次分离变量,可得: \[ -\frac{1}{\Phi} \frac{d^{2} \Phi}{d \varphi^{2}}=\ell(\ell+1) \sin ^{2} \theta+\frac{\sin \theta}{\Theta} \frac{d}{d \theta}\left(\sin \theta \frac{d \Theta}{d \theta}\right)=\lambda \] 通过求解上述方程,可得最终解的形式为: \[ f(r,\theta,\varphi)=\sum\limits_{\ell=0}^\infty\sum\limits_{m=-\ell}^\ell f_\ell^m r^\ell Y_\ell^m(\theta,\varphi) \] 其中,\(Y_\ell^m(\theta,\varphi)\)这一项代表球谐函数。
球谐函数在球坐标下的解析表达式如下: \[ Y_\ell^{m}(\theta,\varphi)= \begin{cases}\sqrt{2}K_\ell^{m}\cos(m\varphi)P_\ell^{m}(\cos\theta),& m>0\\ \sqrt{2} K_\ell^{m}\sin(-m\varphi)P_\ell^{-m}(\cos\theta),&m<0\\ K_l^0P_l^0(\cos \theta),&m=0 \\ \end{cases} \\ \] 其中,\(P_\ell^m(x)\)便是勒让德方程,\(K_\ell^m\)为系数,它们的表达式如下: \[ \begin{aligned} &P_\ell^{m}(x)=(-1)^{m}(1-x^{2})^{m/2}\dfrac{d^{m}}{dx^{m}}(P_\ell(x)), ~ P_\ell(x)=\dfrac{1}{2^{\ell}\cdot \ell!}\dfrac{d^{\ell}}{dx^{\ell}}[(x^{2}-1)^{\ell}]\\ &K_\ell^m=\sqrt{\frac{2\ell+1}{4\pi}\frac{(\ell-|m|)!}{(\ell+|m|)!}} \end{aligned} \] 将球谐函数中的\(\theta\)和\(\varphi\)转化为\(x,y,z\)并作图,即可得到它在笛卡尔坐标下的图像,如下图所示:

此外,也可以在单位球面上对其进行可视化,如下图所示:
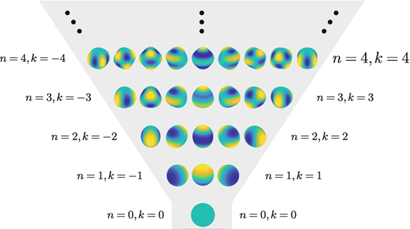
上面两图中不同的颜色代表在此位置上球谐函数的值是正数还是负数。
根据勒让德方程的正交性,球谐函数组成了球面空间\(S^2\)上的一组正交基,任意一个定义在\(S^2\)上的函数都可以表示为球谐函数的线性组合: \[ f(\boldsymbol{x})=\sum_{J\ge 0} \boldsymbol{f}_J^T\boldsymbol{Y}_J(\boldsymbol{x}),~\boldsymbol{x}\in S^2 \] 其中,\(\boldsymbol{f}_J\)代表长度为\(2J+1\)的系数向量。
下面是一个使用球谐函数对定义在球面上的函数进行重建的示例,可以看出当球谐函数的阶数取的越大则近似效果越好:

群的不可约表示
一个群\(G\)的群表示\(\rho(g):G\rightarrow GL(V)\)可以有多种不同的方式。在这些群表示中,设\(\rho\)和\(\rho'\)是两个维度相同的表示,如果它们可以用如下的相似变换来联系起来 \[ \rho'(g)=\boldsymbol{Q}^{-1}\rho(g)\boldsymbol{Q},~ \forall g\in G \] 则称两个群表示等价。
在此基础上,如果一个群表示可约,那么它可以被表示为如下的形式: \[ \rho(g)=\mathbf{Q}^{-1}\left(\rho_{1}(g) \oplus \rho_{2}(g)\right) \mathbf{Q} =\mathbf{Q}^{-1}\left[\begin{array}{ll} \rho_{1}(g) & \\ & \rho_{2}(g) \end{array}\right] \mathbf{Q},~\forall g\in G \] 在这一表达式中,如果\(\rho_1\)和\(\rho_2\)不可约,则它们被称为群\(G\)的不可约表示。也就是说,这些不可约表示相当于是一组基元,使用它们可以构造出所有其它的群表示。
实质上,所有紧群的线性表示都可以写成不可约表示的直和形式: \[ \rho(g)=\mathbf{Q}^{\top}\left[\bigoplus_{J} \mathbf{D}_{J}(g)\right] \mathbf{Q} \] 其中,\(\boldsymbol{Q}\)是一个正交的\(N\times N\)维矩阵,代表基变换矩阵。
SO(3)群的不可约表示
\(SO(3)\)群可以被表示为一个\(3\times 3\)的旋转矩阵\(\boldsymbol{R}_g\),除此之外也可以用上述不可约表示的形式来构造出其它的群表示。对于\(SO(3)\)群而言,群中的元素\(g\)被映射为大小为\((2J+1)\times (2J+1),J=0,1,2,\dots\)的矩阵\(\boldsymbol{D}_J(g)\),被称为Wigner-D矩阵,这些矩阵构成了\(SO(3)\)群的不可约表示。
根据群论中的舒尔正交关系,球谐函数可以用于构造\(SO(3)\)群的不可约表示,此时每个Wigner-D矩阵对应的正交子空间为球谐函数所对应的空间。
相应地,使用\(\boldsymbol{D}_J\)做变换的向量(\(2J+1\)维)也被称为\(\textit{type}-J\)向量,例如,Type-0向量在旋转过程中保持不变,type-1向量则根据三维旋转矩阵做旋转。
球谐函数有一个重要的特性是球谐函数的旋转操作可以直接使用Wigner-D矩阵来实现: \[ \mathbf{Y}_{J}\left(\mathbf{R}_{g}^{-1} \mathbf{x}\right)=\mathbf{D}_{J}^{*}(g) \mathbf{Y}_{J}(\mathbf{x}), \quad \mathbf{x} \in S^{2}, g \in G \]
其中,\(\boldsymbol{D}_J\)代表第J阶的Wigner-D矩阵,\(\boldsymbol{D}_J^*\)是\(\boldsymbol{D}_J\)的共轭。
基于球谐函数的旋转性质,上述函数\(f(\boldsymbol{x})\)的旋转操作也可以写为: \[ f\left(\mathbf{R}_{g}^{-1} \mathbf{x}\right)=\sum_{J \geq 0} \mathbf{f}_{J}^{\top} \mathbf{D}_{J}^{*}(g) \mathbf{Y}_{J}(\mathbf{x}), \quad \mathbf{x} \in S^{2}, g \in G \]
如果要对两个\(k\)阶和\(\ell\)阶的Wigner-D矩阵做张量乘法,则它们的张量积可以使用Clebsch-Gordan分解来计算: \[ \mathbf{D}_k(g)\otimes\mathbf{D}_\ell(g)=\mathbf{Q}^{\ell k\top}\left[\bigoplus\limits_{J=|k- \ell|}^{k+\ell}\mathbf{D}_J(g)\right]\mathbf{Q}^{\ell k} \] 其中,基变换矩阵\(\mathbf{Q}^{\ell k}\)被称为Clebsch-Gordan系数,可以直接查表得到。
备注:用一个例子说明张量积的计算规则 \[ \left.\begin{matrix}A=\left[\begin{matrix}a&b\\ c&d\end{matrix}\right]\\ B=\left[\begin{matrix}e&f\\ g&h\end{matrix}\right]\end{matrix}\right\}\Rightarrow A\otimes B=\left[\begin{matrix}aB&bB\\ cB&dB\end{matrix}\right]=\left[\begin{matrix}ae&af&be&bf\\ag&ah&bg&bh\\ ce&cf&de&df\\ cg&ch&dg&dh\end{matrix}\right] \]
\(SO(3)\)等变权重矩阵
\(SE(3)\)-transformer这一工作的重点在于构造\(SO(3)\)等变的权重矩阵。仍使用Tensor field networks这一工作中所定义的\(\mathbb{R}^3\rightarrow \mathbb{R}^{(2\ell+1)\times (2k+1)}\)的卷积操作,其中卷积核为矩阵\(W^{\ell k}\): \[ \begin{aligned} \mathbf{f}_{\mathrm{out,i}}^{\ell} & =\left[\mathbf{W}^{\ell k} * \mathbf{f}_{\mathrm{in}}^{k}\right](\mathbf{x}) \\ & =\int_{\mathbb{R}^{3}} \mathbf{W}^{\ell k}\left(\mathbf{x}^{\prime}-\mathbf{x}_{i}\right) \mathbf{f}_{\mathrm{in}}^{k}\left(\mathbf{x}^{\prime}\right) \mathrm{d} \mathbf{x}^{\prime} \\ & =\int_{\mathbb{R}^{3}} \mathbf{W}^{\ell k}\left(\mathbf{x}^{\prime}-\mathbf{x}_{i}\right) \sum_{j=1}^{N} \mathbf{f}_{\mathrm{in}, j}^{k} \delta\left(\mathbf{x}^{\prime}-\mathbf{x}_{j}\right) \mathrm{d} \mathbf{x}^{\prime} \\ & =\sum_{j=1}^{N} \int_{\mathbb{R}^{3}} \mathbf{W}^{\ell k}\left(\mathbf{x}^{\prime}-\mathbf{x}_{i}\right) \mathbf{f}_{\mathrm{in}, j}^{k} \delta\left(\mathbf{x}^{\prime}-\mathbf{x}_{j}\right) \mathrm{d} \mathbf{x}^{\prime} \\ & =\sum_{j=1}^{N} \int_{\mathbb{R}^{3}} \mathbf{W}^{\ell k}\left(\mathbf{x}^{\prime \prime}+\mathbf{x}_{j}-\mathbf{x}_{i}\right) \mathbf{f}_{\mathrm{in}, j}^{k} \delta\left(\mathbf{x}^{\prime \prime}\right) \mathrm{d} \mathbf{x}^{\prime \prime} \\ & =\sum_{j=1}^{N} \mathbf{W}^{\ell k}\left(\mathbf{x}_{j}-\mathbf{x}_{i}\right) \mathbf{f}_{\mathrm{in}, j}^{k} \end{aligned} \] 这一卷积操作将type-k的向量映射为type-\(\ell\)的向量。
上述定义的卷积公式需满足等变性: \[ \begin{aligned} \mathbf{D}_{\ell}(g) \mathbf{f}_{\mathrm{out}, \mathrm{i}}^{\ell} & =\sum_{j=1}^{N} \mathbf{W}^{\ell k}\left(\mathbf{R}_{g}^{-1}\left(\mathbf{x}_{j}-\mathbf{x}_{i}\right)\right) \mathbf{D}_{k}(g) \mathbf{f}_{\mathrm{in}, j}^{k} \\ \Longrightarrow \mathbf{f}_{\mathrm{out}, \mathrm{i}}^{\ell} & =\sum_{j=1}^{N} \mathbf{D}_{\ell}(g)^{-1} \mathbf{W}^{\ell k}\left(\mathbf{R}_{g}^{-1}\left(\mathbf{x}_{j}-\mathbf{x}_{i}\right)\right) \mathbf{D}_{k}(g) \mathbf{f}_{\mathrm{in}, j}^{k} \end{aligned} \] 两式应该相等,因此从中可以推出: \[ \mathbf{W}^{\ell k}(\mathbf{R}_{g}^{-1}\mathbf{x})=\mathbf{D}_{\ell}(g)\mathbf{W}^{\ell k}(\mathbf{x})\mathbf{D}_{k}(g)^{-1} \] 这一公式为矩阵形式,可以通过重排改写为向量形式: \[ \mathrm{vec}(\mathbf{W}^{\ell k}(\mathbf{R}_g^{-1}\mathbf{x}))=(\mathbf{D}_k(g)\otimes\mathbf{D}_\ell(g))\mathrm{vec}(\mathbf{W}^{\ell k}(\mathbf{x})) \] 其中的张量积可以用Clebsch-Gordan分解来替换: \[ \mathrm{vec}(\mathbf{W}^{\ell k}(\mathbf{R}_g^{-1}\mathbf{x}))=\mathbf{Q}^{\ell k\top}\left[\bigoplus\limits_{J=|k-\ell|}^{k+\ell}\mathbf{D}_J(g)\right]\mathbf{Q}^{\ell k}\mathrm{vec}(\mathbf{W}^{\ell k}(\mathbf{x})) \] 简便起见,定义\(\eta^{\ell k}(\mathbf{x})\triangleq\mathbf{Q}^{\ell k}\mathrm{vec}(\mathbf{W}^{\ell k}(\mathbf{x}))\),从而有 \[ \eta^{\ell k}(\mathbf{R}_{g}^{-1}\mathbf{x})=\left[\bigoplus_{J=|k-\ell|}^{k+\ell}\mathbf{D}_{J}(g)\right]\eta^{\ell k}(\mathbf{x}) \] 其中的第\(J\)个子向量\(\eta^{\ell k}_J(\mathbf{x})\)满足约束条件\(\eta_{J}^{\ell k}(\mathbf{R}_{g}^{-1}\mathbf{x})=\mathbf{D}_{J}(g)\eta_{J}^{\ell k}(\mathbf{x})\),这正与球谐函数的变换法则\(\mathbf{Y}_{J}\left(\mathbf{R}_{g}^{-1} \mathbf{x}\right)=\mathbf{D}_{J}^{*}(g) \mathbf{Y}_{J}(\mathbf{x})\)相同。因此可以令\(\eta^{\ell k}_J(\mathbf{x})=\mathbf{Y}_J(\mathbf{x})\),从而得到权重矩阵\(\boldsymbol{W}^{\ell k}\)的构造: \[ \operatorname{vec}\left(\mathbf{W}^{\ell k}(\mathbf{x})\right)=\mathbf{Q}^{\ell k\top}\bigoplus\limits_{J=|k-\ell|}^{k+\ell}\mathbf{Y}_J(\mathbf{x}) \] 上面构造的这个权重矩阵中不包含可学习参数,此外这样的构造方式也只考虑了角度方向而没有考虑径向,因此可以加入一个可学习的径向函数\(\varphi_J^{\ell k}:\mathbb{R}_{\ge 0}\rightarrow \mathbb{R}\),从而有: \[ \operatorname{vec}\left(\mathbf{W}^{\ell k}(\mathbf{x})\right)=\mathbf{Q}^{\ell k\top}\bigoplus\limits_{J=|k-\ell|}^{k+\ell}\varphi_J^{\ell k}(\|\mathbf{x}\|)\mathbf{Y}_J(\mathbf{x}) \] 向量化的权重矩阵重新恢复为矩阵形式为: \[ \mathbf{W}^{\ell k}(\mathbf{x})=\sum_{J=|k-\ell|}^{k+\ell}\varphi_{J}^{\ell k}(\|\mathbf{x}\|)\sum\limits_{m=-J}^{J}\mathbf{Q}_{Jm}^{\ell k\top}Y_{Jm}(\mathbf{x})\\ \]
实验结果
作者分别在三个不同的任务上对模型做了测试,包括N体模拟,点云分类和分子化学性质预测。
在N体模拟任务中,\(SE(3)\)-transformer相比于没有加入等变约束的set transformer能够取得更好的结果,对于位置和速度的预测能够体现出等变性(图中的虚线代表旋转之后的正确位置):
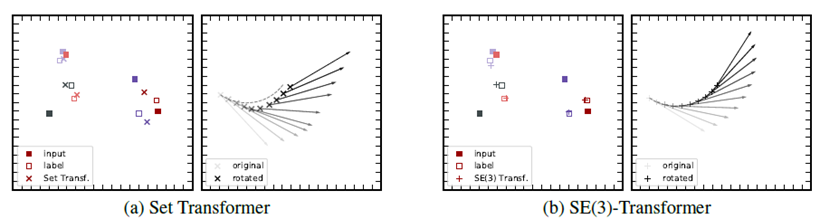
从定量结果上也可以看出\(SE(3)\)-transformer具有更高的精确度:
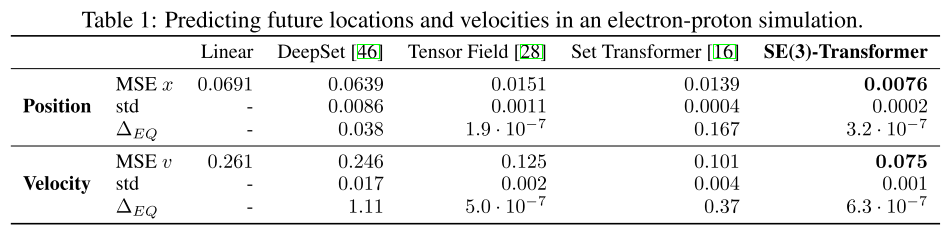
在点云数据集上有着类似的表现,模型的准确度也不会随着数据的旋转而发生下降,此处不再赘述。
在QM9数据集上模型的表现如下:
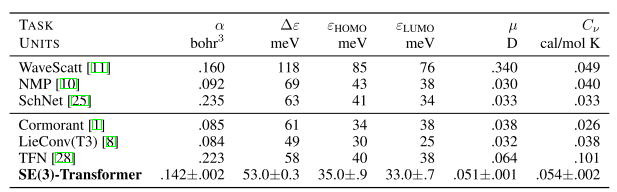
从中可以看出,\(SE(3)\)-transformer的结果并不是SOTA,但是误差与表现最好的模型相比差距并不很大,这也能一定程度说明模型较广的适用范围。
LieConv
概述
LieConv出自Generalizing Convolutional Neural Networks for Equivariance to Lie Groups on Arbitrary Continuous Data这一工作,它定义了李群上的卷积操作,从而可以实现任意李群上的等变网络。
模型的结构如下图所示:

其中,Lifting和LieConv是模型中的两个关键模块,下面将详细介绍。
Lifting操作
Lifting操作的定义为\(\text{Lift}(\boldsymbol{x})=\{\boldsymbol{u}\in G, \boldsymbol{uo}=\boldsymbol{x}\}\),用于将输入\(\boldsymbol{x}_i\)变换为群元素\(\boldsymbol{u}_i\),之后便可以做李群上的卷积操作。它的具体流程如下:

设输入为\(\{(\boldsymbol{x}_i,\boldsymbol{f}_i)\}_{i=1}^N\),其中\(\boldsymbol{x}_i\in\mathcal{X}\),对\(\boldsymbol{x}_i\)做变换的流程可以总结为三步:
为每个轨道\(q\in \mathcal{X}/G\)选择一个原点\(o_q\)。这里的轨道指的是\(\boldsymbol{x}\)所对应的空间\(\mathcal{X}\)与群\(G\)的商空间\(\mathcal{X}/G\),因此轨道可能只有一个或者可能有多个。下图分别为\(SO(2)\)群和\(T(1)y\)群所对应的轨道示意图:
![image-20230213112422440]()
为每个原点\(o_q\)计算集合\(H_q\),它被称作stabilizer,其中的元素满足\(H=\{h\in G,ho=o\}\)。
在完成上面两步之后,就可以为输入\(\boldsymbol{x}_i\)计算lifting之后的结果:
- 首先计算出\(\boldsymbol{x}_i\)所在的轨道\(q_i\)
- 然后从\(H_{q_i}\)中按照哈尔测度(一种定义在拓扑群上的测度)采样\(K\)个样本构成集合\(\{\boldsymbol{v}_j\}_{j=1}^K, \boldsymbol{v}_j\sim \mu(H_{q_i})\)
- 之后根据公式\(\boldsymbol{u}_i\boldsymbol{o}_q=\boldsymbol{x}_i\)得到群中的元素\(\boldsymbol{u}_i\in G\)
由此便可得到lifting之后的数据\(Z_i=\{(\boldsymbol{u}_i\boldsymbol{v}_j,q_i,\boldsymbol{f}_i)\}_{j=1}^K\)。
下图给出了几个不同群上面做lifting操作的示例:
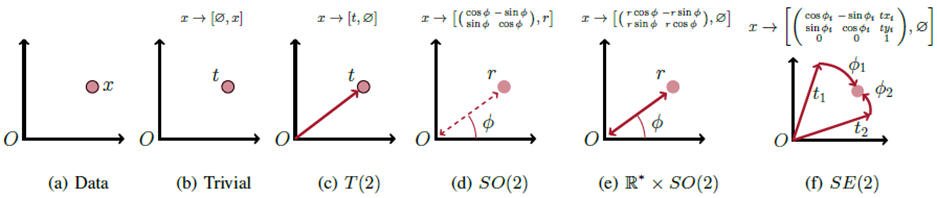
LieConv操作
设计在李群上卷积的计算步骤如下:

卷积操作主要包括三步:
首先寻找点\(i\)的所有近邻点,即满足\(d((\boldsymbol{u}_i,q_i),(\boldsymbol{u}_j,q_j))<r\)的所有点。这里距离的定义为: \[ d((\boldsymbol{u}_i,{q}_i),(\boldsymbol{u}_j,{q}_j))^2=\|\log (\boldsymbol{u}_i^{-1}\boldsymbol{u}_j)\|_F+\alpha\|q_i-q_j\| \] 如果lifting之后的数据不包含轨道,则其中含\(q\)的项可以省略。
计算向量\(\boldsymbol{a}_{ij}\),它被用于下一步的卷积计算。
计算卷积之后的结果。在连续空间中卷积的计算公式为: \[ h(\boldsymbol{u},q)=\int_{G,Q}k(\boldsymbol{v}^{-1}\boldsymbol{u},q,q')f(\boldsymbol{v},q')d\mu(\boldsymbol{v})dq' \] 将其离散化之后便有: \[ h_i=\frac{1}{n_i}\sum\limits_{j\in\text{nbd(i)}}\tilde{k}_\theta(\log(\boldsymbol{v}_j^{-1}\boldsymbol{u}_i),q_i,q_j)f_j=\frac{1}{n_i}\sum\limits_{j\in\text{nbd(i)}}\tilde{k}_\theta(\boldsymbol{a}_{ij})f_j \] 其中\(\tilde{k}_{\theta}\)是一个可学习的MLP。
需要注意的是,这里的卷积操作不是严格意义上的等变,而是依概率分布成立: \[ \begin{aligned} (k\hat{\ast}L_{w}f)(u_{i})&=(1/n_{i})\sum_{j}k(v_{j}^{-1}u_{i})f(w^{-1}v_{j})\\ &=(1/n_{i})\sum_{j}k(\tilde{v}_{j}^{-1}w^{-1}u_{i})f(\tilde{v}_{j})\\ &\stackrel{d}{=}(k\hat{\ast}f)(w^{-1}u_{i})=L_{w}(k\hat{\ast}f)(u_{i}) \end{aligned} \]
实验结果
作者分别在RotMNIST旋转手写数字分类,QM9分子性质预测,以及动力系统的轨迹预测三个任务上对模型的效果进行试验。
在旋转手写数字分类任务上,模型的结果如下:

其结果比较接近最好的baseline。
在分子性质预测任务上的表现:

结果与另外三个baseline模型也都比较接近。
在动力系统轨迹预测任务中,模型所预测的轨迹能够很好地与真实轨迹重合:
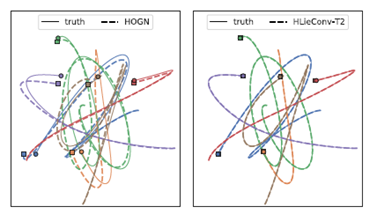
此外,选择不同的李群也让模型能够控制对哪些物理量保持守恒。例如使用\(SE(2)\)群就可以让角动量与线动量同时具有等变性,而使用\(T(2)\)则只能保持线动量的等变,使用\(SO(2)\)只能使模型保持角动量的等变:
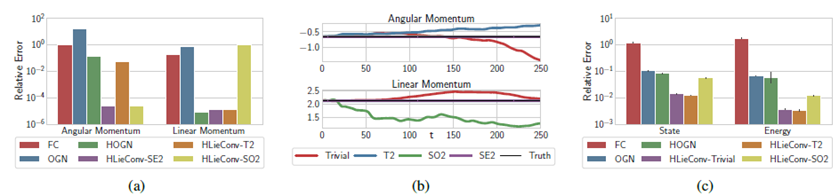
虽然LieConv模型无法在所有任务上取得SOTA的结果,但是在几个不同领域的任务上都能取得不错的结果,这也能说明模型的通用性。
EGNN
概述
E(n) Equivariant Graph Neural Networks通过使用向量的标量化操作来实现\(E(3)\)等变性。这一网络结构简单高效,目前在许多任务上都经常被用作Backbone。
网络结构
模型的输入包括结点的嵌入向量\(\mathbf{h}^{l}=\left\{\mathbf{h}_{0}^{l},\ldots,\mathbf{h}_{M-1}^{l}\right\}\),每个结点的坐标向量\(\mathbf{x}^{l}=\{\mathbf{x}_{0}^{l},\ldots,\mathbf{x}_{M-1}^{l}\}\)和边的特征向量\(\boldsymbol{e}_{ij}\)。EGNN基于如下的消息传递和特征聚合更新操作来做图卷积运算: \[ \begin{aligned} \mathbf{m}_{ij}&=\phi_x\left(\mathbf{h}_i^l,\mathbf{h}_j^l,\left\|\mathbf{x}_i^l-\mathbf{x}_j^l\right\|^2,\mathbf{e}_{ij}\right)\\ \mathbf{x}_i^{l+1}&=\mathbf{x}_i^l+\sum_j\left(\mathbf{x}_i^l-\mathbf{x}_j^l\right)\phi_x\left(\mathbf{m}_{ij}\right)\\ \mathbf{m}_i&=\sum_{j\in\mathcal{N}(i)}\mathbf{m}_{ij}\\ \mathbf{h}_i^{l+1}&=\phi_i\left(\mathbf{h}_i^l,\mathbf{m}_i\right) \end{aligned} \] 此外还有一个引入动量的拓展版本,坐标向量\(\boldsymbol{x}\)将使用一个额外的动量项\(\boldsymbol{v}\)做间接地更新: \[ \begin{array}{l}\mathbf{v}_{i}^{l+1}=\phi_{v}\left(\mathbf{u}_{i}^{l}\right)\mathbf{v}_{i}^{l}+\sum_{j\neq i}\left(\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}\right)\phi_{x}\left(\mathbf{m}_{ij}\right)\\ \mathbf{x}_{i}^{l+1}=\mathbf{x}_{i}^{l}+\mathbf{v}_{i}^{l+1}\end{array} \] 这一模型等变性的证明比较简单。首先可以证明消息\(\mathbf{m}_{ij}\)具有不变性: \[ \mathbf{m}_{i,j}=\phi_e\left(\mathbf{h}_i^l,\mathbf{h}_j^l,\left\|Q\mathbf{x}_i^l+g-[Q\mathbf{x}_j^l+g]\right\|^2,\mathbf{e}_{ij}\right)=\phi_e\left(\mathbf{h}_i^l,\mathbf{h}_j^l,\left\|\mathbf{x}_i^l-\mathbf{x}_j^l\right\|^2,\mathbf{e}_{ij}\right) \] 基于此便可以证明\(\boldsymbol{x}\)和\(\mathbf{v}\)的等变性: \[ \begin{aligned} &Q\mathbf{x}_{i}^{l}+g+\sum_{j\neq i}\left(Q \mathbf{x}_{i}^{l}+g-Q \mathbf{x}_{j}^{l}-g\right)\phi_{x}\left(\mathbf{m}_{i,j}\right) \\ =&Q x_{i}^{l}+g+Q\sum_{j\neq i}\left(\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}\right)\phi_{x}\left(\mathbf{m}_{i,j}\right)\\ =&Q\left(\mathbf{x}_{i}^{l}+\sum_{j\neq i}\left(\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}\right)\phi_{x}\left(\mathbf{m}_{i,j}\right)\right)+g\\ =&Q \mathbf{x}_{i}^{l+1}+g\end{aligned} \]
\[ \begin{aligned} &\phi_{v}\left(\mathbf{h}_{i}^{l}\right)Q \mathbf{v}_{i}^{l}+\sum_{j\neq i}\left(Q \mathbf{x}_{i}^{l}+g-[Q \mathbf{x}_{j}^{l}+g]\right)\phi_{x}\left(\mathbf{m}_{ij}\right) \\ =&{Q}\phi_{v}\left(\mathbf{h}_{i}^{l}\right)\mathbf{v}_{i}^l+{Q}\sum_{j\neq i}\left(\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}\right)\phi_{x}\left(\mathbf{m}_{ij}\right)\\ =&Q\left(\phi_{v}\left(\mathbf{h}_{i}^{l}\right)\mathbf{v}_{i}^l+\sum_{j\neq i}\left(\mathbf{x}_{i}^{l}-\mathbf{x}_{j}^{l}\right)\phi_{x}\left(\mathbf{m}_{ij}\right)\right)\\ =&Q \mathbf{v}_{i}^{l+1} \end{aligned} \]
各个特征在变换过程中的等变性和不变性如下图所示:

实验结果
作者分别在图自编码器,N体模拟和分子性质预测三个任务上面进行实验,下面为它们的结果:



从中可以看出,EGNN模型在不同的任务上面都能取得很好的结果,甚至在一些任务上面能够达到SOTA。
GNN与分子性质预测
下文为一些分子性质预测任务中一些比较具有代表性的GNN结构。早期的工作例如SchNet主要是从分子能量不变性以及原子力等变性的角度出发,使用标量法来设计网络结构,在此之后也有了一系列的改进工作。
SchNet
概述
对于卷积神经网络来说,它处理的是网格化的数据,但是对于分子中的原子来说,它们的位置并不是局限在某个格子内。此外,由于原子的准确位置也包含了重要的物理信息,如果只是简单地将距离离散化,则会丢失掉一些信息。因此,作者构造了SchNet这一图神经网络结构,并且在图卷积操作中使用了连续滤波卷积层(Continuous-filter Convolutional Layers),从而使得图卷积操作可以处理连续变化的数据。
Continuous-filter Convolution
对于原子位置数据,它们的数据类型是连续型的。虽然也可以将这些数据离散化,然后使用离散形式的卷积操作,但是如果要求较高的预测精度则需要使得网格尽量细密。而且更致命的是,离散卷积会导致模型输出的预测值也是离散的。下图所示为使用离散卷积与连续卷积所预测出原子能量变化曲线的示意图:

因此,作者提出了Continuous-filter convolutional操作。给定\(n\)个原子的特征\(X^l=(\boldsymbol{x}_1^l,\dots,\boldsymbol{x}_n^l)\),其中\(\boldsymbol{x}_i^l\in \mathbb{R}^F\)。它们的位置信息为\(\boldsymbol{R}=(\boldsymbol{r}_1,\dots,\boldsymbol{r}_n)\),其中\(\boldsymbol{r}_i\in \mathbb{R}^D\)。第\(l\)层的Continuous-filter Convolution操作需要一个filter-generating函数\(W^l:\mathbb{R}^D \rightarrow \mathbb{R}^F\),它将连续形式的位置信息映射为对应的filter value。
在位置\(\boldsymbol{r}_i\)处的Continuous-filter Convolution的计算公式如下: \[ \boldsymbol{x}_i^{l+1}=(X^l * W^l)_i=\sum_{j} \boldsymbol{x}_j^l \circ W^l(\boldsymbol{r}_i-\boldsymbol{r}_j) \] 其中\(\circ\)代表逐元素相乘,这种计算方式可以提高计算效率。
网络结构
SchNet的设计目标是用来预测分子的能量以及其中每个原子的作用力,因此它的网络结构设计能够满足一些基础的物理规则,例如原子序号、平移、旋转不变性,获得连续变化的能量预测值,以及能量守恒的力场。它的网络结构如下图所示:

输入:网络的输入为分子表征,即\(n\)个原子的原子序数\(Z=(Z_1,\dots,Z_n)\)以及它们的位置\(R=(\boldsymbol{r}_1,\dots,\boldsymbol{r}_n)\)。而在网络的隐藏层中,原子的特征被表示为特征向量的形式,即\(X^l=(\boldsymbol{x}_1^l,\dots,\boldsymbol{x}_n^l)\)。而特征向量的初始化是通过embedding层来完成的,每个原子序数都对应于一个嵌入向量,即\(\boldsymbol{x}_i^0=\boldsymbol{a}_{Z_i}\)。
激活函数:作者在构造损失函数时,使用了能量与力的联合损失函数,因此要求模型至少二阶可导。为了满足这一条件,作者使用了Shifted softplus函数:\(ssp(x)=\ln (0.5e^x+0.5)\)
Atom-wise层:Atom-wise层其实就是一个全连接层,每个原子的特征向量都进行如下的特征变换:\(\boldsymbol{x}_i^{l+1}=W^l\boldsymbol{x}_i^n+b^l\)。由于这些权重系数是所有原子共享的,因此这一网络适用于不同大小的分子。
Interaction模块:这一模块的主要作用是使用分子的位置信息来更新结点的向量表示。其中使用了残差模块,这使得原子之间的相互作用以及原子自身的特征可以更加灵活地进行组合。
cfconv层:cfconv层包含了图卷积操作以及filter-generating网络。为了满足旋转不变性,在构造函数\(W^l\)的时候使用了原子之间的距离。作者提到,如果直接使用距离的标量数值,那么不同层的过滤器将会高度相关,因为初始状态的神经网络接近于线性(为什么?),这将会导致网络难以优化。为了避免这种情况的出现,作者使用了RBF函数对距离的值进行处理,将其扩展为一个向量: \[ e_k(\boldsymbol{r}_i-\boldsymbol{r}_j)=\exp(-\gamma ||d_{ij}-\mu_k||^2) \] 通过手动加入非线性,使得过滤器之间的相关性减小。在使用ethanol的分子动力学轨迹数据训练模型之后,三个interaction模块产生的过滤器在二维平面上的可视化效果如下图所示,其中蓝色代表负值,红色代表正值。从中可以看到,每个过滤器只关注特定范围内的原子距离。
![image-20210811213815132]()
损失函数
网络训练过程中使用的损失函数是能量和力的联合损失函数: \[ L=\rho ||E-\hat{E}||^2 +\frac{1}{n}\sum_{i=0}^n ||\boldsymbol{F}_i-\hat{\boldsymbol{F}}_i||^2 \] 其中, \[ \hat{\boldsymbol{F}}_i(Z_1,\dots,Z_n,\boldsymbol{r}_1,\dots,\boldsymbol{r}_n)=-\frac{\partial \hat{E}}{\partial \boldsymbol{r}_i}\left(Z_1,\dots,Z_n,\boldsymbol{r}_1,\dots,\boldsymbol{r}_n \right) \]
备注:如果使用PyTorch训练SchNet的话,力的计算可以使用
torch.autograd.grad函数方便地求得。
实验结果
作者使用QM9、MD17和ISO17三个不同的数据集对SchNet进行训练。其中QM9只包含了平衡态的分子结构,MD17包含了一个分子的分子动力学模拟演化,ISO17同时包含了结构变化和化学变化。结果如下:
- 作者比较了DTNN、enn-s2s以及SchNet这三个网络在QM9数据集上的能量预测误差(MAE),从中可以看出,SchNet的表现是三者中最好的:

在MD17数据集上,作者将训练结果与GDML和DTNN两个网络进行对比。由于GDML无法在大规模数据集上训练,因此作者使用小规模数据集同时训练SchNet和GDML。在小规模的数据集上,GDML的表现总体优于SchNet。
而如果单从SchNet的训练结果来看,如果在训练过程中只使用能量的数据,那么训练效果并不好,能量和力的误差都较高;但是如果使用能量与力的联合误差,那么能量和力的预测精度都会提升。
![image-20210811225124541]()
在ISO17数据集中,包括了129种化学式为\(C_7O_2H_{10}\)的同分异构体的分子动力学轨迹数据。从模型的预测误差中可以看出,在预测已知分子结构的未知构象(即化学键相同,但是原子的空间位置排布方式不同)时,模型的预测效果较好;但是当遇到分子结构和构象都未知的情况下,预测误差会显著上升。

总结
本文提出了Continuous-filter convolution这一新的图卷积运算,使其能够使用连续型的数据直接进行运算,并基于这一图卷积运算提出了SchNet网络结构。SchNet网络结构能够满足如平移不变性、旋转不变性等物理规则,在量子化学的任务上取得了很好的效果。此外,通过构造能量与力的联合损失函数,在分子动力学轨迹数据集上也取得了精确的预测结果。
但是这一结构也具有一定的局限性,比如它无法区分下面的两个图:
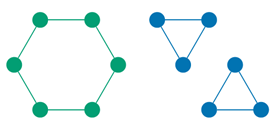
DimeNet
概述
Directional Message Passing for Molecular Graphs是来自于ICLR2020的一篇文章。在这篇文章中,作者提到之前的一些图神经网络在预测分子性质的时候只使用到了原子之间的距离信息,但是却没有考虑原子之间的空间方向信息。但是在一些分子的经验势函数中,原子之间的角度信息却起着关键作用。因此,作者基于MPNN框架设计了DimeNet网络结构,在信息传递过程中加入了角度信息。此外,作者还使用了球贝塞尔函数(可参考球贝塞尔函数)和球谐函数(可参考球谐函数介绍)来代替广泛使用的高斯径向基函数,这样可以使用更少的参数量取得更好的效果。
设计思路
输入和输出
作者设计的DimeNet主要是为了做回归任务,即预测连续型的分子性质,如势能、偶极矩、毒性等。网络的输入仅为原子序数\(\boldsymbol{z}=\{z_1,\dots,z_n\}\)和原子的位置\(\boldsymbol{X}=\{\boldsymbol{x}_1,\dots,\boldsymbol{x}_n\}\),输入为一个实数域上的标量,因此网络可以简单地表示为函数\(f_{\theta}:\{\boldsymbol{X},\boldsymbol{z}\}\rightarrow \mathbb{R}\)。一些模型额外加入了辅助特征例如化学键类型、原子的电负性等特征,但是作者认为这些信息并不是必要的。此外,如果要将DimeNet作为势函数来使用,则要求网络结构对应的函数满足二阶连续可微的条件,这些辅助特征的加入无法使得网络结构满足这一条件。
角度信息
传统分子势函数的经验公式可以表示为四个部分的和: \[ E=E_{\text{bond}}+E_{\text{angle}}+E_{\text{torsion}}+E_{\text{non-bonded}} \] 对于没有加入角度信息的图神经网络来说,上述四个组成部分中缺少了\(E_{\text{angle}}+E_{\text{torsion}}\)这两个部分。因此作者提出,加入角度信息是很有必要的。此外,如果没有角度信息,则无法对一些分子结构进行区分,例如苯环结构对应的图结构和两个环丙烷组成的图结构。从这一点来看,引入角度信息就可以解决这一问题。
此外,为了降低计算量,需要引入截断半径,只在一个原子的局部范围内做图卷积运算。
带方向的消息传递
对于分子性质预测任务来说,图卷积操作需要满足平移不变性、旋转不变性、奇偶对称性,以及网络的输出应当与原子的排列顺序无关。因此作者构造的消息传递函数如下: \[ \boldsymbol{m}_{ji}^{(l+1)}=f_{\text{update}}\left(\boldsymbol{m}_{ji}^{(l)},\sum_{k\in N(j)\backslash \{i\}} f_{\text{int}}(\boldsymbol{m}_{kj}^{(l)},\boldsymbol{e}_{\text{RBF}}^{(ji)},\boldsymbol{a}_{\text{SBF}}^{(kj,ji)}) \right) \] 上述公式其实相当于是两次消息传递过程的叠加。消息更新过程使用简单的加和即可,即\(\boldsymbol{h}_i^{(l+1)}=\sum_{j}\boldsymbol{m}_{ji}^{(l+1)}\)。这一过程可以表示为下图:
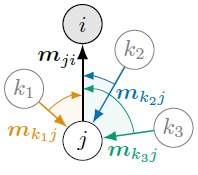
其中,\(\boldsymbol{e}_{\text{RBF}}^{(ji)}\)是结点之间距离\(d_{ji}\)经过径向基函数的转换而得到的一个长度为\(N_{\text{RBF}}\)的向量,每个元素通过下面的公式计算而得: \[ e_{\text{RBF,n}}(d)=u(d)\sqrt{\frac{2}{c}}\frac{\sin (\frac{n\pi}{c}d)}{d} \] 上式中的\(n\in[1,2,\dots,N_{\text{RBF}}]\),\(c\)代表截断半径。
而\(\boldsymbol{a}_{\text{SBF}}^{(kj,ji)}\)则指的是结点之间距离\(d_{kj}\)和结点\(i,j,k\)的角度\(\alpha_{(kj,ji)}\)经过贝塞尔基函数计算得到的一个长度为\(N_{\text{SRBF}}*N_{\text{SHBF}}\)向量,其中每个元素的计算公式如下: \[ a_{\text{SBF,ln}}(d,\alpha)=u(d)\sqrt{\frac{2}{c^3 j_{l+1}^2(z_{ln})}}j_l(\frac{z_{ln}}{c}d)Y_l^0(\alpha) \] 上式中,\(l\in[0,1,\dots,N_{\text{SHBF}-1}]\),\(n\in[1,2,\dots,N_{\text{SRBF}}]\),\(c\)为截断半径,\(z_{ln}\)代表\(l\)阶贝塞尔函数的第\(n\)个根(可以通过数值计算的方法提前计算完成),\(j_l\)代表第一类球贝塞尔函数的第\(l\)项表达式,\(Y_l^0\)表示\(m=0\)的第\(l\)项球谐函数的表达式。这样构造的原因是考虑了定态薛定谔方程在三维无限深势阱内的球坐标解可以表示为\(\Psi(d,\alpha,\phi)=\sum_{l=0}^{\infty}\sum_{m=-l}^{l}(a_{lm}j_l(kd)+b_{lm}y_{l}(kd))Y_l^m(\alpha,\phi)\)。
RBF和SBF函数乘上\(u(d)\)是为了使它们能够在截断半径处连续地过渡到0,作者使用了如下的多项式函数: \[ u(d)=1-\frac{(p+1)(p+2)}{2}d^p+p(p+2)d^{p+1}-\frac{p(p-1)}{2}d^{p+2} \] 按照这种方式构造的消息传递操作可以满足平移不变性、旋转不变性、奇偶对称性的要求,且输出与原子的排列顺序无关。
网络结构
DimeNet的网络结构如下图所示。图中的\(\boldsymbol{W}\)和\(\boldsymbol{b}\)代表可学习参数,\(||\)代表向量的拼接操作,\(\odot\)代表逐元素相乘的操作,\(\sum\)代表累加操作,\(+\)代表逐元素相加,\(\sigma\)代表Swish激活函数\(\sigma(x)=x\cdot \text{sigmoid}(x)\)。
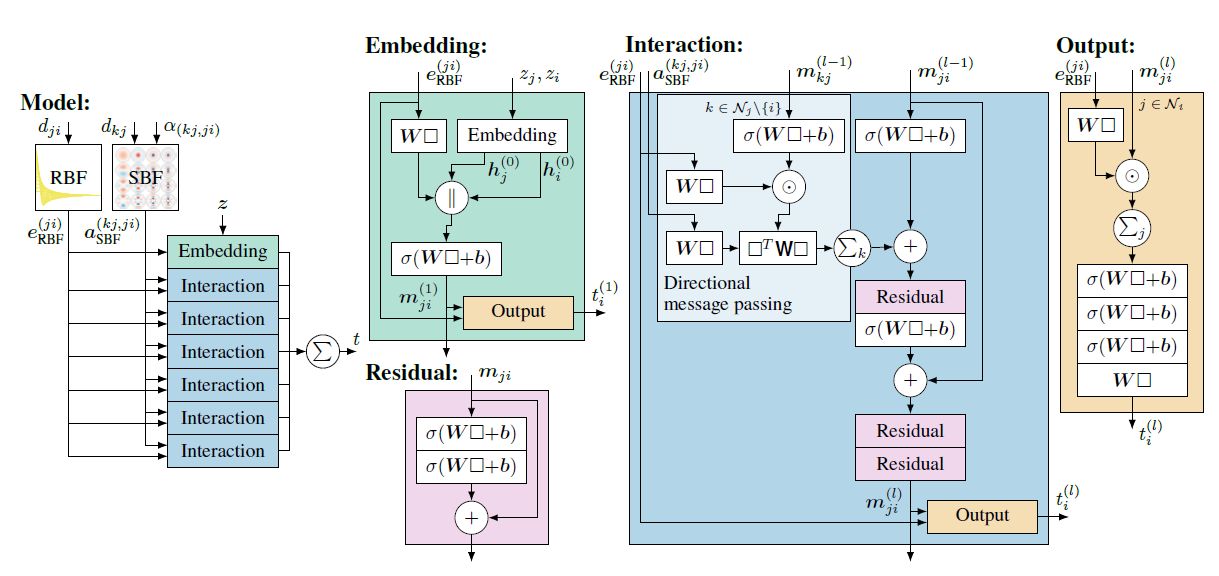
实验结果
DimeNet在QM9数据集上的表现如下表所示,其中每一个预测目标都对应于一个单独的模型:
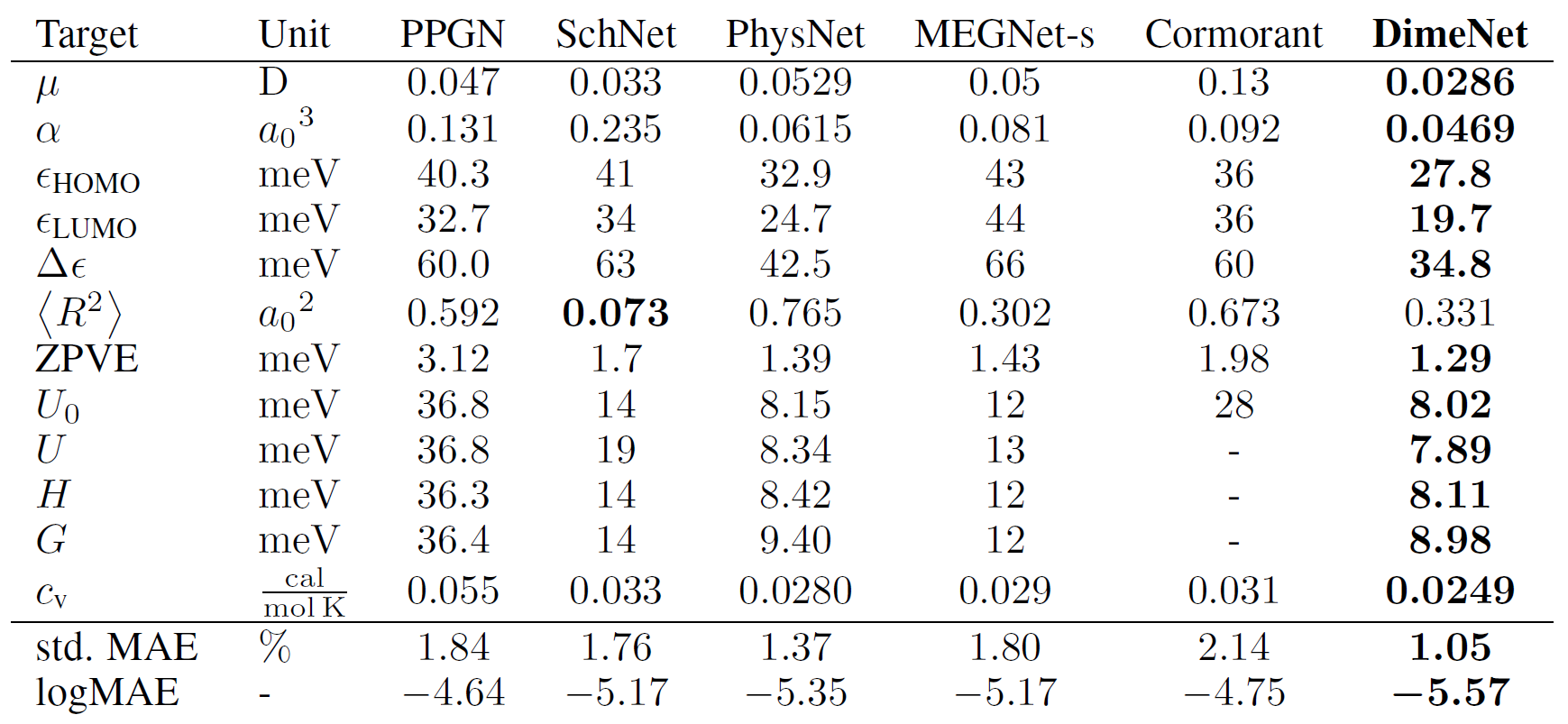
从中可以看到,相比于其它几个网络结构,DimeNet在大多数预测目标上面都能取得最好的效果。而且从平均绝对误差百分比来看,DimeNet比效果第二好的PhysNet要好31%。
在MD17数据集上,DimeNet的表现如下。需要注意的是,这一结果是通过仅使用1000个训练样本来训练模型得到的。

从中可以看出,DimeNet的预测误差率与sGDML比较接近,能够取得较好的精度。
改进
原始的DimeNet需要很大的计算开销,而且计算速度较慢,因此后面有了优化版的模型DimeNet++,它对原始的网络结构做了一些修改(其中红色部分为修改的地方):
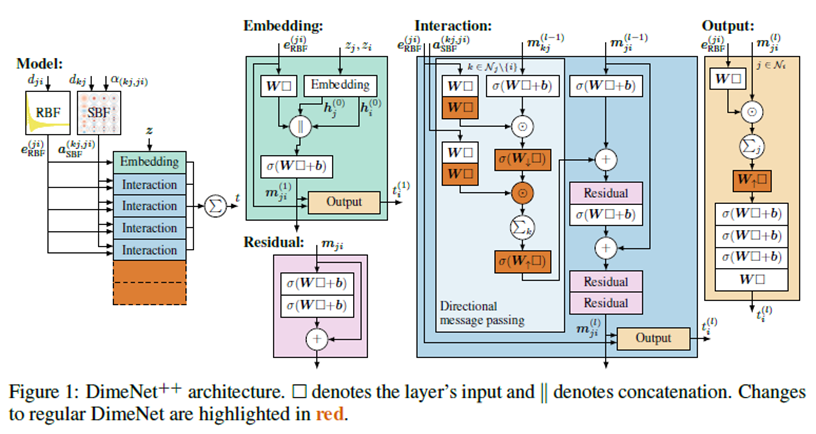
原始的DimeNet模型最耗时的在矩阵乘法\(\square^T \mathbf{W}\square\)这一步计算上,因此作者舍弃掉了这一步,将其修改为逐元素乘积,从而显著加快了速度。与此同时,模型的精度相比于原始模型也有了微弱的提升:

总结
DimeNet结构在消息传递的过程中引入了键角信息,从而使得在分子性质预测任务上能够取得更好的效果。但是这样仍然具有一定的局限性。例如DimeNet无法区分如下的两个分子:

此外,DimeNet也无法区分手性分子。
DimeNet虽然引入了键角信息,但消息传递过程仍然只是具有\(E(3)\)不变性。要解决上述的问题,则需要设计\(SE(3)\)不变的消息传递。或者另一种方法是引入具有\(E(3)\)等变性的特征(可以参考工作Equivariant message passing for the prediction of tensorial properties and molecular spectra),比如EGNN网络中使用的动量特征\(\mathbf{v}\),如下图所示:

GemNet
概述
GemNet这一工作在DimeNet的基础上,在消息传递过程中额外添加了二面角信息,从而实现了在消息传递过程中的\(SE(3)\)不变性,但是与此同时也使得模型的计算开销进一步增大。
网络结构
在消息传递过程中,作者定义了下图所示的两跳消息传递:
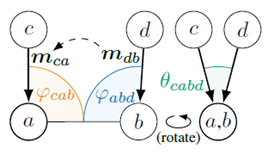
在两跳消息传递的过程中,以原子\(a\)为中心,计算原子\(c\)给原子\(a\)传递的消息\(\boldsymbol{m}_{ca}\)时,不仅要像DimeNet一样考虑\(a,c\)的直接作用关系,\(a\)的另一个邻居\(b\)再加上\(c\)所产生的\(a,b,c\)三者之间的作用关系,还要考虑\(b\)的邻居\(d\)所产生的\(a,b,c,d\)这四个原子之间的关系。
最终的消息传递表达式如下: \[ \tilde{\boldsymbol{m}}_{ca}=\sum_{b\in\mathcal{N}_{a}^\mathrm{int}\setminus\{c\},d\in \mathcal{N}_{b}^\mathrm{emb}\setminus\{a,c\}} \left((\mathbf{W}_{\mathrm{SBF1}}\mathbf{e}_{\mathrm{SBF}}(x_{ca},\varphi_{cab},\theta_{cabd}))^T\mathbf{W}((\mathbf{W}_{\mathrm{CBF2}}\mathbf{W}_{\mathrm{CBF1}}e_{\mathrm{CBF}}(x_{ba},\varphi_{abd})) \\ \odot(\boldsymbol{W}_{\mathrm{RBF2}}\boldsymbol{W}_{\mathrm{RBF1}}\boldsymbol{e}_{\mathrm{RBF}}(x_{db}))\odot\boldsymbol{m}_{db})\right) \] GemNet的网络结构如下图所示,与DimeNet有些类似之处:

其中RBF,CBF和SBF的定义如下: \[ \begin{aligned} \tilde{\mathbf{e}}_{\mathrm{RBF},n}(x_{d b})=&\sqrt{\frac{2}{c_{\mathrm{emb}}}}\frac{\sin(\frac{\pi\pi}{c_{\mathrm{emb}}}x_{d b})}{x_{d b}}\\ \tilde{\mathbf{e}}_{\mathrm{CBF};l n}(x_{b a},\varphi_{a b d})=&\sqrt{\frac{2}{c_{\mathrm{int}}^{3}j_{a}^{2}+1}(z_{l n})}j_{l}(\frac{z_{l n}}{c_{\mathrm{int}}}x_{b a})Y_{l0}(\varphi_{a b d})\\ \tilde{\mathbf{e}}_{\mathbf{SBF},l m n}(x_{c a},\varphi_{c a b},\theta_{c a b d})=&\sqrt{\frac{2}{c_{\mathrm{emb}}^{3}j_{l+1}^{2}(z_{l n})}}j_{l}(\frac{z_{l n}}{c_{\mathrm{emb}}}x_{c a})Y_{l m}(\varphi_{c a b},\theta_{c a b d}) \end{aligned} \] 这里的RBF和CBF定义与DimeNet中的RBF和SBF相同,而GemNet中的SBF则是以球谐函数作为基函数所计算出的特征向量。
实验结果
作者在MD17,COLL以及OC20数据集上分别做了实验。在实验结果中,GemNet-Q代表使用两跳的消息传递,GemNet-T代表只使用一跳的消息传递(类似DimeNet),后缀为dQ和dT的代表让模型直接预测原子力。
MD17数据集上的原子力的预测误差(MAE)如下表所示:
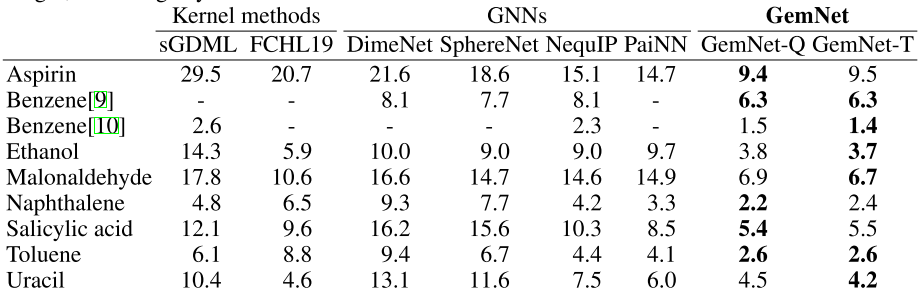
从中可以看出,GemNet比其它几种参与对比的网络结构有着更低的预测误差。同时也可以看到,使用两跳消息传递与一跳消息传递的预测误差十分接近。
在COLL数据集上的预测误差(MAE)如下表所示:
在这一数据集上的结果显示,两跳的消息传递能够取得更低的预测误差。此外,直接预测原子力的误差,相比于先预测能量然后再求导计算原子力的误差,也会更大一些。
在OC20数据集上的结果显示,GemNet相比于其它模型也有着更好的表现:

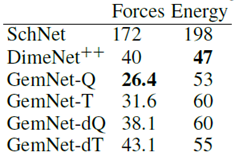
除此之外,作者也做了不同模型的运行时间对比:

将运行时间进行对比可以发现,模型训练过程中最耗时的模块为两跳的消息传递过程(Q和T相比)。此外如果对能量求导来计算力,然后再反向传播优化模型的过程也比较耗时(Q和dQ,T和dT相比)。而在推理阶段,最耗时的仍然为两跳的消息传播(Q和T相比)。
总结
GemNet这一工作设计了两跳的消息传递,使得模型的消息传递过程能够保持\(SE(3)\)不变性,在下游任务上面能够取得更好的结果。但是这样的设计也带来了更大的计算开销,在模型训练和推理阶段,相比于DimeNet这种一跳的消息传递,用时会有成倍的提升。



