引言
在分子性质预测任务中,有标签的数据通常十分宝贵。因此,目前有一些工作使用大规模无标签(或弱标签)数据集对模型做预训练,然后在下游任务上进行微调,从而提高在下游任务上的表现,下文将介绍其中的一些工作。本文具有一定的时效性,此外本文的内容以3D(即除了拓扑结构之外还包含有原子坐标信息)的分子为主。
基于特征预测的方法
Pretrain-GNN
简介
文章Strategies for Pre-training Graph Neural Networks(下文简称Pretrain-GNN)介绍了一种可以用于图神经网络预训练的策略,并通过分子性质预测以及蛋白质功能预测两个任务来证明这一手段的有效性。在后续的一些工作中,经常借鉴其中提出的一些预训练策略,并且提出的方法也常被用作自监督学习的benchmark之一。
预训练策略
在文章中,作者提出了四种不同的预训练策略,分为结点层级(Node-level)的预训练和图层级(Graph-level)的预训练。而在这两种不同层级的预训练中,又分为性质预测和结构预测两个任务。
结点层级预训练
在结点层级的预训练中,作者提出了两种方法,分别为Context Prediction和Attribute Masking,它们的原理可以表示为下图:
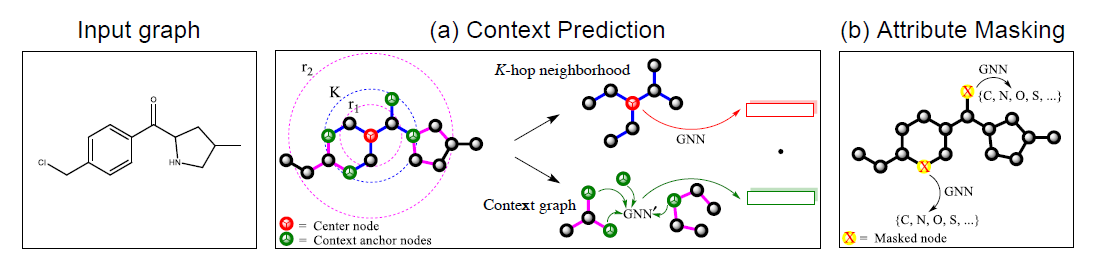
Context Prediction
为Context Prediction这一预训练任务设计的目标是,给定一个Subgraph以及一个Context graph,判断二者是否来自于同一图结构的同一结点。针对于结点\(v\),它的Subgraph被定义为它的K-hop Neighborhood,指的是与\(v\)的距离在\(K\)以内的所有结点和边;而它的Context graph则需要\(r_1\)和\(r_2\)两个参数,取与\(v\)的距离在\(r_1\)和\(r_2\)之间的所有边和结点构成一个子图,这可以理解为环绕\(v\)的邻居结点的子图结构。
为了使得Subgraph和Context graph中有一些结点共享,需要保证\(r_1<K<r_2\)。作者将这些共享的结点称为Context anchor nodes,它们的存在提供了两个子图如何连接在一起的信息。
这一预训练任务相当于是一个二分类问题,因此训练数据中需要同时有正负样本。正样本指的是Subgraph和Context graph来自于同一个结点,而负样本则刚好相反。在得到正样本之后,负样本的生成也很简单,针对于一个特定的Subgraph,只需要在与它不匹配的Context graph中随机选择一个即可。
在训练过程中,使用主GNN网络对Subgraph进行编码,得到一个固定长度的向量\(\boldsymbol{h}\);同时需要使用一个辅助GNN网络将Context graph编码为另一个固定长度的向量\(\boldsymbol{k}\)。然后计算\(\text{Sigmoid}(\boldsymbol{h}^T\boldsymbol{k})\),从而判断二者是否来自于同一个结点。在训练结束之后,只需要保留主GNN网络即可。
Attribute Masking
Attribute Masking这一训练任务的目标是从图结构中结点/边的分布规律中学习到一些相应的领域知识。这一预训练任务需要引入一个特殊的Mask变量,然后在图结构中随机选择若干个结点/边,将其设置为Mask。然后便可以使用GNN去学习结点和边的特征向量表示,其中包含了它周围的结构信息。以有机物分子图为例,可以将原子结点的元素种类遮盖起来,构造预测原子种类的预训练任务。
为了使用结点/边的特征向量去预测它被遮盖的特征,需要再引入一个模型(可以是线性模型等),这一模型以特征向量为输入,以结点/边自身的特征为输出。通过结点/边的真实特征和预测特征便可计算模型损失,对它做反向传播即可对网络的参数进行更新。
作者提到,这种预训练方法在结点信息充足的图结构中会取得很大的收益。例如在分子图中,结点信息对应于原子种类,GNN学习结点的分布规律的同时也可以学习到一些化学规则,例如化合价、官能团性质等信息;而在蛋白质的交联网络中,边的信息对应于两个蛋白质分子之间不同的相互作用,让GNN学习这些相互作用在图中的分布规律可以让GNN学习到不同相互作用之间的关联性。
图层级预训练
Property Prediction
为了将图层级的领域知识引入到预训练模型中,可以让模型去完成图的性质预测这一监督学习任务。具体地说,就是构造一个多目标学习的任务,让模型同时预测图的这些性质。例如在分子性质预测任务中,可以让模型去预测某个分子已知的所有性质(可参考QM9数据集)。
作者发现,如果仅仅是用多目标预测的预训练方式,可能无法生成可迁移的图层级表征。这是因为预训练中的一些任务可能与后续要完成的任务无关,甚至可能会起到反作用。一个解决办法是尽可能地选择与后续任务相关的预训练任务,但是这需要掌握一些领域知识。另一种解决办法是先进行结点层级的预训练,然后再做图层级的预训练。这是因为图层级的预训练可能无法产生有用的结点特征表示,而且不同的任务之间可能会相互影响。
Structural Similarity Prediction
另一个图层级的预训练方式是为两幅图的结构相似性建模。但是这种方式需要花费很大的工作量去构造数据集,因此作者仅仅是提出了这种方式,并未在实验过程中用到这一手段。
实验
为了验证上述预训练方法的效果,作者使用分子性质预测和蛋白质功能预测这两个化学和生物领域的任务进行实验。下面介绍实验的设计以及结果。
对于化学领域的任务,结点层级预训练使用的数据来自于ZINC15数据集中随机采样出的200万个分子结构;而图层级预训练使用的数据来自于ChEMBL数据集,其中包含了约45万个原子以及1300多种不同的性质。
对于生物领域的任务,结点层级预训练的数据集包含了从50个物种中的PPI网络中提取出来的约40万个蛋白质的ego-network;图层级的预训练数据集包含了8.8万个蛋白质的ego-network,以及它们粗粒度的生物学特性。
备注:ego-network的详细解释可参考自我中心网络-Egonetwork - 简书 (jianshu.com)
在预训练完成之后,化学领域的下游任务使用的是MoleculeNet这一工作中用到的数据集;而生物领域则依据Zitnik等人的工作构造出的PPI网络,从中提取出ego-network。
结果分析
下表为是否做预训练的不同网络结构在测试集上的ROC-AUC指标:

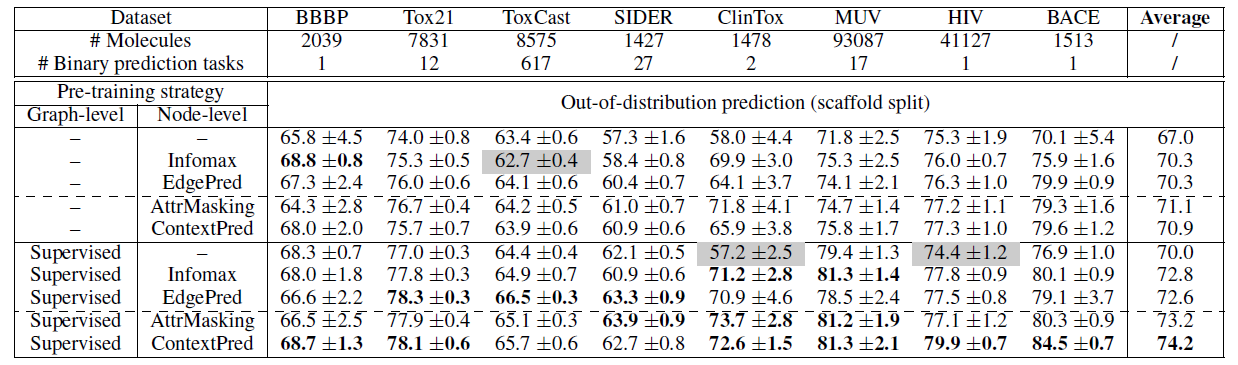
下表为GIN网络在使用不同的预训练方法组合时,化学领域任务上的表现。其中粗体代表预训练效果较好,而阴影组则代表预训练起了反作用:
下面的图表为生物领域上预训练的表现:
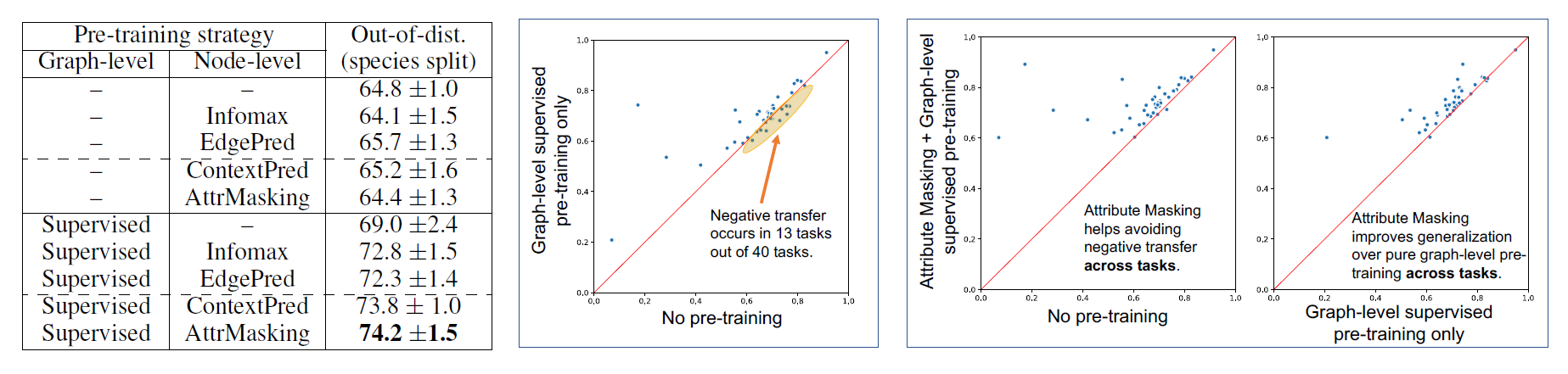
从这些实验结果中,可以得到的结论有:
- 预训练方法在表达能力更强的网络结构(如GIN)上可以取得更好的效果。但是在表达能力较弱的网络结构(如GCN、GraphSAGE、GAT等)上,预训练的提升效果不是很明显,甚至可能会起到反作用。
- 如果只做图层级的多任务监督学习预训练,对于网络预测效果的提升有限,甚至会产生反作用。
- 如果只做结点层级的预训练,对于网络的提升效果也有限
- 如果同时做结点层级和图层级的预训练,就不会出现负迁移的现象,并且可以取得最好的效果(同时也提升了相应任务的Baseline)
同时作者也发现,在使用预训练好的网络进行下游任务的学习时,ROC-AUC指标很快就可以达到一个比较高的值。而相比之下,没有做预训练的网络则花费很长时间也无法达到相同的数值。如下图所示(实线代表训练集,虚线代表验证集):
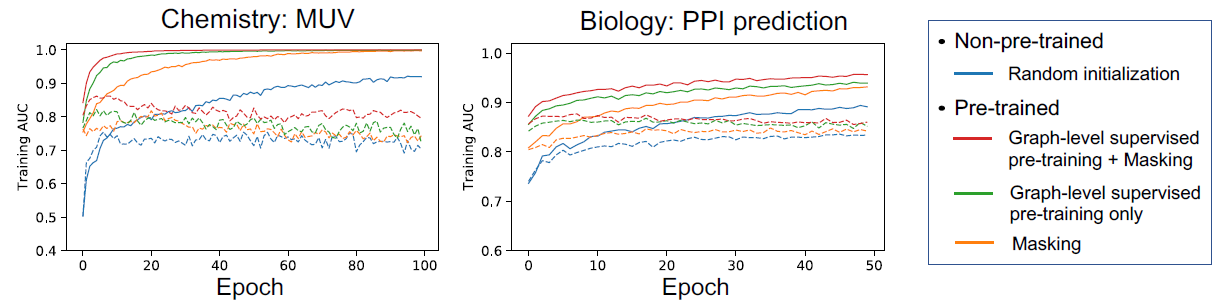
Chem-RL GEM
### 简介
ChemRL-GEM: Geometry Enhanced Molecular Representation Learning for Property Prediction这一工作提出了一个新的GNN结构GeoGNN,并提出了三种几何层级上的自监督学习任务。但是在下游任务上面的结果显示,这些自监督学习任务的帮助却并不太大。
几何层级自监督预训练
作者认为,一个分子的几何信息差异可以用于区别结构相近的分子,因此作者设计了三个不同的自监督学习任务:预测键长、预测键角、预测原子之间距离,如下图所示:
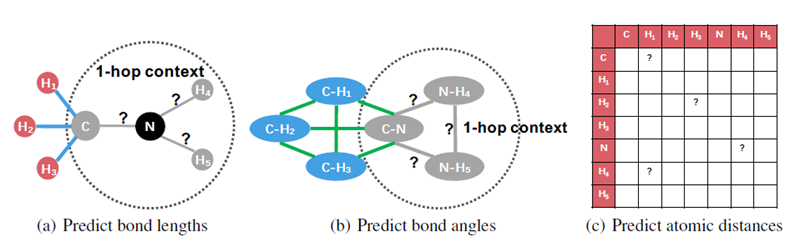
这三个自监督学习任务的损失函数分别为: \[ \begin{aligned} &L_{length}(\mathcal{E})=\frac{1}{|\mathcal{E}|}\sum_{(u,v)\in\mathcal{E}}(f_{length}(h^{(K_w},h^{(K_w)}_{v})-l_{uv})^2\\ &L_{angle}(\mathcal{A})=\frac{1}{|\mathcal{A}|}\sum_{(u,v,w)\in\mathcal{A}}(f_{angle}(h^{(K_w)},h^{(K_w)},h^{(K_w)}_{w})-\phi_{uvw})^2 \\ &L_{distance}(\mathcal{V})=\frac{1}{|\mathcal{V}|^{2}}\sum_{u,v\in\mathcal{V}}-bin^{T}(d_{u v})\cdot log(f_{distance}(h_{u}^{(K)},h_{v}^{(K)})) \end{aligned} \]
实验结果
下面是在几个回归和分类任务上面与其它预训练方法的比较:
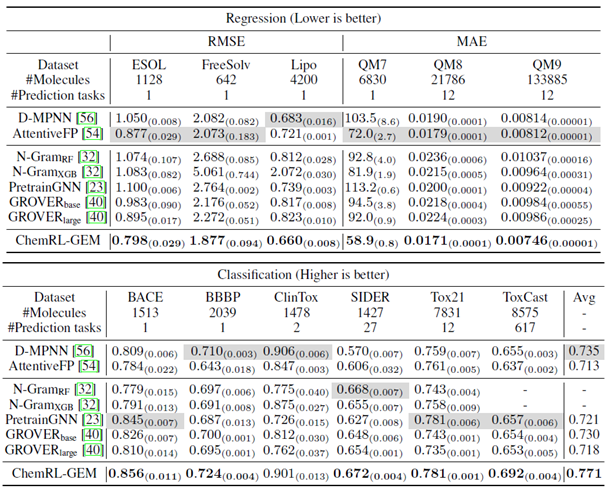
相比于表中其它的预训练方法,ChemRL-GEM的结果要稍好一些。
此外作者也做了消融实验:
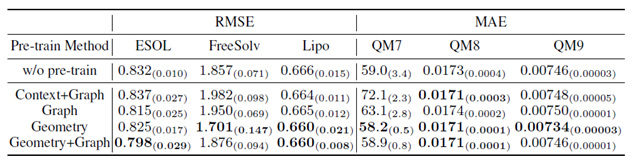
其中的Graph指的是预测分子指纹这一图层级的任务,Context指的是预测结点类型(即原子种类)这一结点层级的任务。
但是消融实验的结果显示,即使模型不做任何的预训练,它的表现并没有比加入预训练之后要差很多。这说明基于几何特征的预训练起到的效果比较微弱。因此在与其它预训练方法对比的时候,其效果优于其它几种方法很可能是因为模型设计的因素。
基于对比学习的方法
3D infomax
概述
3D Infomax这篇文章的主要思想是用一个分子的2D特征表示与3D特征表示做对比学习,期望2D的GNN所产生的特征向量中能够包含有一定的3D信息。在下游任务上,就可以直接用2D的GNN来做,这样比3D的GNN要快,同时也比不包含3D信息的GNN更加准确。整体思路表示为下图:
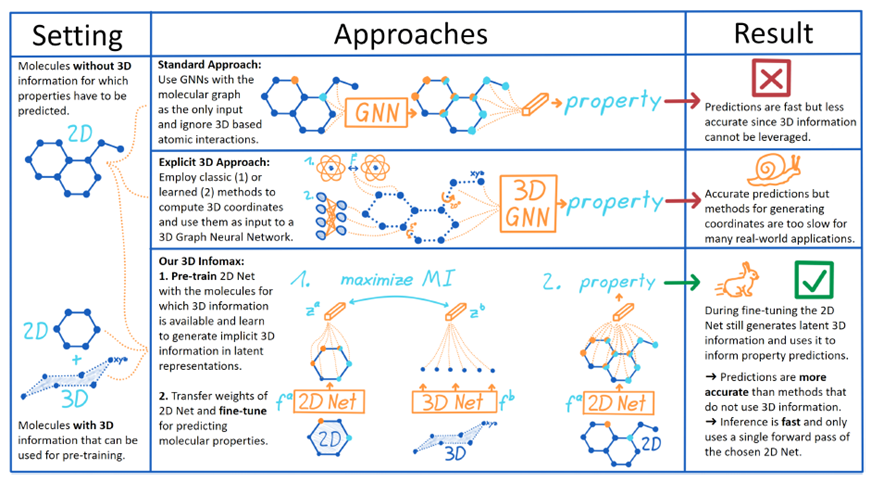
其中,2D Net是PNA,3D Net是SphereNet。
对比学习设计
由于一个2D分子可以对应于多个不同的3D构象,因此作者在设计对比学习任务时,认为一个2D分子与它所有的3D构象都是正类,其余为负类。可以表示为下图:
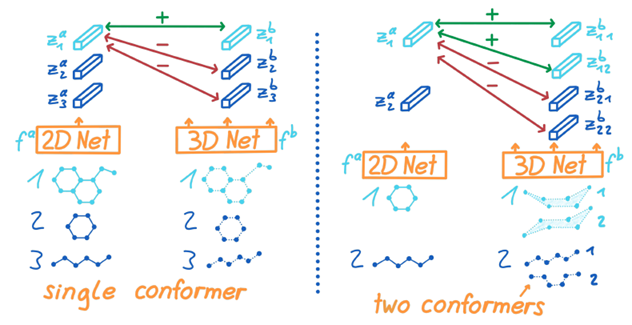
对比学习的损失函数为: \[ \mathcal{L}^{multi3D}=-\frac{1}{N}\sum\limits_{i=1}^{N}\left[\log\frac{\sum_{j=1}^{c}e^{sim(z_i^a,z_{i,j}^b)/\tau}}{\sum_{k=1,k\neq i}^{N}\sum_{j=1}^{c}e^{sim(z_i^a,z_{k,j}^b)/\tau}}\right] \]
实验结果
作者分别在QM9这个3D的下游任务上面以及一些2D的下游任务上面对模型的效果进行了测试。下面的表格中,蓝色代表相比于模型随机初始化之后训练的结果有提升,橙色代表结果下降。
下表为QM9数据集上的结果:
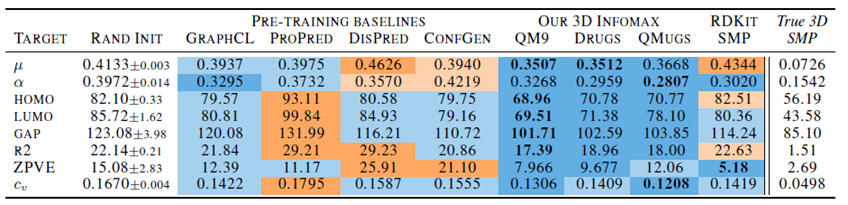
从中可以看出,作者提出的3D infomax相比于其它的几种预训练baseline在QM9数据集上的表现更好一些。表中的最右侧一列为使用3D GNN的预测结果,与之对比可以看出,在某些预测目标上,3D GNN的误差比2D GNN要小一个数量级,这也说明2D与3D的对比学习能够对2D GNN在3D任务上的预测起到一些作用,但是作用有限。
此外,作者也做了一些2D的下游任务:
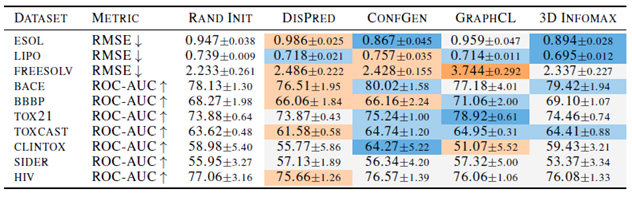
从中可以看出,由于对比学习之后2D GNN的编码中包含3D信息,因此在2D的下游任务上表现略有提升。
GraphMVP
概述
GraphMVP这一工作中,作者也使用了2D和3D结构做对比学习的思想。除此之外,还包含用2D编码生成3D编码以及用3D编码生成2D编码这一生成任务。总体设计如下图:
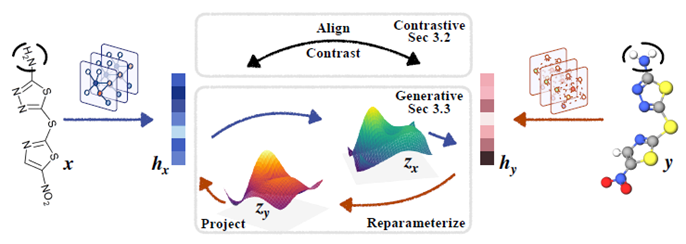
其中,2D的GNN为GIN,3D的GNN为SchNet。通过对比学习,能够学到数据之间的知识,而编码的互相生成则能够学习到分子2D与3D结构内部的知识。
与3D infomax类似,在预训练完成之后,就可以只使用2D GNN来做下游任务。
预训练设计
对比学习
与3D infomax类似,同一个分子的2D和3D编码组成的pair被认为是正类,不同分子的2D和3D编码组成pair被认为是负类。作者在对比学习任务中使用了两种不同的损失函数,在模型训练的时候把它看作超参数来调整: \[ \mathcal{L}_{\mathrm{infoNCE}}=-\frac{1}{2}\mathbb{E}_{p(\boldsymbol{x},\boldsymbol{y})} \left[\log\frac{\exp(f_\boldsymbol{x}(\boldsymbol{x},\boldsymbol{y}))}{\exp(f_\boldsymbol{x}(\boldsymbol{x},\boldsymbol{y}))+\sum_j\exp(f_\boldsymbol{x}(\boldsymbol{x}^j,\boldsymbol{y}))}+\log\frac{\exp(f_\boldsymbol{y}(\boldsymbol{y},\boldsymbol{x}))}{\exp(f_\boldsymbol{y}(\boldsymbol{y},\boldsymbol{x}))+\sum_j\exp(f_\boldsymbol{y}(\boldsymbol{y}^j,\boldsymbol{x}))}\right] \]
\[ \begin{aligned} \mathcal{L}_{\text{EBM-NCE}}=-\frac{1}{2}\mathbb{E}_{p(\boldsymbol{y})}\left[\mathbb{E}_{p_n(\boldsymbol{x}|\boldsymbol{y})}\log\left(1-\sigma(f_n(\boldsymbol{x},\boldsymbol{y}))\right)+\mathbb{E}_{p(\boldsymbol{x}|\boldsymbol{y})}\log\sigma(f_n(\boldsymbol{x},\boldsymbol{y}))\right]\\ -\frac{1}{2}\mathbb{E}_{p(\boldsymbol{x})}\left[\mathbb{E}_{p_n(\boldsymbol{y}|\boldsymbol{x})}\log\left(1-\sigma(f_\boldsymbol{y}(\boldsymbol{y},\boldsymbol{x}))\right)+\mathbb{E}_{p(\boldsymbol{y},\boldsymbol{x})}\log\sigma(f_\boldsymbol{y}(\boldsymbol{y},\boldsymbol{x}))\right] \end{aligned} \]
生成任务
由于不同的3D构象可能对应于同样的2D结构,加上3D的解码器通常比较复杂,因此作者在设计生成任务的时候,并不是让模型直接去生成2D结构或者3D构象,而是用了一个代理任务。这个代理任务类似于变分自编码器,给定一个分子结构的2D编码,首先将其映射到一个隐空间,然后再从隐空间中采样并以此生成对应的3D编码。用3D编码生成2D编码的过程也与之类似。
设\(\boldsymbol{x},\boldsymbol{y}\)分别为2D和3D的编码,这一生成任务的步骤以及损失函数如下: \[ {\boldsymbol{z_x}}={\boldsymbol{\mu_x}}+{\boldsymbol{\sigma_x}}\odot \boldsymbol{\epsilon} \\ {\boldsymbol{z_y}}={\boldsymbol{\mu_y}}+{\boldsymbol{\sigma_y}}\odot \boldsymbol{\epsilon} \\ \boldsymbol{\mu_{x}}=MLP\left(\boldsymbol{h_{x}}\right),\boldsymbol{\mu_{y}}=MLP\left(\boldsymbol{h_{y}}\right)\\ \boldsymbol{\sigma_{x}}=MLP\left(\boldsymbol{h_{x}}\right),\boldsymbol{\sigma_{y}}=MLP\left(\boldsymbol{h_{y}}\right)\\ \boldsymbol{\epsilon}\sim N(0,I) \]
\[ \begin{aligned} \mathcal{L}_G=\mathcal{L}_{\text{VRR}}=&\dfrac{1}{2}\left[\mathbb{E}_{q(\boldsymbol{z_x}|\boldsymbol{x})}\left[\|\boldsymbol{q_x}(\boldsymbol{z_x})-\text{SG}(\boldsymbol{h_y})\|^2\right]+\mathbb{E}_{q(\boldsymbol{z_y}|\boldsymbol{y})}\left[\|\boldsymbol{q_y}(\boldsymbol{z_y})-\text{SG}(\boldsymbol{h_x})\|_2^2\right]\right]\\ &+\dfrac{\beta}{2}\cdot\left[KL(q(\boldsymbol{z_x}|\boldsymbol{x})|\|p(\boldsymbol{z_x}))+KL(q(\boldsymbol{z_y}|\boldsymbol{y})|\|p(\boldsymbol{z_y}))\right] \end{aligned} \]
其中,SG代表Stop-Gradient,即阻止梯度反传。
损失函数
将对比学习任务与生成任务的损失函数加在一起,就得到了整体的损失函数: \[ \mathcal L_{\text{GraphMVP}}=\alpha_1\cdot\mathcal L_\text{C}+\alpha_2\cdot\mathcal L_\text{G} \] 其中,下标\(C\)和\(G\)分别代表对比学习任务和生成任务。
此外,它还可以和其它的生成任务或者对比学习任务结合,对应的损失函数为: \[ \mathcal{L}_{\mathrm{GraphMVP-G}}=\mathcal{L}_{\mathrm{GraphMVP}}+\alpha_{3}\cdot\mathcal{L}_{\mathrm{Generative~2D-SSL}} \\ \mathcal{L}_{\mathrm{GraphMVP-C}}=\mathcal{L}_{\mathrm{GraphMVP}}+\alpha_3\cdot\mathcal{L}_{\mathrm{Contrastive~2D-SSL}} \]
实验结果
作者在一些2D分子的下游数据集上进行实验,其结果如下表:
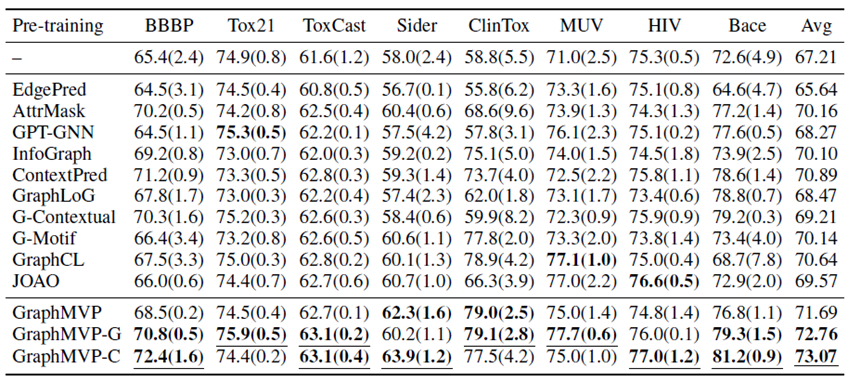
其中,\(G\)代表除了GraphMVP本身又额外加入了Attribute masking这一额外任务,而\(C\)代表额外加入Context prediction这一额外任务(这两任务的详细描述可参照本文的Pretrain-GNN相关内容)。
在平均意义上,GraphMVP相比于表中其它几种预训练方法的效果都要好,而且两个加入了额外任务的变体有着更好的效果。这说明一个分子的3D信息能够为2D的特征表示提供补充信息。
此外作者也做了一些消融实验,验证GraphMVP的预训练设计中真正起作用的地方:
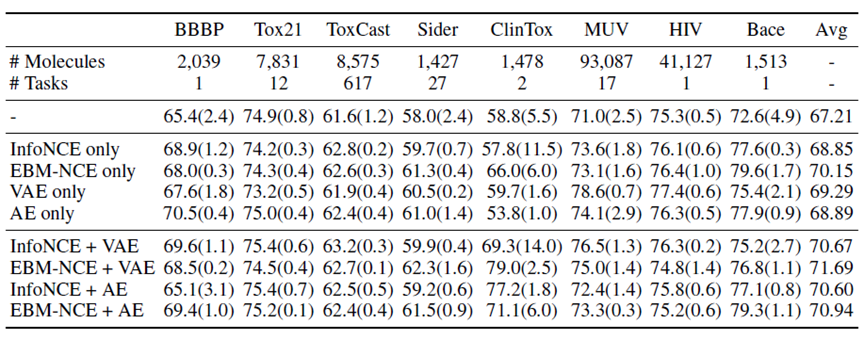
从这些结果中可以总结出三个结论:
- 单一的对比学习任务与生成任务都对下游任务有正向提升
- 对比任务与生成任务结合,能够取得更好的效果
- 生成任务中引入随机性(即使用VAE而不是AE)对学习到的特征表示有重要作用
基于去噪的方法
3D-EMGP
概述
3D-EMGP这一工作使用给原子加入随机噪声扰动,然后训练一个去噪的预训练模型,与此同时预测加入噪声的尺度。训练完成之后,便可以基于预训练的模型参数来做下游任务。整体框架如下图所示:
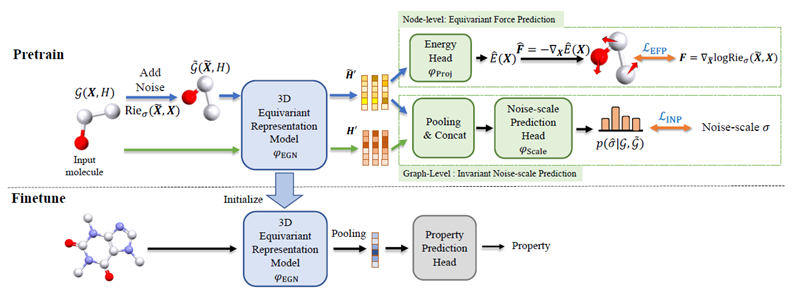
去噪任务设计
物理背景
分子的去噪预训练主要是基于这样的物理背景:一个分子处于平衡(或者称亚稳态)位置时,通常具有较低的能量,反映在分子的势能函数(即原子位置与分子能量之间的关系)上对应于局部最小值。势能函数是一个保守场,它只与原子位置有关,反映在数学上就是旋度为0。
如果对平衡态的原子位置加入一定的噪声干扰,则原子会偏离平衡位置,处于一个能量较高的非平衡状态。对于非平衡状态的分子,每个原子都有自发向平衡位置移动的趋势,即原子力,它与分子势能的关系可以表示为: \[ \boldsymbol{F}=-\nabla_{\boldsymbol{X}} E_p(\boldsymbol{X}) \] 此外,在统计物理中,有如下的玻尔兹曼分布率: \[ p_i=\frac{1}{Z}\exp\left(-\frac{E(\boldsymbol{X})}{kT}\right) \] 其中\(E\)代表体系的能量,\(k\)代表玻尔兹曼常数,\(T\)代表温度,\(Z\)为归一化常数。对上式做变换可得: \[ \nabla_{\boldsymbol{X}}\log p(\boldsymbol{X})\propto -\nabla_{\boldsymbol{X}}E(\boldsymbol{X}) =\boldsymbol{F} \] 这一表达式则又与score-based model很接近。得分匹配模型的损失函数为 \[ E_{p_{\text{data}}(\boldsymbol x)}\left[ ||\boldsymbol s_{\boldsymbol \theta}(\boldsymbol x)-\nabla_{\boldsymbol x}\log p_{\text{data}}(\boldsymbol x)||_2^2 \right] \] 这里的\(\boldsymbol s_{\boldsymbol \theta} (\boldsymbol x)=\nabla_{\boldsymbol x}\log p_\theta(\boldsymbol x)\),而根据玻尔兹曼分布律又有\(\nabla_{\boldsymbol{X}}\log p(\boldsymbol{X})\propto -\nabla_{\boldsymbol{X}}E(\boldsymbol{X}) =\boldsymbol{F}\),由此便可以将二者关联起来。也就是说,可以使用score model的训练方法来等价地训练一个预测原子力的模型。而score model目前常用的训练方法是去噪得分匹配,因此也同样可以设计去噪任务来训练模型。
基于原子力的去噪
由于分子的能量具有不变性,也就是无论分子如何旋转或平移,它所对应的能量都不改变。此外,原子力也应该具有旋转的等变性。因此编码器使用的是EGNN模型,它可以生成具有\(E(3)\)不变性的特征表示\(H'\): \[ H'=\varphi_\text{EGN}\left(\mathbf{X},H\right)\\ \] 之后,基于去噪的物理背景,设计去噪头(energy head)如下: \[ \begin{aligned} &E(\mathbf{X})=\varphi_\text{Proj}\left(\sum\limits_{i=1}^{N}\boldsymbol{h}_{i}'\right)\\ &F(\mathbf{X})=-\lim\limits_{\Delta X\to 0}\dfrac{\Delta E}{\Delta\mathbf{X}}=-\nabla_\mathbf{X}E(\mathbf{X}) \end{aligned} \] 但是原始的score-based model中所使用的正态分布及其对应的训练目标,放在分子去噪任务上面并不合适,因为正态分布并不具有不变性。因此,作者使用了黎曼-高斯分布来代替普通的正态分布,即: \[ p_{\sigma}(\tilde{\boldsymbol{X}}\mid \boldsymbol{X})=\operatorname{Rie}_{\sigma}(\tilde{\boldsymbol{X}}\mid \boldsymbol{X}):=\dfrac{1}{Z(\sigma)}\exp\left(-\dfrac{d^2(\tilde{\boldsymbol{X}},\boldsymbol{X})}{4\sigma^2}\right) \] 其中\(Z\)为配分函数,\(d(X_{1},\boldsymbol{X}_{2})=\|\boldsymbol{Y}_{1}^{\top}\boldsymbol{Y}_{1}-\boldsymbol{Y}_{2}^{\top}\boldsymbol{Y}_{2}\|_{F}\),\(\boldsymbol{Y}=\boldsymbol{X}-\mu(\boldsymbol{X})\)代表整体平移使得质心为0之后的坐标。
从中计算可得,去噪的预测目标为: \[ \nabla_{\tilde{\boldsymbol{X}}}\log p_{\sigma}(\tilde{\boldsymbol{X}}|\boldsymbol{X})=-\dfrac{1}{\sigma^2}\big[(\tilde{\boldsymbol{Y}}\tilde{\boldsymbol{Y}}^{\top})\tilde{\boldsymbol{Y}}-(\tilde{\boldsymbol{Y}}\boldsymbol{Y}^{\top})\boldsymbol{Y}\big] \] 作者也证明了这样的黎曼-高斯分布可以满足双\(E(3)\)不变性(即条件概率中的输入和条件同时具有不变性)。
由于配分函数的存在,无法直接通过函数变换的方式从黎曼-高斯分布中采样,需要借助如下的朗之万动力学采样:

预测噪声尺度
除了去噪任务之外,作者还设计了预测噪声尺度任务。具体做法是将带有噪声与不带噪声的两个分子构象分别送入编码器中,得到二者的特征向量。然后通过池化操作生成两个全局的特征向量。之后,将二者拼接起来,并送入一个预测头中,预测不同噪声尺度的概率: \[ p\in\mathbb{R}^{L}=\varphi_{\mathbf{Scale}}\left(\boldsymbol{u}\|\tilde{\boldsymbol{u}}\right) \]
损失函数
模型的损失函数由两部分组成: \[ \mathcal{L}=\lambda_1\mathcal{L}_\mathrm{EFP-Final}+\lambda_2\mathcal{L}_\mathrm{INP} \] 其中,EFP指的是预测噪声的任务,它的损失函数即去噪误差,具体为: \[ \mathcal{L}_{\mathrm{EFP-Final}}=\mathbb{E}_{\mathcal{G}\sim G,l\sim U(1,L),\tilde{\boldsymbol{X}}\sim p_{\sigma_{l}}(\tilde{\boldsymbol{X}},\boldsymbol{\boldsymbol{X}})}\big[\|\boldsymbol{F}(\tilde{\boldsymbol{X}})-\frac{1}{\alpha}\nabla_{\tilde{X}}\log p_{\sigma_{l}}(\tilde{\boldsymbol{X}}|\boldsymbol{X})\|_{F}^{2}\big] \] INP指的是预测噪声尺度,损失函数为: \[ \mathcal{L}_{\mathrm{INP}}=\mathbb{E}_{\mathcal{G}\sim\mathbb{G},l\sim U(1,L),\tilde{\mathbf{X}}\sim p_{\sigma_l}(\tilde{\mathbf{X}}|\mathbf{X})}\big[\mathcal{L}_{\mathrm{CE}}\left(\mathbb{I}[l],p\right)\big] \] CE代表交叉熵损失,\(\mathbb{I}[l]\)代表噪声尺度的one-hot编码。
实验结果
预训练效果
作者分别在MD17和QM9这两个数据集上做了实验。下面是MD17数据集上的结果:
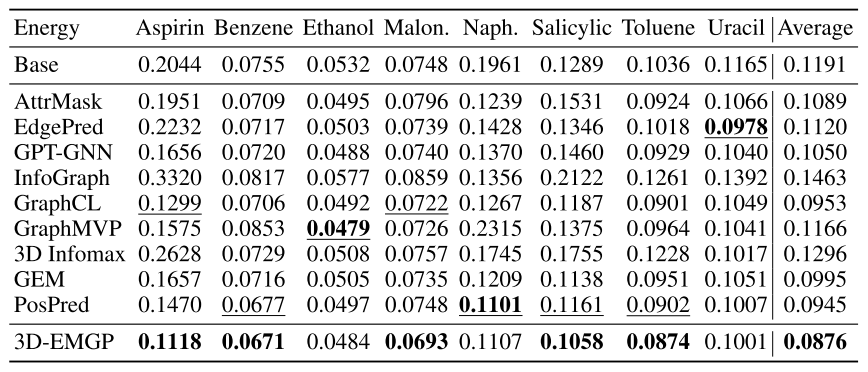
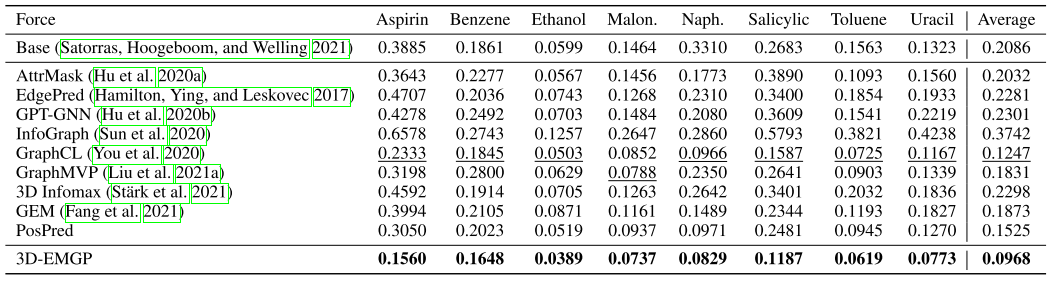
从中可以看出,去噪预训练对于能量的预测提升效果不是很明显,但是对于力的预测有着很明显的提升效果。这也说明去噪预训练与原子力的预测有着很强的关联性。
在QM9数据集上的结果如下表:
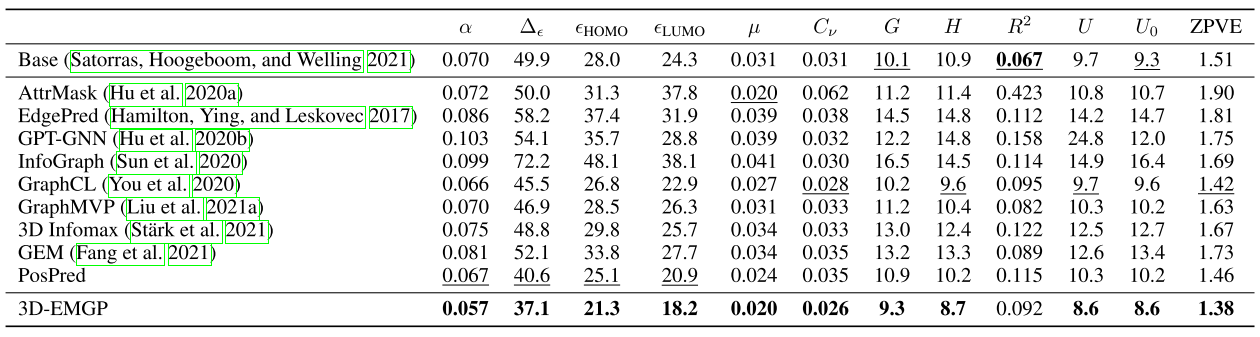
在大多数任务上,去噪预训练方法对模型的提升效果都很明显。
此外,相比于表中其它的几种预训练方法,去噪预训练的提升也更大一些。表中的其它预训练方法在下游任务上都只有微弱提升甚至是下降,而去噪预训练在下游任务上基本都能起到提升的效果。
消融实验
下表为作者在MD17数据集上所做的消融实验:
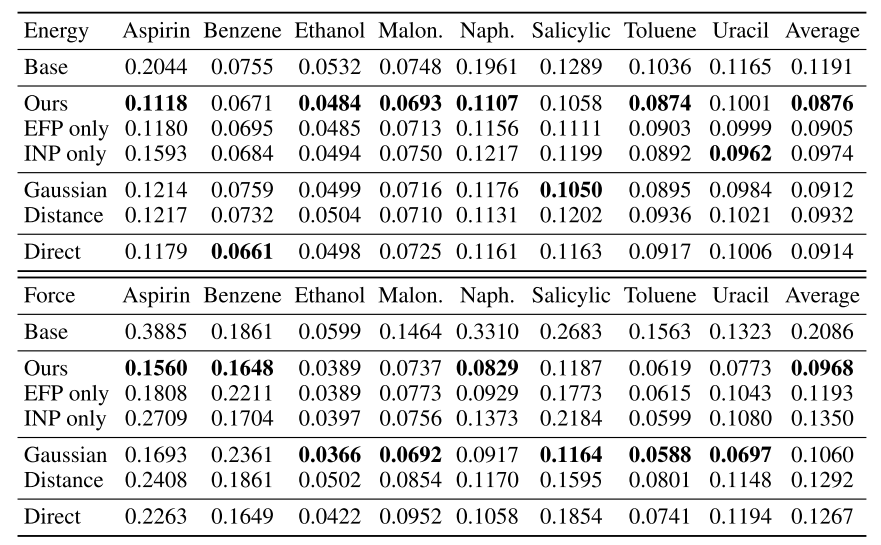
其中,EFP only代表只做去噪,INP only代表只做噪声尺度的预测,Gaussian代表加入高斯噪声,distance代表在两原子之间的距离上加噪,direct代表去噪头直接预测噪声。
从中可以得到下面的结论:
- 去噪与预测噪声尺度这两个预训练任务对于下游任务都有帮助,但是去噪任务的帮助更大
- 如果将加入的噪声换成高斯噪声,或者是直接在原子距离上加噪,则去噪预训练的效果会变差。这说明考虑噪声概率分布的不变性是有必要的
- 如果让去噪头直接预测噪声,则预训练效果也会变差。这可能跟分子力属于保守力有关,如果直接预测噪声则很可能无法保证这一特性
此外作者也用不同的backbone做了实验:
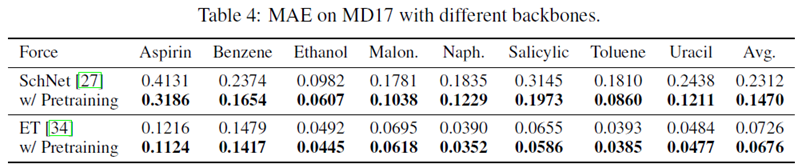
结果说明,这一去噪预训练的方法在换用两种不同的模型之后仍有效。
数据集质量的影响
作者也验证了,如果使用带有噪声的低质量预训练数据集,这种去噪预训练的方法是否有效。在GEOM-QM9数据集上为每个原子的位置加入一个正态分布的随机噪声\(\boldsymbol{X}^{\prime}=\boldsymbol{X}+ 0.1\boldsymbol{\epsilon},\boldsymbol{\epsilon}\sim \mathcal{N}(0,\boldsymbol{I}^{N\times3})\),然后用这样的带噪数据集做预训练,在QM9和MD17这两个下游任务上面的表现如下表:
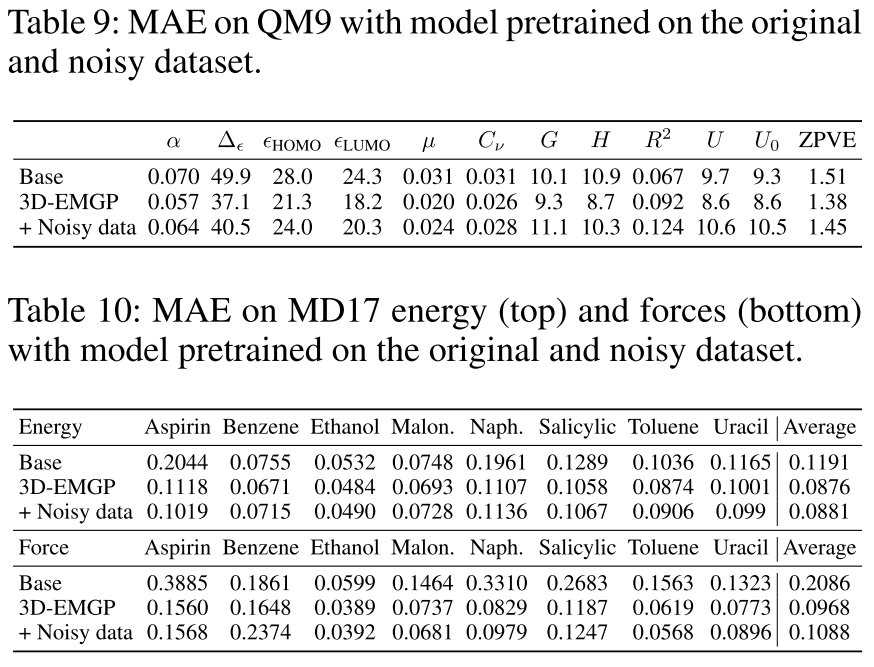
从中可以看到,稍低质量的带噪数据集仍然可以做预训练,但是相比于干净数据集的效果会有所下降。由此想到的另一个延申问题就是,当预训练数据集的噪声进一步增大到什么程度时,这样的预训练就没有效果或者起反作用?
结果可视化
作者也以MD17数据集为例,对训练结果做了可视化。具体做法是,对于不同预训练方法得到的预训练模型,固定它们的backbone,然后用MD17的aspirin分子数据集对energy head进行微调训练。有些预训练方法并没有energy head,对于这些方法则是在这些模型后面加入一个MLP作为energy head。
训练完成之后,在数据集中随机选取一个构象,并基于高斯分布随机采样两个方向矩阵\(\boldsymbol D_1,\boldsymbol D_2\in \mathbb{R}^{N\times 3}\),以此对原子坐标进行扰动: \[ \{\tilde{\boldsymbol X}(i,j)|\tilde{\boldsymbol X}(i,j)=\boldsymbol X+i \boldsymbol D_1+j \boldsymbol D_2\} \] 用energy head的预测结果,便可以得到如下的能量面可视化示意图:
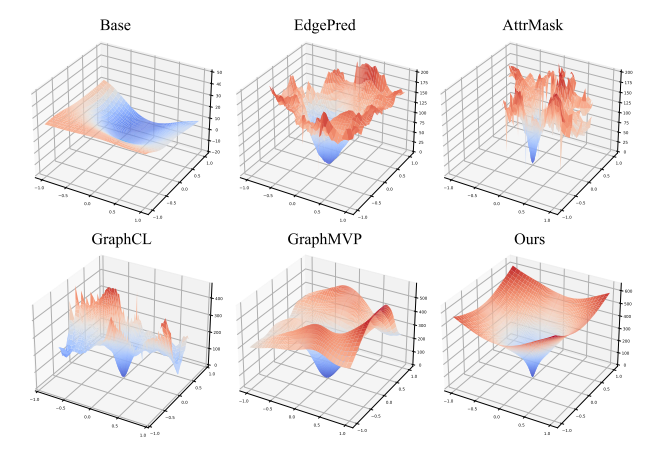
从中可以看出,作者提出的预训练方法在原始的原子构象处是一个局部最小值,然后随着坐标扰动的增大,对应的能量也越来越大,这也符合物理规律。而其它几种预训练方法则会生成高低起伏的能量面。此外,对于base模型,可能是因为数据过少导致它无法学习到数据中所包含的物理规律。
一个近似工作
另一个与之思想比较类似的工作是Pre-training via Denoising for Molecular Property Prediction,但是略有些不同之处。下面简单介绍一些它们的区别。
首先是在3D-EMGP中,设计了几种不同的噪声尺度(即\(\sigma\))。而这一工作中作者所使用的噪声尺度为一个固定值,在训练的时候将其作为一个超参数来调整。从统计物理的角度来看,这里的\(\sigma\)其实起到了玻尔兹曼分布律中温度\(T\)的角色,因此可以近似认为如果使用多种噪声尺度,就相当于是让模型学会在不同的温度下做去噪。
此外就是作者只是简单地加入了正态分布的噪声,没有像3D-EMGP那样考虑噪声与原子能量之间的关联性。GNN模型也是直接去预测噪声。因此去噪训练的损失函数也有更简单的形式: \[ \mathbb{E}_{q_{\sigma}(\tilde{\mathbf{x}},\mathbf{x})}\left[\left\|\mathrm{GNN}_{\theta}(\tilde{\mathbf{x}})-\nabla_{\tilde{\mathbf{x}}}\log{q_{\sigma}}(\tilde{\mathbf{x}}\mid\mathbf{x})\right\|^{2}\right]=\mathbb{E}_{q_{\sigma}(\tilde{\mathbf{x}},\mathbf{x})}\left[\left\|\mathrm{GNN}_{\theta}(\tilde{\mathbf{x}})-\dfrac{\mathbf{x}-\tilde{\mathbf{x}}}{\sigma^{2}}\right\|^{2}\right] \] 从物理上来说,这样的训练目标会带来一些问题。考虑比较极端的情况,比如加入的噪声刚好使得整个分子体系做平移,或者是噪声刚好是使得整个体系做旋转,此时从物理规律上来说噪声应当为0。因此个人认为这种办法应该还是存在一些改进空间的。或者是能够从概率分布的角度证明这种情况对于损失函数的影响可以忽略不计,即极端情况出现的概率很小甚至为0。
除了做去噪预训练,作者在做下游任务的时候还使用了Noisy Nodes作为辅助损失函数。Noisy Nodes这一工作其实与去噪预训练的方法很相似,但它是将结点去噪作为模型在下游任务上进行训练时的一个辅助任务,用于对结点特征做正则化,防止其出现过平滑的现象。
下图说明了去噪预训练和noisy nodes在下游任务上分别起到的效果:
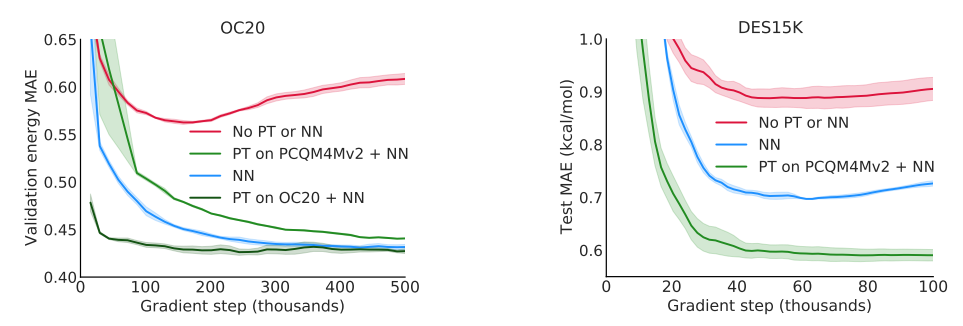
从中可以看出,在加入noisy nodes这个辅助任务之后,相比于base模型的误差会有所降低,而在加入了去噪预训练之后则又会进一步降低,这说明它们对于下游任务都有所帮助,而且可以同时使用。
SE(3)-DDM
概述
SE(3)-DDM这一工作同样是使用去噪做预训练,但是它是从对比学习的角度设计预训练的损失函数。此外,它在加噪声的时候是在两原子对的位置矢量上进行操作的,而去噪也是在原子对之间的位置矢量进行。下面将详细介绍它的模型设计以及结果。
任务设计
互信息最大化
作者所设计的互信息最大化目标函数是基于如下的物理假设:对于一个数据集中所包含的所谓亚稳态分子构象,它并不是真正地位于亚稳态位置。由于无法避免地系统误差、计算误差等的存在,以及温度引起的热振动的影响,最终导致它实际上处于略微偏离亚稳态的地方。
因此,作者设计了下图所示的对比学习任务:
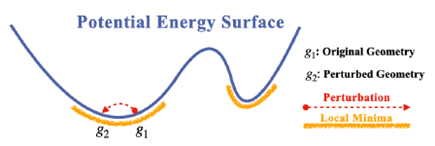
在原始位置\(g_1\)的基础上,加入少量噪声得到\(g_2\),然后做两分子构象之间的互信息最大化: \[ I(G_1;G_2)=\mathbb{E}_{p(g_1,g_2)}\Big[\log\dfrac{p(g_1,g_2)}{p(g_1)p(g_2)}\Big]\geq\dfrac{1}{2}\mathbb{E}_{p(g_1,g_2)}\Big[\log p(g_1|g_2)+\log p(g_2|g_1)\Big]\triangleq\mathcal{L}_{\text{MI}} \] 将其中的概率密度用能量函数来定义,上式可以变为: \[ \begin{aligned} \mathcal{L}_{MI}&=\frac{1}{2}\mathbb{E}_{p(g_{1},g_{2})}\Big[\log p(g_{1}|g_{2})\Big]+\frac{1}{2}\mathbb{E}_{p(g_{1},g_{2})}\Big[\log p(g_{2}|g_{1})\Big]\\ &=\frac{1}{2}\mathbb{E}_{p(g_{1},g_{2})}\Big[\log p((\boldsymbol{X}_{1},\boldsymbol{R}_{1})|(\boldsymbol{X}_{2},\boldsymbol{R}_{2}))\Big]+\frac{1}{2}\mathbb{E}_{q(g_{1},g_{2})}\Big[\log p((\boldsymbol{X}_{2},\boldsymbol{R}_{2})|(\boldsymbol{X}_{1},\boldsymbol{R}_{1}))\Big]\\ &=\frac{1}{2}\mathbb{E}_{p(g_{1},g_{2})}\Big[\log p(\boldsymbol{R}_{1}|g_{2})\Big]+\frac{1}{2}\mathbb{E}_{q(g_{1},g_{2})}\Big[\log p(\boldsymbol{R}_{2}|g_{1})\Big]\\ &=\frac{1}{2}\mathbb{E}_{p(g_{1},g_{2})}\left[\log\frac{\exp (f(\boldsymbol{R}_{1},g_{2}))}{A_{\boldsymbol{R}_1|g_2}}\right]+\frac{1}{2}\mathbb{E}_{p(g_{1},g_{2})}\left[\log\frac{\exp (f(\boldsymbol{R}_{2},g_{1}))}{A_{\boldsymbol{R}_2|g_1}}\right] \end{aligned} \]
引入得分函数
由于上式中包含配分函数难以求解,因此考虑使用score-based model,即定义 \[ s(\boldsymbol{R}_1,g_2)\triangleq\nabla_{\boldsymbol{R}_1}\log p(\boldsymbol{R}_1|g_2)=\nabla_{\boldsymbol{R}_1}f(\boldsymbol{R}_1,g_2) \] 之后,便可以用得分函数去近似能量函数的梯度,以训练得分函数作为代理任务。作者设计的得分函数可以表示为: \[ s(\boldsymbol{R}_{1},g_{2})_{i}=\sum_{j\neq i}\frac{\partial f(\boldsymbol{R}_{1},g_{2})}{\partial d_{1,i j}}\cdot\frac{\partial d_{1,i j}}{\partial \boldsymbol{r}_{1,i}}=\sum_{j\neq i}\frac{1}{d_{1,i j}}\cdot s(d_{1},g_{2})_{i j}\cdot(\boldsymbol{r}_{1,i}-\boldsymbol{r}_{1,j}) \] 其中,\(s(d_1,g_2)_{ij}\)的设计如下: \[ h(g_2)_i=\text{3D-GNN}(T(g_2)) \\ h(g_2)_{ij}=h(g_2)_i+h(g_2)_j \\ s_\theta(\tilde{d}_1,g_2)_{ij}=\operatorname{MLP}\big(\operatorname{MLP}(\tilde{d}_{1,i j})\oplus h(g_2)_{ij}\big) \] 其中的3D-GNN用的是PaiNN结构。
使用去噪得分匹配的方法做训练,则最终的训练目标为: \[ \begin{aligned} \mathcal{L}_{\text{SE(3)-DDM}}&=\frac{1}{2L}\sum_{l=1}^{L}\sigma_{l}^{\beta}\mathbb{E}_{p_{\text{data}(d_{1}|g_{2})}}\mathbb{E}_{q(\tilde{d}_{1}|d_{1},g_{2})}\left[\left\|\frac{s_{\boldsymbol{\theta}}(\tilde{d}_{1},g_{2})}{\sigma_{l}}-\frac{d_{1}-\tilde{d}_{1}}{\sigma_{l}^{2}}\right\|_{2}^{2}\right]\\ &=\frac{1}{2L}\sum_{l=1}^{L}\sigma_{l}^{\beta}\mathbb{E}_{p_{\text{data}(d_{2}|g_{1})}}\mathbb{E}_{q(\tilde{d}_{2}|d_{2},g_{1})}\left[\left\|\frac{s_{\boldsymbol{\theta}}(\tilde{d}_{2},g_{1})}{\sigma_{l}}-\frac{d_{2}-\tilde{d}_{2}}{\sigma_{l}^{2}}\right\|_{2}^{2}\right]\\ \end{aligned} \] 但是进一步思考,这样的加噪方式是否会引起如下图所示的问题?
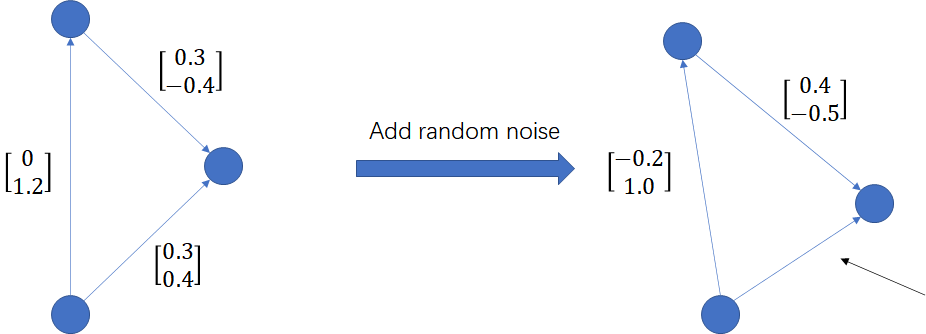
其中,箭头所指的向量应该为\([0.2,0.5]\)才能满足向量的封闭性要求。但是如果直接加入随机噪声,不考虑向量的封闭性约束,从概率上讲几乎不可能生成满足这样的要求。这样的加噪方式是否会对预训练造成影响不得而知。
训练步骤
模型的训练步骤可以总结为如下的算法流程:

其中,第四步加噪声的时候会加入很小的噪声,也就是用\(\sigma\)只有零点几的正态分布生成噪声。
实验结果
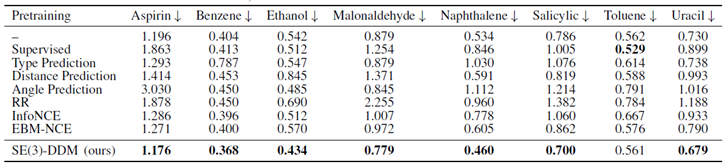
作者分别在QM9、MD17这两个分子性质预测任务,以及蛋白质结合的任务上分别做了实验。下表是QM9和MD17数据集的结果:
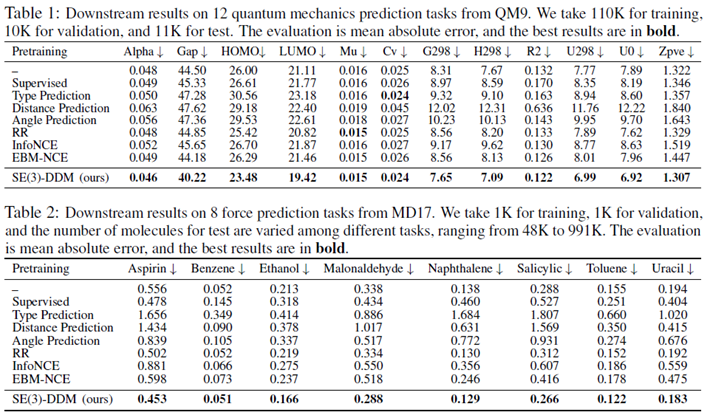
表中的Supervised指的是用预训练数据集中的能量来做监督学习预训练,RR指的是类似于GraphMVP这一工作中的生成式预训练方法,Info-NCE和EBM-NCE指的是用对比学习的方法做预训练。从中可以看出,除了去噪预训练,其它几种预训练方法在下游任务上起到的作用很小,甚至起到了反作用。
而在蛋白质结合预测任务上,也有类似的结论:
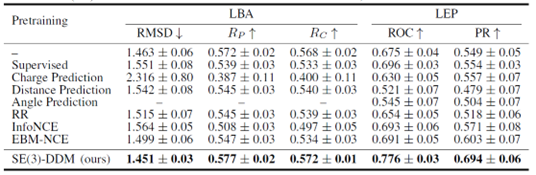
此外,为了排除Backbone的影响,作者也用SchNet作为Backbone做了消融实验,证明了这种去噪预训练的方法仍然有效: