简介
卡尔曼滤波是一种根据线性系统状态方程,通过使用系统的输入输出与观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰影响,所以最优估计也可以看做是滤波过程。简单地说,卡尔曼滤波要解决的是如何从多个满足高斯分布的不确定性信号中提取相对精确的信号。
举一个简单的例子,考虑平面轨道上面的一个小车,我们要估计它在每个时间步的位置。现在有一个模型,可以通过\(t\)时刻的位置来计算出\(t+1\)时刻的位置,但是模型的计算结果仅仅是理论值,实际会受到各种因素的影响;同时有一个传感器,可以用于测量小车在\(t+1\)时刻的位置,但是传感器也存在一定的误差。使用卡尔曼滤波,就可以把\(t+1\)时刻模型的计算值与传感器的测量值按照一定的权重进行合并,得到一个新的估计值,而这个值又可以用于\(t+2\)时刻的迭代过程。这一过程可以表示为下图:
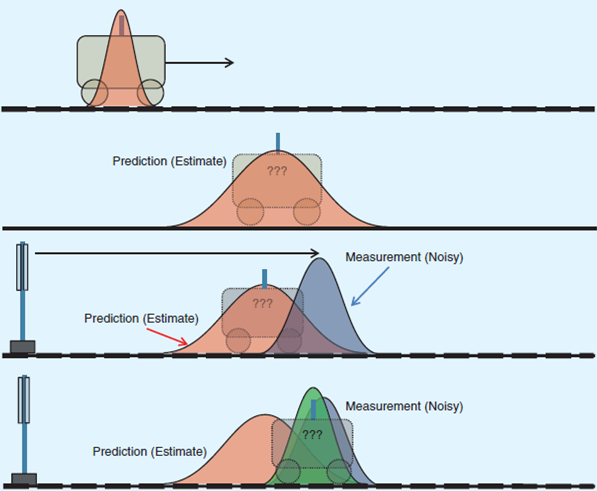
基本原理
假设系统在\(t\)时刻的状态可以由之前\(t-1\)时刻的状态按照如下公式迭代而得: \[ \boldsymbol{x}_t=\boldsymbol{F}_t\boldsymbol{x}_{t-1}+\boldsymbol{B}_t\boldsymbol{u}_t+\boldsymbol{w}_t \] 其中,
- \(\boldsymbol{x}_t\)代表时刻\(t\)的状态向量,其中包含了系统的状态。以小车的例子,系统的状态可以是小车的位置、速度、加速度、朝向等信息。
- \(\boldsymbol{u}_t\)代表时刻\(t\)的控制向量。以小车的例子,控制向量可以包含转向角、进气量的设置、刹车力度等。
- \(\boldsymbol{F}_t\)代表时刻\(t\)的状态转移矩阵,通过它可以计算\(t-1\)时刻的状态对于\(t\)时刻状态的影响。以小车的例子来说,\(t-1\)时刻的位置和速度会影响到\(t\)时刻的位置。
- \(\boldsymbol{B}_t\)代表时刻\(t\)的控制输入矩阵,通过它可以计算\(t\)时刻加入的控制向量对于状态的影响。以小车的例子,就是计算进气量的设置对于小车位置和速度等状态的影响。
- \(\boldsymbol{w}_t\)代表状态向量中的噪声项,通常假设它服从一个均值为0,协方差矩阵为\(\boldsymbol{Q}_t\)的多元正态分布。
此外,系统的某些测量值也可以通过如下模型计算: \[ \boldsymbol{z}_t=\boldsymbol{H}_t\boldsymbol{x}_t+\boldsymbol{v}_t \] 其中,
- \(\boldsymbol{z}_t\)是测量值组成的向量。
- \(\boldsymbol{H}_t\)代表转移矩阵,它将系统的状态映射为对应的测量值。
- \(\boldsymbol{v}_t\)代表测量值的噪声项,同样假设它服从一个均值为0,协方差矩阵为\(\boldsymbol{R}_t\)的多元正态分布。
卡尔曼滤波基于上述两个公式,通过对先验知识、系统模型的预测值以及带有噪音的测量值进行融合,从而估计出\(t\)时刻的状态向量\(\hat{\boldsymbol{x}}_t\)。卡尔曼滤波算法包括两个阶段,第一阶段是预测,第二阶段是使用测量值进行更新。在下文中,下标\(t|t-1\)代表预测阶段的先验估计值,下标\(t|t\)代表使用测量值更新之后的后验估计。
在预测阶段,主要是通过状态转移方程来对\(t\)时刻的状态进行预测: \[ \begin{aligned} \hat{\boldsymbol{x}}_{t|t-1}=&\boldsymbol{F}_t\hat{\boldsymbol{x}}_{t-1|t-1}+\boldsymbol{B}_t\boldsymbol{u}_t \\ \boldsymbol{P}_{t|t-1}=&\boldsymbol{F}_t\boldsymbol{P}_{t-1|t-1}\boldsymbol{F}_t^T+\boldsymbol{Q}_t \end{aligned} \] 矩阵\(\boldsymbol{P}_t\)代表了\(t\)时刻状态向量估计值\(\hat{\boldsymbol{x}}_t\)的协方差矩阵(或者说估计误差的协方差矩阵,两种表达方式等价),它反映了估计值的可信程度。在\(t=0\)对应的初始态,将其直接设为单位矩阵即可,在后续的迭代过程中它会被自动调整。
在更新阶段,通过测量值对状态转移方程的值进行修正: \[ \begin{aligned} \hat{\boldsymbol{x}}_{t|t}=&\hat{\boldsymbol{x}}_{t|t-1}+\boldsymbol{K}_t(\boldsymbol{z}_t-\boldsymbol{H}_t\hat{\boldsymbol{x}}_{t|t-1}) \\ \boldsymbol{P}_{t|t}=&\boldsymbol{P}_{t|t-1}-\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{P}_{t|t-1} \end{aligned} \] 其中\(\boldsymbol{K}_t\)代表卡尔曼增益,它表征了状态最优估计值中模型预测误差和测量误差的比重。当\(\boldsymbol{K}_t=\boldsymbol{0}\)时,代表模型预测误差为0,系统的状态值完全取决于模型预测值;而当\(\boldsymbol{K}_t=\boldsymbol{1}\)时,则相当于测量误差为0,系统的状态值完全取决于测量值。卡尔曼增益也是卡尔曼滤波的核心,它的计算公式为: \[ \boldsymbol{K}_t=\boldsymbol{P}_{t|t-1}\boldsymbol{H}_t^T(\boldsymbol{H}_t\boldsymbol{P}_{t|t-1}\boldsymbol{H}_t^T+\boldsymbol{R}_t)^{-1} \]
下文将详细说明卡尔曼增益矩阵的推导过程。
推导
最小二乘法
我们假设系统在\(t\)时刻的真实状态为\(\boldsymbol{x}_t\),真实情况下噪声是无法避免的,因此只能使\(t\)时刻的后验状态预测值\(\hat{\boldsymbol{x}}_{t|t}\)尽可能的接近\(\boldsymbol{x}_t\)。假设误差\(\boldsymbol{e}_t=\boldsymbol{x}_t-\hat{\boldsymbol{x}}_{t|t}\)服从多元正态分布\(\boldsymbol{e}_t\sim N(\boldsymbol{0},\boldsymbol{P}_t)\),其中\(\boldsymbol{P}_t\)代表协方差矩阵。我们的目标是使得方差最小(其实就是最小二乘法),即协方差矩阵\(\boldsymbol{P}_t\)的迹(即对角线元素之和)最小。
\(\boldsymbol{P}_t\)的表达式可以写为: \[ \boldsymbol{P}_t=E[(\boldsymbol{x}_t-\hat{\boldsymbol{x}}_{t|t})(\boldsymbol{x}_t-\hat{\boldsymbol{x}}_{t|t})^T] \] 我们首先求误差\(\boldsymbol{x}_t-\hat{\boldsymbol{x}}_{t|t}\)的值。将\(\hat{\boldsymbol{x}}_{t|t}=\hat{\boldsymbol{x}}_{t|t-1}+\boldsymbol{K}_t(\boldsymbol{z}_t-\boldsymbol{H}_t\hat{\boldsymbol{x}}_{t|t-1})\)和\(\boldsymbol{z}_t=\boldsymbol{H}_t\boldsymbol{x}_t+\boldsymbol{v}_t\)代入,可得: \[ \begin{aligned} \boldsymbol{x}_t-\hat{\boldsymbol{x}}_{t|t}=& \boldsymbol{x}_t -\hat{\boldsymbol{x}}_{t|t-1}-\boldsymbol{K}_t(\boldsymbol{z}_t-\boldsymbol{H}_t\hat{\boldsymbol{x}}_{t|t-1}) \\ =& \boldsymbol{x}_t -\hat{\boldsymbol{x}}_{t|t-1}-\boldsymbol{K}_t\boldsymbol{z}_t+\boldsymbol{K}_t\boldsymbol{H}_t\hat{\boldsymbol{x}}_{t|t-1} \\ =& \boldsymbol{x}_t -\hat{\boldsymbol{x}}_{t|t-1}-\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{x}_t-\boldsymbol{K}_t\boldsymbol{v}_t+\boldsymbol{K}_t\boldsymbol{H}_t\hat{\boldsymbol{x}}_{t|t-1} \\ =& (\boldsymbol{x}_t -\hat{\boldsymbol{x}}_{t|t-1}) -\boldsymbol{K}_t\boldsymbol{H}_t(\boldsymbol{x}_t -\hat{\boldsymbol{x}}_{t|t-1})-\boldsymbol{K}_t\boldsymbol{v}_t \\ =& (\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)(\boldsymbol{x}_t -\hat{\boldsymbol{x}}_{t|t-1})-\boldsymbol{K}_t\boldsymbol{v}_t \end{aligned} \] 其中,\(\boldsymbol{x}_t -\hat{\boldsymbol{x}}_{t|t-1}\)也被称为先验误差,为了简便起见,我们将其记为\(\boldsymbol{e}_{t|t-1}=\boldsymbol{x}_t -\hat{\boldsymbol{x}}_{t|t-1}\)。则\(\boldsymbol{P}_t\)的表达式可以写为: \[ \begin{aligned} \boldsymbol{P}_t=&E[(\boldsymbol{x}_t-\hat{\boldsymbol{x}}_{t|t})(\boldsymbol{x}_t-\hat{\boldsymbol{x}}_{t|t})^T] \\ =& E[((\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)\boldsymbol{e}_{t|t-1}-\boldsymbol{K}_t\boldsymbol{v}_t)((\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)\boldsymbol{e}_{t|t-1}-\boldsymbol{K}_t\boldsymbol{v}_t)^T] \\ =& E[(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)\boldsymbol{e}_{t|t-1}\boldsymbol{e}_{t|t-1}^T(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T-(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)\boldsymbol{e}_{t|t-1}\boldsymbol{v}_t^T\boldsymbol{K}_t^T-\boldsymbol{K}_t\boldsymbol{v}_t\boldsymbol{e}_{t|t-1}^T(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T+\boldsymbol{K}_t\boldsymbol{v}_t\boldsymbol{v}_t^T\boldsymbol{K}_t^T]\\ =&E[(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)\boldsymbol{e}_{t|t-1}\boldsymbol{e}_{t|t-1}^T(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T]-E[(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)\boldsymbol{e}_{t|t-1}\boldsymbol{v}_t^T\boldsymbol{K}_t^T]-E[\boldsymbol{K}_t\boldsymbol{v}_t\boldsymbol{e}_{t|t-1}^T(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T]+E[\boldsymbol{K}_t\boldsymbol{v}_t\boldsymbol{v}_t^T\boldsymbol{K}_t^T] \end{aligned} \] 由于\(\boldsymbol{K}_t\),\(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t\)为常量,因此有: \[ E[(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)\boldsymbol{e}_{t|t-1}\boldsymbol{v}_t^T\boldsymbol{K}_t^T]=(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)E[\boldsymbol{e}_{t|t-1}\boldsymbol{v}_t^T]\boldsymbol{K}_t^T \\ E[\boldsymbol{K}_t\boldsymbol{v}_t\boldsymbol{e}_{t|t-1}^T(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T]=\boldsymbol{K}_t E[\boldsymbol{v}_t \boldsymbol{e}_{t|t-1}^T](\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T \] 测量误差\(\boldsymbol{v}_t\)与先验误差\(\boldsymbol{e}_{t|t-1}\)相互独立,因此: \[ E[\boldsymbol{e}_{t|t-1}\boldsymbol{v}_t^T]=0,~~E[\boldsymbol{v}_t \boldsymbol{e}_{t|t-1}^T]=0 \] 故\(\boldsymbol{P}_t\)的表达式可以进一步写为: \[ \begin{aligned} \boldsymbol{P}_t=&E[(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)\boldsymbol{e}_{t|t-1}\boldsymbol{e}_{t|t-1}^T(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T]+E[\boldsymbol{K}_t\boldsymbol{v}_t\boldsymbol{v}_t^T\boldsymbol{K}_t^T] \\ =&(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t) E[\boldsymbol{e}_{t|t-1}\boldsymbol{e}_{t|t-1}^T](\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T+\boldsymbol{K}_t E[\boldsymbol{v}_t\boldsymbol{v}_t^T]\boldsymbol{K}_t^T \end{aligned} \] 其中,\(E[\boldsymbol{e}_{t|t-1}\boldsymbol{e}_{t|t-1}^T]\)其实相当于是\(\boldsymbol{P}_{t|t-1}\),即先验估计值(或先验误差)的协方差矩阵,因此上式可以进一步化简为: \[ \begin{aligned} \boldsymbol{P}_t=&(\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t) \boldsymbol{P}_{t|t-1} (\boldsymbol{I}-\boldsymbol{K}_t\boldsymbol{H}_t)^T+\boldsymbol{K}_t \boldsymbol{R}_t\boldsymbol{K}_t^T \\ =&\boldsymbol{P}_{t|t-1} -\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{P}_{t|t-1}-\boldsymbol{P}_{t|t-1}\boldsymbol{H}_t^T\boldsymbol{K}_t^T+\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{P}_{t|t-1}\boldsymbol{H}_t^T\boldsymbol{K}_t^T+\boldsymbol{K}_t \boldsymbol{R}_t\boldsymbol{K}_t^T \end{aligned} \] 我们的目标是求矩阵\(\boldsymbol{K}_t\)的值,使得\(tr(\boldsymbol{P}_t)\)最小,这可以看作是对\(\boldsymbol{P}_t\)的各个部分分别求迹。此外由于转置操作不改变矩阵对角线的元素,可以对公式做进一步的化简。因此可得: \[ tr(\boldsymbol{P}_t)=tr(\boldsymbol{P}_{t|t-1}) -2tr(\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{P}_{t|t-1})+ tr(\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{P}_{t|t-1}\boldsymbol{H}_t^T\boldsymbol{K}_t^T)+tr(\boldsymbol{K}_t \boldsymbol{R}_t\boldsymbol{K}_t^T) \] 将上式对\(\boldsymbol{K}_t\)求偏导,可得: \[ \begin{aligned} \frac{\partial tr(\boldsymbol{P}_t)}{\partial \boldsymbol{K}_t}=&\frac{\partial [tr(\boldsymbol{P}_{t|t-1}) -2tr(\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{P}_{t|t-1})+ tr(\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{P}_{t|t-1}\boldsymbol{H}_t^T\boldsymbol{K}_t^T)+tr(\boldsymbol{K}_t \boldsymbol{R}_t\boldsymbol{K}_t^T)]}{\partial \boldsymbol{K}_t} \\ =& 0-2(\boldsymbol{H}_t\boldsymbol{P}_{t|t-1})^T+2(\boldsymbol{K}_t\boldsymbol{H}_t\boldsymbol{P}_{t|t-1}\boldsymbol{H}_t^T)+2(\boldsymbol{K}_t \boldsymbol{R}_t) ~~\left(\text{Accroding to the property that }\frac{\partial tr(\boldsymbol{A}\boldsymbol{B})}{\partial \boldsymbol{A}}=\boldsymbol{B}^T, \frac{\partial tr(\boldsymbol{A}\boldsymbol{B}\boldsymbol{A}^T)}{\partial \boldsymbol{A}}=2\boldsymbol{A}\boldsymbol{B}\right) \end{aligned} \] 令上式等于0,可得: \[ \boldsymbol{K}_t=\boldsymbol{P}_{t|t-1}^T\boldsymbol{H}_t^T(\boldsymbol{R}_t+\boldsymbol{H}_t\boldsymbol{P}_{t|t-1}\boldsymbol{H}_t^T)^{-1} \]
正态分布相乘
由于\(t\)时刻模型的预测值和系统的测量值都满足正态分布,因此一个直接的想法就是把两个正态分布的概率密度函数相乘,从而得到系统的最佳估计。两个正态分布的乘积仍然是一个正态分布,因此卡尔曼滤波过程便可以一直迭代下去。
以一维为例,我们假设有两个正态分布函数,\(y_1\)对应于模型的预测,\(y_2\)对应于观测: \[ y_1(r;\mu_1,\sigma_1,c)=\frac{1}{\sqrt{2\pi (\frac{\sigma_1}{c})^2}}\exp (-\frac{(r-(\frac{\mu_1}{c}))^2}{2(\frac{\sigma_1}{c})^2}) \\ y_2(r;\mu_2,\sigma_2)=\frac{1}{\sqrt{2\pi \sigma_2^2}}\exp (-\frac{(r-\mu_2)^2}{2\sigma_2^2}) \\ \] 其中,参数\(c\)是为了将模型预测值对应的函数空间映射到观测值对应的函数空间。二者相乘并归一化之后的概率分布函数为: \[ y_{\text{fused}}(r;\mu_{\text{fused}},\sigma_{\text{fused}})=\frac{1}{\sqrt{2\pi \sigma_{\text{fused}}^2}}\exp (-\frac{(r-\mu_{\text{fused}})^2}{2\sigma_{\text{fused}}^2}) \\ \] 其中, \[ \mu_{\text{fused}} = \mu_1 +\left(\frac{\frac{\mu_1^2}{c}}{(\frac{\sigma_1}{c})^2+\sigma_2^2}\right)\left(\mu_2-\frac{\mu_1}{c}\right) \\ \sigma_{\text{fused}}^2=\sigma_1^2-\left(\frac{\frac{\mu_1^2}{c}}{(\frac{\sigma_1}{c})^2+\sigma_2^2}\right)\frac{\mu_1^2}{c} \] 卡尔曼滤波公式中的参数与上式中的对应关系如下: \[ \begin{aligned} \mu_{\text{fused}} &\rightarrow \hat{\boldsymbol{x}}_{t|t} \\ \mu_{\text{1}} &\rightarrow \hat{\boldsymbol{x}}_{t|t-1} \\ \mu_{\text{2}} &\rightarrow {\boldsymbol{z}}_{t} \\ \sigma_{\text{fused}}^2 &\rightarrow \boldsymbol{P}_{t|t}\\ \sigma_{\text{1}}^2 &\rightarrow \boldsymbol{P}_{t|t-1}\\ \sigma_{\text{2}}^2 &\rightarrow \boldsymbol{R}_{t}\\ \frac{1}{c} &\rightarrow \boldsymbol{H}_t\\ \left(\frac{\frac{\mu_1^2}{c}}{(\frac{\sigma_1}{c})^2+\sigma_2^2}\right) &\rightarrow \boldsymbol{K}_t\\ \end{aligned} \] 以二维的卡尔曼滤波为例,测量值和模型预测值的正态分布融合过程可以表示为下图:
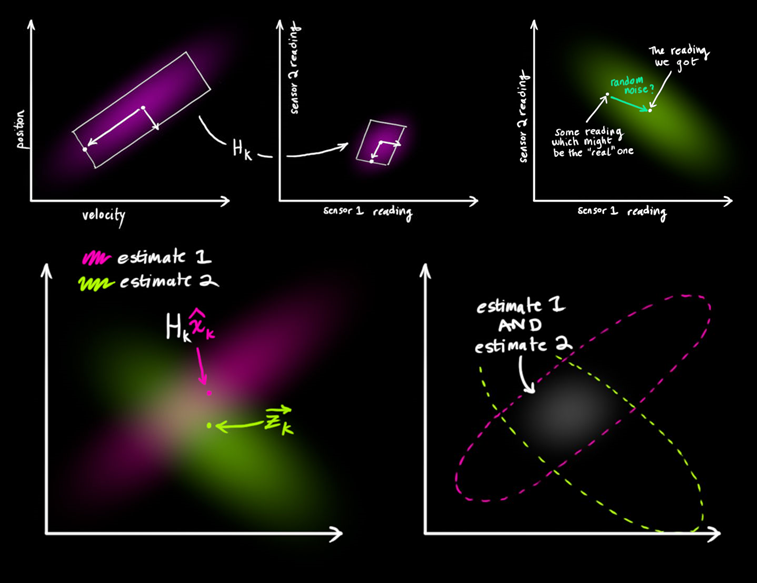
程序示例
1 | import numpy as np |
1 | class KalmanFilter: |
以一维平面小车的运动为例,小车的状态包括位置、速度和加速度三个量,即\(x=\begin{pmatrix}p \\ v \\a \end{pmatrix}\)。根据物理定律,假设时间间隔为1,那么转移矩阵可以写为\(F=\begin{pmatrix} 1 & 1 & \frac{1}{2} \\ 0 & 1 & 1 \\0 & 0 & 1 \end{pmatrix}\)。为了简便起见,我们假设测量值只有位置信息,也就是说\(H=\begin{pmatrix} 1 & 0 & 0 \end{pmatrix}\),但是测量值也不一定准确,满足方差确定的正态分布。同时,假设我们可以控制小车的油门和刹车,它们会直接影响小车的加速度。也就是说,矩阵\(u=\begin{pmatrix} t \\b \end{pmatrix}\),\(B=\begin{pmatrix} 0 & 0 \\ 0 & 0 \\1 & -1 \end{pmatrix}\)。
为了简便,我们假设小车的所有阻力为0。此外,我们假设协方差矩阵\(Q\)为零矩阵,传感器测量值的噪声标准差为1。小车初始时在原点处静止。
根据上述内容,我们便可以构造用于获取小车位置的卡尔曼滤波器。
1 | F=np.array(((1.0,1.0,0.5),(0.0,1.0,1.0),(0.0,0.0,1.0))) |
1 | car_kalman_filter=KalmanFilter(F,B,H,Q,R,np.array([[0.0],[0.0],[0.0]])) |
假设在\(t=1\)时,我们踩了一下油门,给了小车一个数值为0.5的加速度。但是由于各种因素的影响,在小车身上产生的实际加速度并不是0.5,而是一个在0.5附近的数字。而卡尔曼滤波则会通过并不是很准确的观察值,对加速度的值进行修正。
1 | status_vector=list() |
1 | acceleration_1=0.5+0.3*np.random.randn(1) |
1 | acceleration_1 |
array([0.20577584])1 | position_1=0+2.0*np.random.randn(1) #位置的测量值 |
1 | status_vector.append(status) |
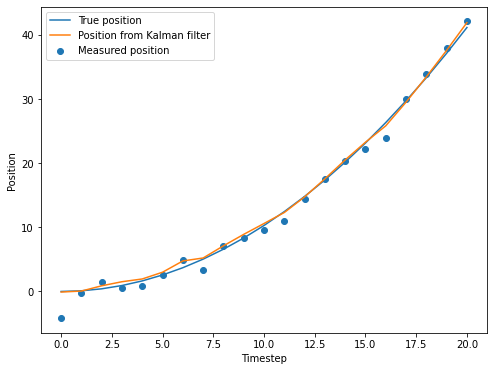
保持状态不变,迭代20次。从结果中可以看出,虽然卡尔曼滤波器在开始时的加速度并不准确,但是随着迭代过程的进行,滤波器会使用位置的测量信息,对加速度进行修正。在迭代20轮之后,加速度的值已经很接近真实值。
1 | for i in range(20): |
1 | figure=plt.figure(figsize=(8,6)) |
1 | figure=plt.figure(figsize=(8,6)) |
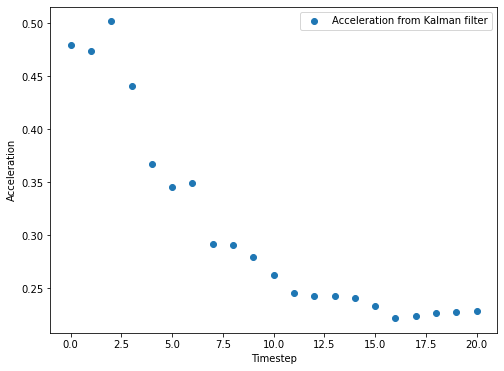
参考
- https://courses.engr.illinois.edu/ece420/sp2017/UnderstandingKalmanFilter.pdf
- How a Kalman filter works, in pictures | Bzarg
- 如何通俗并尽可能详细地解释卡尔曼滤波? - 知乎 (zhihu.com)
- 贝叶斯视角下的卡尔曼滤波 - 知乎 (zhihu.com)
- [卡尔曼滤波器详解(三):数学推导_@清欢_-CSDN博客](https://blog.csdn.net/weixin_46581517/article/details/107706149)
