深度学习-图神经网络概述

注：本文的内容主要来自于三篇图神经网络综述文章A Comprehensive Survey on Graph Neural Networks，Graph neural networks: A review of methods and applications和Deep Learning on Graphs: A Survey的总结。

概述

传统的卷积神经网络、循环神经网络等结构在提取欧氏空间数据（例如语音、图像、自然语言等结构化的序列或者网格数据）的特征上面取得了巨大的成功。但是实际许多应用场景的数据是从非欧氏空间产生的，例如社交网络、知识图谱、分子结构等。相比于文本和图像，这些非结构化的图结构数据比较复杂，例如结点数量任意且顺序不固定、结点之间的关系复杂、可能包含多模态的特征等。

因此，图数据的复杂性给传统的机器学习算法带来了很大挑战。一些对于欧氏数据的运算（如卷积）不能直接应用在图结构上。为了将深度学习方法应用到图结构数据上，图神经网络（Graph Neural Network，GNN）便由此出现并不断发展。

图神经网络的概念最早出现在2005年，早期的图神经网络研究主要是使用循环神经网络结构，通过聚合相邻结点信息并重复迭代至稳定状态的方式，学得结点的特征向量表示。这种方法的计算开销很大，而且网络的表达能力和可扩展性都比较差。

在此之后，图神经网络的发展主要受到两个研究领域的启发。一是卷积神经网络，由于卷积神经网络在计算机视觉领域取得了巨大成功，一些学者受图像卷积操作的启发，为图结构重新定义了卷积操作。二是图表示学习，即学习图中的结点、边或者子图结构的低维向量表示，相关的研究包括DeepWalk、node2vec、LINE等。基于这两个领域的研究，后面出现了许多图神经网络的变体。

分类

按照不同的分类规则，可以将图神经网络分成多种不同的类别。这里我们取A Comprehensive Survey on Graph Neural Networks这篇综述里面的分类：

• 循环图神经网络（Recurrent Graph Neural Network）：通过使用循环神经网络的结构，学习结点的表示（Representation）。图中的每个结点都在不断地与自己的相邻结点交换信息，直到最终达到一个平衡态。而这里面消息传递的思想也被基于空域的图卷积操作所使用。
• 卷积图神经网络（Convolutional Graph Neural Network）：图结构上的卷积操作是将欧式数据的卷积操作进一步泛化到图结构中。它的主要思想是通过聚合结点自己及其相邻结点的特征，从而得到结点的表示。循环图神经网络与卷积图神经网络的不同之处在于，图卷积操作通常会搭建很多层，每一层的模型参数都不相同；而循环图神经网络则是与循环神经网络类似，在每一步迭代的过程中使用的是相同的模型参数。
• 图自编码器（Graph Autoencoder）：与传统的自编码器类似，图自编码器将结点或图编码到一个向量空间内，然后通过编码信息对图进行重建。图编码器结构可以学习到图结构的嵌入表示，也可以将其应用于图结构的生成。
• 时空图神经网络（Spatial-temporal Graph Neural Network）：一些场景中的图是在时域和空域都连续变化的动态图，例如交通网络，人体动作等。时空图神经网络的目的是从这类图中学习到其中的隐藏特征。对于时空图神经网络来说，需要同时考虑时域和空域的依赖性，目前使用较多的方法是用图卷积操作提取空域的特征，同时结合RNN或者CNN去提取时域的特征。

设计路线

图神经网络的基本设计路线大致分为如下几个部分：

1. 建立图结构：根据实际应用，使用原始数据建立图结构。在一些应用场景中，图结构是显式的，例如分子、知识图谱等；而也有一些应用场景中，存在着隐式的图结构，例如根据文本或者图像之间的关系去构造图结构。

2. 确定图的种类：实际应用中抽象出的图结构可以进一步进行分类，按照边是否有方向分为有向/无向图、按照结点和边的类型是否相同分为同构/异构图、按照图是否随着时间变化分为静态/动态图。后续在选择网络结构的时候便需要考虑这些不同的分类。

3. 设计损失函数：损失函数的设置需要针对于任务类型以及训练集是否有标签。图结构的学习任务通常可以分为三种：关于结点的任务（例如结点的分类/回归任务）、边级别的任务（例如边的分类或者边的连接预测）、以及图级别的任务（例如图的分类/回归任务）。按照训练集的数据是否有标签也可以分为监督学习、半监督学习和非监督学习。损失函数需要综合考虑以上两点去设计。

   例如对于图分类的任务，则可以使用交叉熵损失函数；而对于图自编码器，则使用的是基于图结构的重建损失（例如比较邻接矩阵的相似度、比较结点相似度等）；如果要使用GAN去生成图结构，则需要为图结构专门设计判别器和生成器对抗训练的损失函数。

4. 建立模型：图神经网络由不同的计算模块组合而成，常用的计算模块包括聚合模块、采样模块和池化模块。聚合模块用于聚合结点的信息；当图的规模比较大时，采样模块可以对聚合操作进行一定的约束；池化模块则是用于从结点中获取整幅图或者子图的信息。

上述的设计路线可以涵盖大部分的GNN模型。下文将对一些图神经网络中常用的模块进行介绍。

组成模块

聚合模块

图神经网络的聚合模块大体可以分为三类：卷积运算（Convolutional Operator）、循环运算（Recurrent Operator）和跳跃连接（Skip Connection）。下图为聚合模块的分类以及每一类中的例子：

卷积运算

卷积运算是图神经网络中应用最广泛的一种聚合运算，主要分为两大类：基于频域（Spectral）的方法和基于空域（Spatial）的方法。基于频域方法的理论来源于图结构的信号处理，在频域空间定义图的卷积操作；而基于空域的方法则依据图的拓扑结构，直接在图结构上定义卷积运算。在这两大类方法中又有许多不同种类的变体。

基于频域的图卷积运算先使用图傅里叶变换\(\mathscr{F}(\boldsymbol{x})=\boldsymbol{U}^T\boldsymbol{x}\)，将一个图上的信号\(\boldsymbol{x}\)转换到频域，并在频域上面进行卷积运算。之后再使用逆变换\(\mathscr{F}^{-1}(\boldsymbol{x})=\boldsymbol{U}\boldsymbol{x}\)将运算后的结果从频域空间转换回来。其中，\(\boldsymbol{U}\)是图拉普拉斯算子\(\boldsymbol{L}=\boldsymbol{I}_N-\boldsymbol{D}^{-\frac{1}{2}}\boldsymbol{A}\boldsymbol{D}^{-\frac{1}{2}}\)的特征向量矩阵，即通过计算\(\boldsymbol{L}\)的特征值分解\(\boldsymbol{L}=\boldsymbol{U}\boldsymbol{\Lambda} \boldsymbol{U}^T\)可得到\(\boldsymbol{U}\)。

图结构上的卷积操作被定义为： \[ \begin{aligned} \boldsymbol{g} \star \boldsymbol{x} =& \mathscr{F}^{-1}(\mathscr{F}(\boldsymbol{g})\odot\mathscr{F}(\boldsymbol{x})) \\ =&\boldsymbol{U}(\boldsymbol{U}^T\boldsymbol{g}\odot\boldsymbol{U}^{T}\boldsymbol{x}) \end{aligned} \] 其中，\(\boldsymbol{U}^T\boldsymbol{g}\)是在频域内的滤波器（filter）。如果我们简化运算，将滤波器使用一个可学习的对角矩阵\(\boldsymbol{g}_w\)代替，那么基于频域图卷积运算的基本方程便可以写成下面的格式： \[ \boldsymbol{g}_w \star \boldsymbol{x} = \boldsymbol{U}\boldsymbol{g}_w \boldsymbol{U}^{T}\boldsymbol{x} \] 而通过设计不同的\(\boldsymbol{g}_w\)，便有了一系列基于频域图卷积运算的变体。

基于空域的图卷积运算则是直接在图上定义卷积运算，每个结点通过聚合相邻结点的信息来更新自己的信息。对于空域的图卷积运算，可以用MPNN框架来描述大部分的运算操作： \[ \boldsymbol{x}_u^{l+1}=U^{l+1}(\boldsymbol{x}_u^l,\sum_{v\in N(u)}M^{l+1}(\boldsymbol{x}_u^l,\boldsymbol{x}_v^l,\boldsymbol{e}_{uv}^l)) \] 其中，\(M\)和\(U\)分别代表消息传递和状态更新操作，\(\boldsymbol{x}\)代表结点的特征向量，\(\boldsymbol{e}\)代表边的特征向量，上标\(l\)代表图卷积运算的层数。

循环运算

循环运算在图神经网络的研究中最早出现，它与图卷积运算的主要不同点在于，每一层图卷积运算都拥有自己的权重，而每一层的循环运算是共享权重的。循环运算也分为两大类，一类是基于不动点理论的收敛方法，另一类则是基于门控单元的方法。

收敛方法需要通过不断地迭代，直到每个结点的特征向量不再变化，因此通常有很大的计算开销。最早的图神经网络（即图中的\(\underline{\text{GNN}}\)）使用的是如下的计算公式： \[ \boldsymbol{h}_{u}^{l+1}=\sum_{v\in N(u)}f(\boldsymbol{x}_{u},\boldsymbol{x}_{v},\boldsymbol{e}_{uv},\boldsymbol{h}_{v}^{l}) \]

其中\(f\)是个含有参数的函数，\(\boldsymbol{h}_{u}^{l}\)代表结点\(u\)在经过\(l\)次迭代之后的隐藏状态，而\(l=0\)的初始状态则是随机生成的。由于最终要求隐藏结点的状态能够收敛，因此\(f\)必须是个收缩的映射（即两个结点之间的距离在经过函数映射之后会变得更小）。

而基于门控单元的方法在聚合运算中使用GRU或者LSTM门控单元，从而在图结构的多次聚合运算之后仍然能够保留一些长期记忆的信息。这种方法在训练时只会进行固定次数的聚合运算，因此并不保证最终能够收敛。例如GGNN（Gated Graph Neural Network）使用GRU单元进行循环运算： \[ \boldsymbol{h}_{u}^{l+1}=\text{GRU}(\boldsymbol{h}_{u}^{l},\sum_{v\in N(u)}\boldsymbol{W}\boldsymbol{h}_{v}^{l}) \] 而初始状态\(\boldsymbol{h}_{u}^{0}=\boldsymbol{x}_{u}\)。

跳跃连接

跳跃连接主要是为了解决图神经网络在聚合运算中的一系列问题。对于图神经网络来说，更深的网络结构并不意味着更好的结果，甚至可能会使得结果更糟糕。这是因为每个结点上都带有一定的噪声信息，多层的聚合操作也使得这些噪声信息将以指数级别的增长规律在相邻结点之间传递。而更深的层数也会使得每个结点的特征向量更加相似，从而导致过平滑的问题。

顾名思义，跳跃连接指的是在图神经网络的结构中引入类似于ResNet的残差结构，实现层与层之间的跳跃连接，从而使得网络的层数可以变得更深。下面为Jumping Knowledge Network的结构示意图：

采样模块

在GNN的聚合操作中，每个结点都会从它的相邻结点中聚合信息。从定性的角度去思考，在做完一次聚合操作之后，每个结点已经包含了它相邻结点的信息。因此在做第二次聚合操作的时候，相当于每个结点都能间接地接收到与自身“距离”为2（即两结点之间经过两条边可以到达）的所有结点的信息。以此类推，随着聚合操作层数的增加，对一个结点的信息更新有影响的结点数目也将以指数级别增加。此外，当图的规模很大时，如果要处理一个结点所有相邻结点的信息，将会带来极大的计算开销。因此，需要在图神经网络中引入一些采样的手段以解决上述这些问题。

采样模块可以分为三种不同的类型：结点采样（Node Sampling）、层采样（Layer Sampling）和子图采样（Subgraph Sampling）。下面为采样模块分类的一个示意图：

• 结点采样：对于每个结点，都从它所有的相邻结点中进行下采样，得到一个相邻结点的子集
• 层采样：在每一层中，只保留部分结点做聚合操作
• 子图采样：从整个图结构中采样出若干个子图，然后将相邻结点的搜索限制在这些子图中

池化模块

在得到了结点特征之后，可以按照一定规则将所有结点的信息聚合为一个特征向量，从而进一步得到图的特征表示，这一操作被称为池化（Pooling），也被称作读出（Readout）操作。图的池化操作是顺序无关的，也就是说如果将结点的编号随机打乱，最终得到的图的特征表示应当也不变。

在图神经网络中，池化模块分为直接池化（Direct Pooling）和层次池化（Hierarchical Pooling），可总结为下图：

直接池化

直接池化指的是按照不同的结点选择策略，从结点的特征中直接获取图的特征。主要包含以下几种：

• 统计计算：指的是对所有结点的特征进行\(\max\)，\(\text{sum}\)或者\(\text{avg}\)三种统计计算的其中之一，获得图结构的全局特征表示。用公式则可以分别写为： \[ \begin{aligned} \boldsymbol{r}=&\text{max}_{n=1}^{N} \boldsymbol{x}_n \\ \boldsymbol{r}=&\sum_{n=1}^{N} \boldsymbol{x}_n \\ \boldsymbol{r}=&\frac{1}{N}\sum_{n=1}^{N} \boldsymbol{x}_n \\ \end{aligned} \] 其中，\(\boldsymbol{x}_n\)代表第\(n\)个结点的特征向量。

• Attention：基于Attention机制做如下计算： \[ \boldsymbol{r}=\sum_{n=1}^{N}\text{softmax}(h_{\text{gate}}(\boldsymbol{x}_n)) \odot h_{\Theta}(\boldsymbol{x}_n) \] 其中，\(h_{\text{gate}}\)和\(h_{\Theta}\)代表两个不同的神经网络，\(\boldsymbol{x}_n\)代表第\(n\)个结点的特征向量。

• Set2set：这一操作出现在MPNN中，它基于LSTM单元进行固定次数的运算，从而获得图结构的特征。计算公式如下： \[ \begin{aligned} \boldsymbol{q}_t=&\text{LSTM}(\boldsymbol{q}_{t-1}^*) \\ \alpha_{i,t}=&\text{softmax}(\boldsymbol{x}_i \cdot \boldsymbol{q}_t) \\ \boldsymbol{r}_t=&\sum_{i=1}^{N}\alpha_{i,t}\boldsymbol{x}_i \\ \boldsymbol{q}_t^*=&\boldsymbol{q}_t||\boldsymbol{r}_t \end{aligned} \] 其中，\(\boldsymbol{x}_i\)代表第\(i\)个结点的特征向量，\(t\)代表上述操作重复执行的次数。Set2set操作最终的输出为\(\boldsymbol{q}_t^*\)。

• SortPooling：按照一定规则对结点进行排序，然后依据排序后的结点特征得到图结构的特征。最简单的办法是排序之后选出排在前\(k\)个的结点作为图的表示。

层次池化

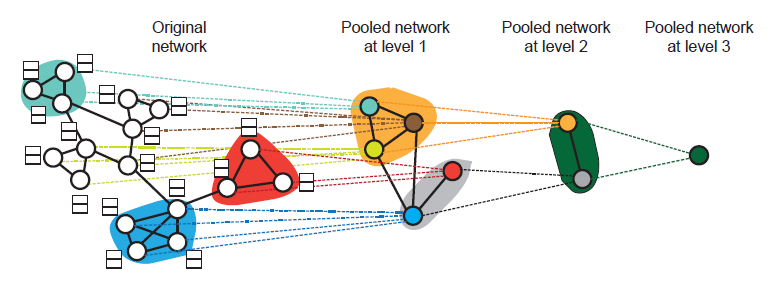
层次池化指的是在池化操作的时候分成多级计算，通过多层操作最终得到图的特征表示。如下图便是使用层次聚类的方法进行层次池化操作的一个示意图：

image-20210717155311031

应用

目前，图神经网络已经在不同领域得到广泛应用，下面简单地列出一些相关的例子。

• 计算机视觉：将LiDAR拍摄到的点云进行分类与分割；识别图像中物体的关联性；识别人体的动作等
• 自然语言处理：基于语义关系图进行文本分类、生成句子；以及基于句子生成相应的语义关系图等
• 交通：使用时空图神经网络预测交通流量
• 化学：化学反应预测；生成分子指纹；预测分子性质；蛋白质性质预测；等等
• 其它：物理建模；知识图谱；等等

参考

1. 图神经网络从入门到入门 - 知乎 (zhihu.com)
2. 如何理解 Graph Convolutional Network（GCN）？ - 知乎 (zhihu.com)
3. Wu, Z. et al. A Comprehensive Survey on Graph Neural Networks.
4. Zhou, J. et al. Graph neural networks: A review of methods and applications.
5. Zhang, Z., Cui, P. & Zhu, W. Deep Learning on Graphs: A Survey.
6. 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (一) - SivilTaram - 博客园 (cnblogs.com)