概述

自编码器是神经网络的一种，经过训练后能尝试将输入复制到输出。这个网络可以看作由两部分组成：一个由函数\(\boldsymbol{h}=f(\boldsymbol{x})\)表示的编码器，和一个生成重构的解码器\(\boldsymbol{r}=g(\boldsymbol{h})\)。其中，\(f()\)和\(g()\)分别表示编码器和解码器所对应神经网络的函数表达式。

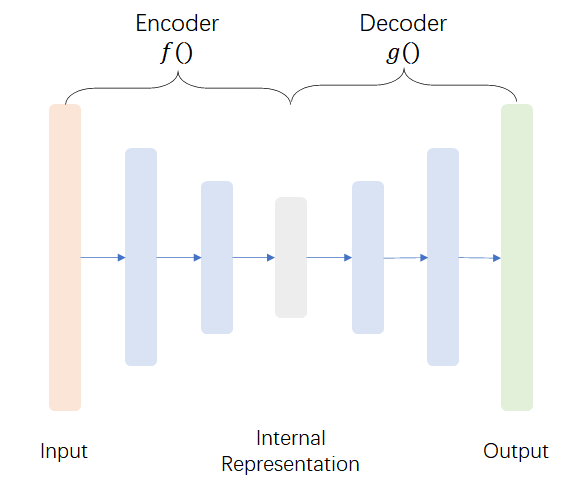
需要注意的是，如果一个自编码器只是简单地学会将处处设置为\(g(f(\boldsymbol{x}))=\boldsymbol{x}\)，那么这个自编码器就没有什么特别的用处，且不能被推广到新的实例。相反，通常是向自编码器强加一些约束，使它只能近似地复制，并且只能复制与训练数据相似的输入。这种约束强制模型考虑输入数据的哪些部分需要被优先复制，这样往往可以学到数据的有用特性。

目前，自编码器的应用主要包括降维、特征学习、去噪、图像生成、异常检测等。

欠完备自编码器

从自编码器中获得有用特征的一种方法是限制\(\boldsymbol{h}\)的维度比\(\boldsymbol{x}\)小，这种编码维度小于输入维度的自编码器称为欠完备自编码器。相应地，如果允许隐藏编码的维数与输入相等，或者隐藏编码维数大于输入，则被称为过完备自编码器，而在这种情况下，即使是线性编码器和线性解码器也可以学会将输入复制到输出，而学不到任何有关数据分布的有用信息。

学习欠完备的表示将强制自编码器捕捉到训练数据中最显著的特征。学习过程可以简单地描述为最小化如下的损失函数： \[ L(\boldsymbol{x},g(f(\boldsymbol{x}))) \] 其中\(L\)代指损失函数，用于惩罚\(g(f(\boldsymbol{x}))\)和\(\boldsymbol{x}\)的差异，如均方误差。

如果解码器是线性的，且\(L\)为均方误差，则欠完备自编码器会学习出与PCA相同的生成子空间。这种情况下，自编码器在训练去执行复制任务的时候，同时会学到训练数据的主元子空间。因此，拥有非线性编码器函数\(f\)和非线性解码器函数\(g\)的自编码器能够学习出更强大的PCA非线性推广。但是，如果编码器和解码器的容量太大（或者说它们的参数太多从而导致近似能力太强），则自编码器仅仅会执行复制任务而捕捉不到任何有关数据分布的有用信息。

正则自编码器

概述

正则自编码器使用的损失函数鼓励模型除了将输入复制到输出之外，可以学习到一些其它特性，而不必限制使用浅层的编码器和解码器以及小的编码维数来限制模型的容量。即使模型容量大到足以学习一个无意义的恒等函数，非线性且过完备的正则自编码器仍然能够从数据中学到一些关于数据分布的有用信息。

下面介绍几种不同的正则自编码器。

稀疏自编码器

稀疏自编码器简单地在训练时结合编码层的稀疏惩罚\(\Omega(\boldsymbol{h})\)和重构误差： \[ L(\boldsymbol{x},g(f(\boldsymbol{x})))+\Omega(\boldsymbol{h}) \] 其中，惩罚项\(\Omega(\boldsymbol{h})\)可以被视为加到前馈网络的正则项。这里的惩罚项可以有多种选择，例如L1/L2正则化，KL散度等。

备注：使用KL散度的损失函数表达式

KL散度即相对熵=交叉熵-信息熵： \[ KL(P||Q)=H(P,Q)-H(P)=\sum_{k=1}^{N}p_k\log (\frac{1}{q_k})-\sum_{k=1}^{N}p_k\log (\frac{1}{p_k})=\sum_{k=1}^{N}p_k\log (\frac{p_k}{q_k}) \] 其中，\(p_k\)和\(q_k\)对应于离散概率分布\(P\)和\(Q\)中的第\(k\)项

而将KL散度应用到稀疏自编码器中，损失函数的表达式可以写为： \[ L(\boldsymbol{x},g(f(\boldsymbol{x})))+\Omega(\boldsymbol{h})+\beta\sum_{j=1}^{s}KL(\rho ||\hat{\rho}_j) \] 其中KL散度的表达式为： \[ KL(\rho ||\hat{\rho}_j)=\rho \log \frac{\rho}{\hat{\rho}_j}+(1-\rho)\frac{1-\rho}{1-\hat{\rho}_j} \] 在上式中，\(\rho\)代表我们所期望的平均激活值，需要手动设置；而\(\hat{\rho}_j=\frac{1}{m}\sum_{i=1}^{m}[a_{j}(\boldsymbol{x}_i)]\)，\(m\)代表输入数据的个数，\(a_j(\boldsymbol{x}_i)\)代表第\(i\)个输入数据在编码器最后一层的第\(j\)个神经元所产生的激活值。

稀疏自编码器一般用来学习特征，以便用于像分类这样的任务。稀疏正则化的自编码器必须反映训练数据集的独特统计特征，而不是简单地充当恒等函数。

去噪自编码器

去噪自编码器（Denoising Autoencoder，DAE）是一类接受损坏数据作为输入，并训练来预测原始未被损坏数据作为输出的编码器。在去噪自编码器中，编码函数\(f(\boldsymbol{x})\)的概念被推广到编码分布\(p_{\text{encoder}}(\boldsymbol{h}|\boldsymbol{x})\)。任何潜变量模型\(p_{\text{model}}(\boldsymbol{h}, \boldsymbol{x})\)定义了一个随机编码器\(p_{\text{encoder}}(\boldsymbol{h}|\boldsymbol{x})=p_{\text{model}}(\boldsymbol{h}|\boldsymbol{x})\)和随机解码器\(p_{\text{decoder}}(\boldsymbol{x}|\boldsymbol{h})=p_{\text{model}}(\boldsymbol{x}|\boldsymbol{h})\)。

在DAE的训练过程中，需要引入一个损坏过程\(C(\tilde{\boldsymbol{x}}|\boldsymbol{x})\)，这个条件分布代表给定数据样本\(\boldsymbol{x}\)产生损坏样本\(\tilde{\boldsymbol{x}}\)的概率。自编码器按照下面的过程，从训练数据对\((\tilde{\boldsymbol{x}},\boldsymbol{x})\)中学习一个重构分布\(p_{\text{reconstruct}}(\boldsymbol{x}|\boldsymbol{\tilde{x}})\)：

从训练数据中采集一个训练样本\(\boldsymbol{x}\)
从\(C(\tilde{\boldsymbol{x}}|\boldsymbol{x})\)中采集一个损坏样本\(\boldsymbol{\tilde{x}}\)，\(C\)通常为二项分布
将\((\tilde{\boldsymbol{x}},\boldsymbol{x})\)作为训练样本来估计自编码器的重构分布\(p_{\text{reconstruct}}(\boldsymbol{x}|\boldsymbol{\tilde{x}})=p_{\text{decoder}}(\boldsymbol{x}|\boldsymbol{h})\)，其中\(\boldsymbol{h}\)为编码器\(f(\boldsymbol{\tilde{x}})\)的输出，\(p_{\text{decoder}}\)根据解码函数\(g(\boldsymbol{h})\)定义
最小化损失函数\(L\)，损失函数可以为平方损失函数或者交叉熵。

收缩自编码器

另一个正则化自编码器的策略是使用一个类似于稀疏自编码器中的惩罚项\(\Omega\)，此时损失函数为： \[ L(\boldsymbol{x},g(f(\boldsymbol{x})))+\Omega(\boldsymbol{h},\boldsymbol{x}) \] 其中，\(\Omega(\boldsymbol{h},\boldsymbol{x})=\lambda\sum_{i}||\nabla_\boldsymbol{x}\boldsymbol{h}_i||^2=\lambda ||\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}||^2_F\)。\(F\)代表Frobenius范数。这迫使模型学习一个在\(\boldsymbol{x}\)变化小时，目标也没有太大变化的函数。因为这个惩罚只对训练数据适用，它迫使自编码器学习可以反映训练数据分布信息的特征。

收缩惩罚迫使自编码器学习到的所有映射对于输入的梯度都很小，即把输入都降维到一个很小的区域（点附近）；而重构误差迫使自编码器学习一个恒等映射，保留完整的信息。在这两种惩罚的作用下，使得大部分映射对于输入的梯度都很小，而只有少部分的大梯度。这样在输入具有小扰动时，小梯度会减小这些扰动，达到增加自编码器对输入附近小扰动的鲁棒性。

变分自编码器

原理

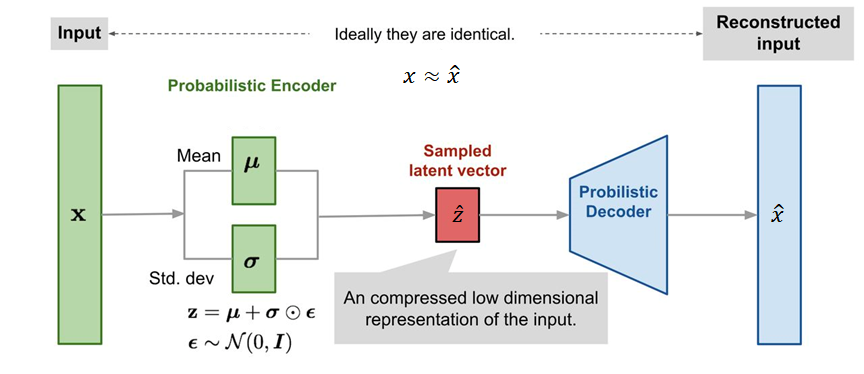
像标准自编码器一样，变分自编码器（Variational AutoEncoder，VAE）是一种由编码器和解码器组成的结构，经过训练以使编码解码后的数据与初始数据之间的重构误差最小。但是，为了引入隐空间的某些正则化，我们对编码-解码过程进行了一些修改：我们不是将输入编码为隐空间中的单个点，而是将其编码为隐空间中的概率分布。

VAE的模型训练过程如下：

使用编码器，将输入\(\boldsymbol{x}\)编码为隐空间上的分布\(q(\boldsymbol{z}|\boldsymbol{x})\)
从该分布中采样隐空间中的一个点\(\hat{\boldsymbol{z}}\sim q(\boldsymbol{z}|\boldsymbol{x})\)
使用解码器对采样点\(\hat{\boldsymbol{z}}\)进行解码，得到\(\boldsymbol{x}\)的重建\(\hat{\boldsymbol{x}}\)
计算重建误差，并通过反向传播更新网络参数

实践中，通常选择高斯分布作为编码的分布，这样网络的结构便如下图所示。其中，由于随机采样过程必须允许误差可以反向传播，因此随机采样这一步骤使用重参数化技巧进行表达：\(\boldsymbol{z}=\boldsymbol{\mu}+\boldsymbol{\sigma}\odot \boldsymbol{\epsilon}\)，\(\boldsymbol{\epsilon}\sim \mathcal{N}(0,\boldsymbol{I})\)。这样，均值和协方差向量便可以进行反向传播。

损失函数

根据贝叶斯定理，可得后验概率表达式：\(p(\boldsymbol{z}|\boldsymbol{x})=\frac{p(\boldsymbol{x}|\boldsymbol{z})p(\boldsymbol{z})}{p(\boldsymbol{x})}\)，但是实际中\(p(\boldsymbol{x})\)无法计算，因而这个后验概率表达式不可解。

由全概率公式可得：\(p(\boldsymbol{x})=\int p(\boldsymbol{x}|\boldsymbol{z})p(\boldsymbol{z})d\boldsymbol{z}\)，而如果\(\boldsymbol{z}\)是一个维度很高的变量，则将变为一个多重积分式，难以计算。而变分自编码器的思想是使用一个可解的分布\(q(\boldsymbol{z}|\boldsymbol{x})\)去近似\(p(\boldsymbol{z}|\boldsymbol{x})\)，并希望二者的差距越小越好，也就是说二者的KL散度越小越好。因此，损失函数 \[ L=\min KL(q(\boldsymbol{z}|\boldsymbol{x})||p(\boldsymbol{z}|\boldsymbol{x})) \] 根据KL散度的定义，可得： \[ \begin{aligned} KL(q(\boldsymbol{z}|\boldsymbol{x})||p(\boldsymbol{z}|\boldsymbol{x}))=&\int q(\boldsymbol{z}|\boldsymbol{x}) \log \frac{q(\boldsymbol{z}|\boldsymbol{x})}{p(\boldsymbol{z}|\boldsymbol{x})}d\boldsymbol{z} \\ =&\int q(\boldsymbol{z}|\boldsymbol{x})\log \frac{q(\boldsymbol{z}|\boldsymbol{x})}{\frac{p(\boldsymbol{x}|\boldsymbol{z})p(\boldsymbol{z})}{p(\boldsymbol{x})}}d\boldsymbol{z} \\ =& \int q(\boldsymbol{z}|\boldsymbol{x}) \log q(\boldsymbol{z}|\boldsymbol{x})d\boldsymbol{z}+\int q(\boldsymbol{z}|\boldsymbol{x}) \log p(\boldsymbol{x})d\boldsymbol{z}-\int q(\boldsymbol{z}|\boldsymbol{x}) \log [p(\boldsymbol{x}|\boldsymbol{z})p(\boldsymbol{z})]d\boldsymbol{z} \\ =& \int q(\boldsymbol{z}|\boldsymbol{x}) \log q(\boldsymbol{z}|\boldsymbol{x})d\boldsymbol{z}+\log p(\boldsymbol{x})-\int q(\boldsymbol{z}|\boldsymbol{x}) \log [p(\boldsymbol{x}|\boldsymbol{z})p(\boldsymbol{z})]d\boldsymbol{z} \\ \end{aligned} \] 由于\(\log p(\boldsymbol{x})\)是个定值，因此最小化\(KL(q(\boldsymbol{z}|\boldsymbol{x})||p(\boldsymbol{z}|\boldsymbol{x}))\)其实相当于计算如下表达式： \[ \begin{aligned} & \min \int q(\boldsymbol{z}|\boldsymbol{x}) \log q(\boldsymbol{z}|\boldsymbol{x})d\boldsymbol{z}-\int q(\boldsymbol{z}|\boldsymbol{x}) \log [p(\boldsymbol{x}|\boldsymbol{z})p(\boldsymbol{z})]d\boldsymbol{z} \\ =&\min \int q(\boldsymbol{z}|\boldsymbol{x}) \log q(\boldsymbol{z}|\boldsymbol{x})d\boldsymbol{z}-\int q(\boldsymbol{z}|\boldsymbol{x}) \log p(\boldsymbol{x}|\boldsymbol{z})d\boldsymbol{z}-\int q(\boldsymbol{z}|\boldsymbol{x}) \log p(\boldsymbol{z})d\boldsymbol{z} \\ =&\min \int q(\boldsymbol{z}|\boldsymbol{x}) \log \frac{q(\boldsymbol{z}|\boldsymbol{x})}{p(\boldsymbol{z})}d\boldsymbol{z}-\int q(\boldsymbol{z}|\boldsymbol{x}) \log p(\boldsymbol{x}|\boldsymbol{z})d\boldsymbol{z} \\ =&\min KL(q(\boldsymbol{z}|\boldsymbol{x})||p(\boldsymbol{z}))-E_{\boldsymbol{z}\sim q(\boldsymbol{z}|\boldsymbol{x})}[\log p(\boldsymbol{x}|\boldsymbol{z})] \end{aligned} \] 其中，第一项就指的是我们假设的后验分布\(q(\boldsymbol{z}|\boldsymbol{x})\)和先验分布\(p(\boldsymbol{z})\)尽量接近，而第二项则代表不断在\(\boldsymbol{z}\)上采样，然后使得被重构的样本中重构\(\boldsymbol{x}\)的概率最大。而其实第二项也可以看成是重建误差，这是因为解码器为一个固定结构，因此从\(\boldsymbol{z}\)到\(\hat{\boldsymbol{x}}\)的转换也是固定的，也就是说\(\log p(\boldsymbol{x}|\boldsymbol{z})\)其实等价于\(\log p(\boldsymbol{x}|\hat{\boldsymbol{x}})\)。

在实际中，我们通常使用高斯分布去构造VAE，即\(p\)和\(q\)满足高斯分布，而\(p(\boldsymbol{z})\)为标准的正态分布。此时，损失函数可以写为： \[ L=\frac{1}{2}\sum_{j=1}^{J}(1+\log \sigma_j^2 -\mu_j^2-\sigma_j^2)+||\boldsymbol{x}-\hat{\boldsymbol{x}}||_2 \]

代码示例

下面为使用变分自编码器来生成动漫头像的示例代码，其中一些部分从https://github.com/AntixK/PyTorch-VAE/blob/master/models/vanilla_vae.py和https://github.com/wuga214/IMPLEMENTATION_Variational-Auto-Encoder改编而来。使用的数据集可以从Anime-Face-Dataset数据集介绍 | 文艺数学君 (mathpretty.com)下载而得。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
from torch.optim import Adam, RMSprop
from torch.utils.data import DataLoader, Dataset
import os
import cv2
import numpy as np
from PIL import Image
from torchvision.datasets import ImageFolder
import matplotlib.pyplot as plt

dataset = ImageFolder(root='./generate/', transform=torchvision.transforms.Compose([ #root='./generate/'
    torchvision.transforms.Resize(64),
    torchvision.transforms.CenterCrop(64),
    torchvision.transforms.ToTensor(),
    torchvision.transforms.Normalize((0.5, 0.5, 0.5),(0.5, 0.5, 0.5)),
]))
dataloader = DataLoader(dataset, batch_size=128)

class VAE(nn.Module):
    # 网络结构的影响：在使用ReLU激活函数时，效果很差，换成LeakyReLU之后好很多。原因可能与ReLU将0以下的值全部抑制掉有关
    def __init__(self, observation_std=0.01): #此处的observation_std个人理解相当于是为重建误差加上不同的权重
        super(VAE, self).__init__()
        self.Observation_std = torch.tensor(observation_std)
        #我们将输入设为3*128*128的图片
        self.Encode=nn.Sequential(
            nn.Conv2d(3,64,4,2,1,bias=False), #输出为64*32*32
            nn.LeakyReLU(inplace=True),
            nn.Conv2d(64,128,4,2,1,bias=False), #输出为128*16*16
            nn.BatchNorm2d(128),
            nn.LeakyReLU(inplace=True),
            nn.Conv2d(128,256,4,2,1,bias=False), #输出为256*8*8
            nn.BatchNorm2d(256),
            nn.LeakyReLU(inplace=True), 
            nn.Conv2d(256,512,4,2,1,bias=False), #输出为512*4*4
            nn.LeakyReLU(inplace=True),
            nn.BatchNorm2d(512),
            nn.Conv2d(512,512,4,1,0,bias=False), #输出为512*1*1
        )
        
        self.EncodeMean=nn.Linear(512,1024)
        self.EncodeLogvar=nn.Linear(512,1024) #由于标准差的值是正数，而我们无法保证全连接层的输出全部为正，因此将此处的输出认为是标准差求对数之后的结果
        
        #此处的输入为1024*1*1
        self.Decoder=nn.Sequential(
            nn.ConvTranspose2d(1024,512,4,1,0,bias=False), #512*4*4
            nn.BatchNorm2d(512),
            nn.LeakyReLU(inplace=True),
            nn.ConvTranspose2d(512,256,4,2,1,bias=False), #256*8*8
            nn.BatchNorm2d(256),
            nn.LeakyReLU(inplace=True),
            nn.ConvTranspose2d(256,128,4,2,1,bias=False), #128*16*16
            nn.BatchNorm2d(128),
            nn.LeakyReLU(inplace=True),
            nn.ConvTranspose2d(128,64,4,2,1,bias=False), #64*32*32
            nn.BatchNorm2d(64),
            nn.LeakyReLU(inplace=True),        
            nn.ConvTranspose2d(64,3,4,2,1,bias=False), #3*64*64
            nn.Tanh()
        )
    
    def encode(self,x):
        x=self.Encode(x)
        x=x.reshape((-1, 512))
        mean=self.EncodeMean(x)
        logvar=self.EncodeLogvar(x)
        return mean, torch.exp(logvar)
    
    def reparameterize(self, mean, var):
        epsilon=torch.randn_like(mean)
        std=torch.sqrt(var)
        res=torch.add(torch.mul(epsilon,std),mean)
        return res
    
    def decode(self,x):
        x=x.reshape((-1,1024,1,1))
        x=self.Decoder(x)
        observation_epsilon=torch.randn_like(x)
        return x+observation_epsilon*self.Observation_std
    
    def forward(self,x):
        mean,var=self.encode(x)
        sample=self.reparameterize(mean,var)
        return self.decode(sample), mean, var

# 经过试验，学习率不能太高，使用2e-6的学习率就会出现梯度爆炸的情况。而且经测试，Adam优化器的训练效果也不如RMSprop
LearningRate=1e-6
Device='cuda' if torch.cuda.is_available() else 'cpu'
Observation_std=0.01

model=VAE(observation_std=Observation_std)
model.to(Device)
optimizer=RMSprop(model.parameters(),lr=LearningRate) 
#optimizer=Adam(model.parameters(),lr=LearningRate)

def show_and_save_figure(fig_array, show_figure=False, save_figure=False, save_path='./output_vae/', save_figurename=None):
    plt.figure(figsize=(15,15))
    plt.subplot(1,1,1)
    plt.axis('off')
    plt.imshow(np.transpose(fig_array.cpu(), (1,2,0)))
    if show_figure:
        plt.show()
    if save_figure:
        plt.savefig(save_path+save_figurename)
    plt.close()

1 2	fixed_noise=torch.randn((64, 1024), device=Device) img_list=[]

for i in range(100):
    model.train()
    error=0.0
    for data, _ in dataloader:
        data=data.to(Device)
        reconstruct, mean, var=model(data)
        reconstruct_loss=0.5*torch.mean((data-reconstruct)*(data-reconstruct)/(2*model.Observation_std*model.Observation_std)) + torch.log(model.Observation_std)
        KLD_loss=torch.mean(-1/2*(1.0+torch.log(var+1e-8)-mean*mean-var))
        loss=reconstruct_loss+KLD_loss
        loss.backward()
        optimizer.step()
        error+=loss.detach().cpu()*128
        torch.save(model, 'model.pt')
    print('epoch: ',i,', loss:',error)
    with torch.no_grad():
        fake=model.decode(fixed_noise).detach().cpu()
    img_list.append((torchvision.utils.make_grid(fake,padding=2,normalize=True)))
    show_and_save_figure(img_list[-1], save_figure=True, save_figurename=str(i)+'.jpg')

在训练100轮之后，生成的图像如下：

我们可以看到，在训练100轮之后，VAE只能生成看起来模糊的动漫头像。而且在实际的调参过程中发现，训练VAE时使用的学习率比较难调整，稍微高一点便会随着训练的进行出现梯度爆炸的现象。

参考

深度学习，GoodFellow
自编码器AutoEncoder，降噪自编码器DAE，稀疏自编码器SAE，变分自编码器VAE 简介 - Jerry_Jin - 博客园 (cnblogs.com)
降噪自动编码器（Denoising Autoencoder) - Physcal - 博客园 (cnblogs.com)
www.iro.umontreal.ca/~lisa/publications2/index.php/attachments/single/176
AutoEncoder: 稀疏自动编码器 Sparse_AutoEncoder - 知乎 (zhihu.com)
如何通俗的解释交叉熵与相对熵？ - 知乎 (zhihu.com)
半小时理解变分自编码器 - 知乎 (zhihu.com)
变分自编码器VAE：原来是这么一回事 | 附开源代码 - 知乎 (zhihu.com)
https://arxiv.org/pdf/1312.6114v10.pdf

Yufei Luo's Blog

深度学习-自编码器

概述