"> "> 机器学习-K近邻算法 | Yufei Luo's Blog

Yufei Luo's Blog

But I was so much older then, I am younger than that now.

Yufei Luo's Blog

机器学习-K近邻算法

发表于 更新于 分类于 ， 阅读次数：
本文字数： 4.9k 阅读时长 ≈ 4 分钟

概述

K近邻（K-Nearest Neighbors）算法是一种基本的回归与分类算法。它的工作原理是，给定一个测试样本，然后基于与这个测试样本最近的\(k\)个“邻居”的信息来进行预测。对于回归任务来说，通常使用投票法，选择\(k\)个样本中出现最多的类别标记作为预测结果；在回归任务中使用平均法，将\(k\)个样本结果的平均作为预测结果。此外，对于这\(k\)个样本还可以基于距离或者其它权重来进行加权。

原理

特征空间分割

K近邻法使用的模型实质上对应于特征空间的划分。以分类问题为例，当训练集、距离度量方式、K值以及分类决策规则确定后，对于任何一个新的输入实例，它所属的类便被唯一地确定。这相当于是根据这些要素将特征空间划分为不同的子空间，每个子空间内的点属于某一个类。

下图是使用K近邻分类时，对二维空间划分的一个例子：

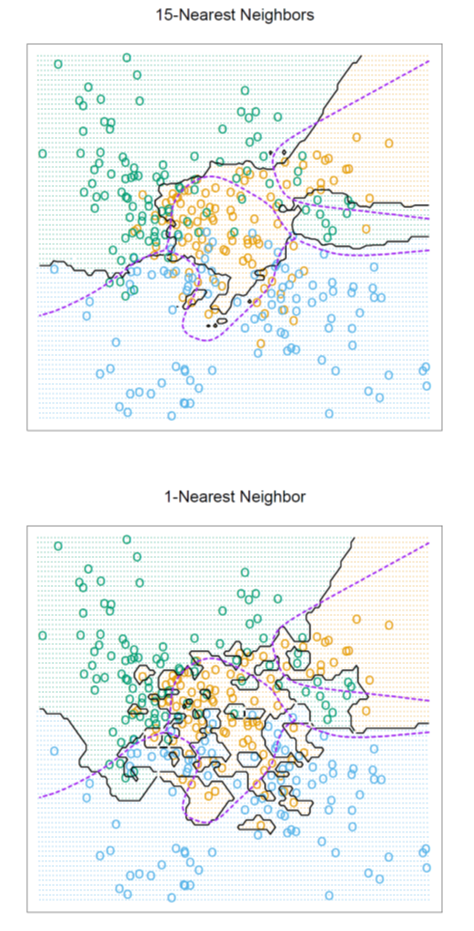
image-20210310230111610

距离度量

K近邻算法中，距离度量对于算法的结果也有着很大影响，使用不同的距离计算公式可能会使确定的近邻点也不同。K近邻中的距离计算与聚类算法中的距离计算可采用同样的方法，可进一步阅读本博客内介绍聚类的博文，其中包含距离计算的相关内容。

K值的选择

K值的选择会对结果造成很大影响。如果K值选择的过小，那么预测结果会对近邻的数据点十分敏感，容易受到噪声或者离群点的干扰，这样意味着模型会变得复杂，因此会容易过拟合；

如果K值选择的过大，就相当于是用一个较大邻域内的训练实例进行预测，此时相当于是模型较为简单，容易欠拟合。对于模型变简单的解释，我们考虑最极端的情况，取K=N（N为训练样本的数目），那么此时无论输入是什么，其输出都不会变化。

在实际中，通常使用交叉验证法选择K的值。

实现：kd树

在实现K近邻法时，影响算法速度的主要因素便是如果快速地搜索出K个近邻点。最简单的实现方式是线性扫描，但是这种方式需要计算每一个训练样本与待预测样本的距离。当训练集很大时，这种方法显然不可取。为了提高K近邻的搜索效率，可以使用kd树的数据结构来保存训练集。

kd树是一种对K维空间中的实例点进行存储以便对其进行快速检索的树形数据结构，属于二叉树的一种。构造kd树的过程相当于不断地用垂直于坐标轴的超平面将K维空间切分，构成一系列的K维超矩形区域，kd树的每一个结点便对应于一个超矩形区域。

给定一个K维空间的数据集\(D=\{\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_m\}\)，其中\(\boldsymbol{x}_i=(x_{i1},x_{i2},\dots,x_{in})\)，\(D\)对应的kd树可以采用如下的步骤进行构造：

  1. 构造根结点，根结点对应于包含\(D\)的K维超矩形区域
  2. 在深度为\(j\)的结点处，选择\(x^{(l)}\)作为切分的坐标轴，其中\(l=j~(\text{mod}~k) +1\)，以该结点所对应区域中所有样本的\(x^{(l)}\)坐标的中位数作为切分点，将该结点对应的超矩形区域切分为两个区域。切分的方式是通过构造一个通过切分点并且与坐标轴\(x^{(l)}\)垂直的超平面实现。
  3. 基于上一步得到的结点，生成深度为\(j+1\)的左、右子结点，左子结点对应于坐标\(x^{(l)}\)小于切分点的子区域，右子结点对应于坐标\(x^{(l)}\)大于切分点的子区域。将落在切分超平面上的样本保存在该结点处。
  4. 重复步骤2和3，直到两个子区域只有一个实例存在。这样便形成了kd树的区域划分。

以二维平面为例，一棵kd树及其对应的特征空间划分如下图所示：

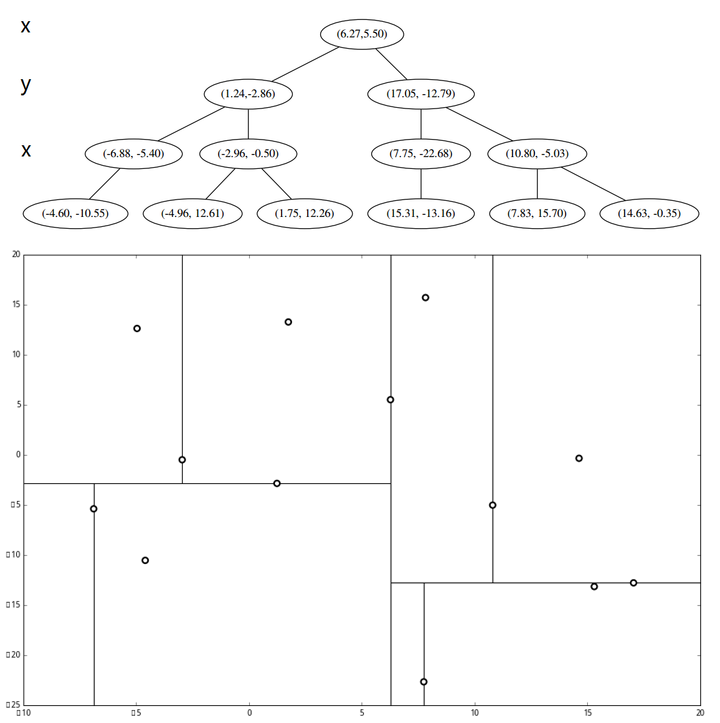
image-20210311225317771

基于kd树，搜索点\(p\)的最近邻点可以按照如下步骤：

  1. 根据\(p\)的坐标值和kd树中每个结点的切分一直向下搜索，如果当前维度的坐标小于切分点坐标则向左子树移动，反之向右子树移动，直至到达一个叶结点
  2. 以此叶结点为最近点，递归地向上回溯。在回溯的过程中，会遇到两种情况：
    1. 某个结点保存的样本点比当前最近点距离目标点更近，则以该样本点作为当前最近点。
    2. 由于当前最近点一定属于该结点的其中一个子结点对应的区域，因此需要检查这一子结点的兄弟结点中是否存在更近的点。这可以通过做一个以\(p\)点为球心，以\(p\)与当前最近点之间距离为半径的超球体，并检查兄弟结点对应的区域是否与这个超球体相交。如果相交则需要检查兄弟结点对于的区域内是否存在更近的点；否则往上一层继续回退。
  3. 重复步骤2，直至回退到根结点处。最后的当前最近点就是\(p\)的最近邻点。

对于kd树来说，其最坏情况下的搜索时间会退化为线性（如果样本的分布比较特殊）；但是当样本随机分布时，其平均时间复杂度为\(O(\log N)\)。而且如果训练集的样本数接近于小于样本的特征数时，其效率会迅速下降，接近线性扫描。

优缺点

优点：

  1. 简单，易于理解，易于实现，无需估计参数；
  2. 训练时间为零。它没有显式的训练，KNN只是把样本保存起来，收到测试数据时再处理，所以KNN训练时间为零；
  3. 适用于回归以及分类问题，而且天然可以处理多分类问题，适合对稀有事件进行分类；
  4. 对数据没有假设，准确度高，对异常点不敏感。

缺点：

  1. 计算量较大，尤其是数据特征数目较多时；
  2. 可理解性较差，无法给出类似于决策树那样的规则；
  3. 属于懒惰学习方法，因此预测时速度比起逻辑回归之类的算法慢；
  4. 样本不平衡的时候，对稀有类别的预测准确率低；
  5. 对训练数据依赖度大，因此对训练数据的容错性较差。

代码示例

分类

我们使用Sklearn自带的Iris数据集，来演示如何用sklearn中的KNN分类器KNeighborsClassifier做分类任务。

Iris数据集的四个特征分别为：sepal length (cm)、sepal width (cm)、petal length (cm)、petal width (cm)，三种不同的类别0、1、2分别对应于Iris-Setosa、Iris-Versicolour和Iris-Virginica这三类。

为了方便做可视化，我们对数据进行精简，只选取2、3两列来训练与预测模型。我们取petal length (cm)和petal width (cm)这两个特征来训练和预测。

1
2
3
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
1
2
3
4
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix
1
2
3
X,y=load_iris(return_X_y=True)
X=X[:,2:4]
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3)

模型比较重要的参数：

  • n_neighbors: 根据多少个邻居的信息做判断，默认为5
  • weight：每个邻居的权重，默认为uniform，即每个邻居权重相等；另一种参数是distance，即按照距离来赋予权重；也可以自己传入函数
  • metric：计算距离的方法，默认为闵氏距离，也可以使用其它方法，或是传入自定义函数
  • p：在使用闵氏距离时，公式中的指数等于几，默认为2（即欧式距离）
1
clf=KNeighborsClassifier()
1
2
3
X_mesh,Y_mesh=np.meshgrid(np.linspace(0,8,200),np.linspace(0,5,100))
XY_mesh=np.concatenate([X_mesh.reshape(-1,1),Y_mesh.reshape(-1,1)],axis=1)
mesh=clf.predict(XY_mesh)

我们分别取K=1、4、7，来比较KNN分类器在使用不同的K值训练之后所得到的分类边界。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
fig=plt.figure(figsize=(15,3))
axes=fig.subplots(1,3)
for i in range(3):
    clf=KNeighborsClassifier(n_neighbors=i*3+1)
    clf.fit(train_x,train_y)
    pred_y=clf.predict(test_x)
    mesh=clf.predict(XY_mesh)
    axes[i].set_title('Neighbor={}'.format(i*3+1))
    axes[i].set_xlabel('sepal length (cm)')
    axes[i].set_ylabel('sepal width (cm)')
    contour=axes[i].contourf(X_mesh,Y_mesh,mesh.reshape(X_mesh.shape),cmap='Greys')
    fig.colorbar(contour,ax=axes[i])
    axes[i].scatter(test_x[test_y==0][:,0],test_x[test_y==0][:,1],label='Iris-Setosa')
    axes[i].scatter(test_x[test_y==1][:,0],test_x[test_y==1][:,1],label='Iris-Versicolour')
    axes[i].scatter(test_x[test_y==2][:,0],test_x[test_y==2][:,1],label='Iris-Virginica')
    axes[i].legend()
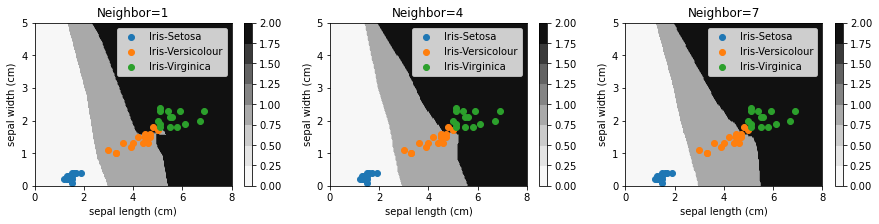
KNN分类

从上图中可以看出，随着K值的增大，分类边界逐渐变得平滑。

回归

我们使用Sklearn自带的Diabetes数据集，来演示如何用sklearn中的KNN做回归任务。这一数据集共有10个特征，且这些特征都已经被标准化至\((-2,2)\)区间内，待预测的值是25-346范围内的整数。由于我们的目的主要是说明模型的用法，因此省略了特征工程的步骤，将这些数据直接用来训练模型。

1
2
3
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
1
2
X,y=load_diabetes(return_X_y=True)
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3)

KNeighborsRegressor回归器的重要参数与KNeighborsClassifier分类器的参数相同，故此处不再赘述。

1
2
3
4
reg=KNeighborsRegressor(n_neighbors=10,weights='distance')
reg.fit(train_x,train_y)
pred=reg.predict(test_x)
errors=pred-test_y

参考

  1. 机器学习，周志华
  2. 统计学习方法，李航
  3. https://zhuanlan.zhihu.com/p/23966698
  4. https://zhuanlan.zhihu.com/p/26029567
  5. https://zhuanlan.zhihu.com/p/25994179
  6. https://blog.csdn.net/v_july_v/article/details/8203674
  7. https://www.cnblogs.com/lsm-boke/p/11756173.html