"> "> 机器学习-高斯过程回归 | Yufei Luo's Blog

Yufei Luo's Blog

But I was so much older then, I am younger than that now.

Yufei Luo's Blog

机器学习-高斯过程回归

发表于 更新于 分类于 ， 阅读次数：
本文字数： 5.6k 阅读时长 ≈ 5 分钟

高斯过程

在概率论和统计学中，高斯过程指的是观测值出现在一个连续输入空间（如时间或空间）的随机过程。在高斯过程中，连续输入空间中的每个点都是与一个正态分布的随机变量相关联；此外，这些随机变量组成的有限集合也都对应于一个多元正态分布。

用数学语言可以描述为：假设有一组随机变量\(\{\xi_t\},t\in T\)，\(T\)代表一个连续域，如果对于\(\forall n\in N^+\)，都有\(t_1,t_2,\dots,t_n \in T\)，并且满足\(\xi_{t_1},\xi_{t_2},\dots,\xi_{t_n}\triangleq \xi_{t_1 \sim t_n }\sim \mathcal{N}(\mu_{t_1 \sim t_n },\Sigma_{t_1 \sim t_n })\)，那么我们就称\(\{\xi_t\},t\in T\)是一个高斯过程\(\mathcal{GP}(\mu,\sigma^2)\)。通俗地讲，也就是说有一系列在时间或者空间上连续的点\(\{\xi_t\}\)，如果按照时间或者空间分开看的话每个\(\{\xi_t\}\)各自符合一个一维的高斯分布，而它们合起来看则是符合一个多维的高斯分布。

一个高斯过程可以被它的均值函数和协方差函数所定义，即： \[ f(\boldsymbol{x}) \sim \mathcal{GP}(m(\boldsymbol{x}),k(\boldsymbol{x},\boldsymbol{x'})) \] 其中， \[ m(\boldsymbol{x})=E[f(\boldsymbol{x})] \\ k(\boldsymbol{x},\boldsymbol{x}')=E[(f(\boldsymbol{x})-m(\boldsymbol{x}))(f(\boldsymbol{x}')-m(\boldsymbol{x}'))] \] 也就是说，高斯过程相当于是函数的一种概率分布。\(k\)为核函数，可以使用任意一种如线性核、高斯核等。而核函数也决定了高斯过程的性质。

下图所示为一个确定的高斯过程（均值为0，核函数的参数也固定）产生的一系列函数曲线：

img

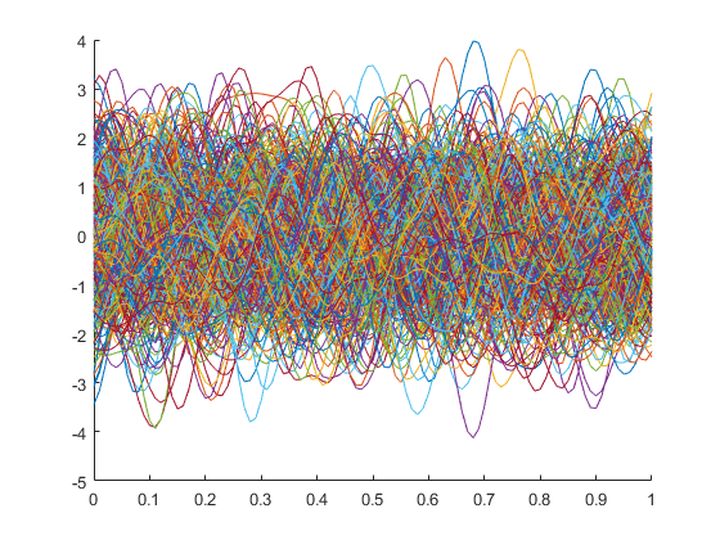
从中可以看到很多杂乱的曲线，但是它们具有一些规律，就是多数函数值都在-2~2之间波动。如果我们在上图中的某一个固定的\(x\)值处采样，可得如下的统计结果。可以明显看到，采样得到的这些函数值满足高斯分布：

img

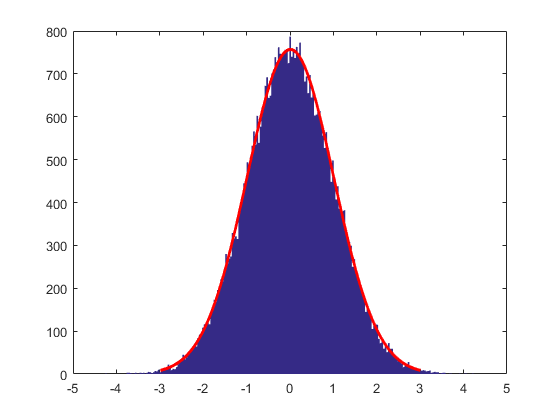
也就是说，连续输入空间（时间或者是空间）中每个点都是与一个高斯分布的随机变量相关联（相当于是在我们观测的时候，这些点“巧合”地出现在了观测点处）。即，在任意一个时间或者空间点上，对应的随机变量都是满足高斯分布，而这个被满足的高斯分布的参数（mean和variance）又是被对应的高斯过程的中的mean function和covariance function所确定的。

备注：随机过程的概念

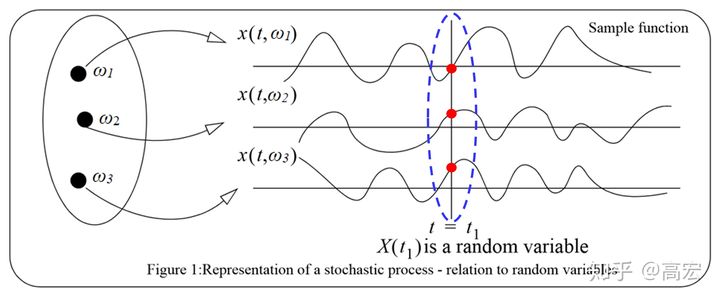
随机过程是定义在\(\Omega \times T\)上的二元函数\(X(\omega,t)\)，其中\(\Omega\)代表样本空间，\(T\)代表一个连续域（如时间或者空间）。对于固定的\(t\)，\(X(\omega,t)\)为随机变量，记作\(X(t)\)或\(X_t\)（它不是\(t\)的函数，只表示所有样本函数在\(t\)处的取值）；而对于固定的\(\omega\)，\(X(\omega,t)\)为\(t\)的一般函数，称为样本函数或者样本轨道，记为\(x(t)\)。它们的概念可以表示为下图：

img

在介绍完高斯过程的定义之后，下面我们对高斯过程回归的算法原理进行推导。

算法原理

我们考虑一个带有噪声的回归模型\(y=f(\boldsymbol{x})+\epsilon\)，其中\(f(\boldsymbol{x})\)来自于一个参数待定的高斯过程\(f(\boldsymbol{x})\sim \mathcal{GP}(\mu,k)\)，噪声满足\(\epsilon \sim \mathcal{N}(0,\sigma_n^2)\)。给定一系列多维的观测点\(D=\{\boldsymbol{x}_i,y_i\},\boldsymbol{x}_i \in \R^p,y_i \in \R,i=1,2,\dots,n\)，我们假定样本是来自于一个参数待定的确定形式高斯过程的一个样本（即对应于无数多条样本曲线中的一条）。按照高斯过程的定义，这些点的联合分布\([f(\boldsymbol{x}_1),f(\boldsymbol{x}_2),\dots,f(\boldsymbol{x}_n)]\)需要满足一个多维的高斯分布 \[ [f(\boldsymbol{x}_1),f(\boldsymbol{x}_2),\dots,f(\boldsymbol{x}_n)] \sim \mathcal{N}(\boldsymbol{\mu},K) \] 其中\(\boldsymbol{\mu}=[\mu(\boldsymbol{x}_1),\mu(\boldsymbol{x}_2),\dots,\mu(\boldsymbol{x}_n)]\)为均值向量；\(K\)是一个\(n\times n\)的矩阵，其中第\((i,j)\)个元素\(K_{ij}=k(\boldsymbol{x}_i,\boldsymbol{x}_j)\)。

为了去预测未知数据\(f^*=f(Z),Z=[\boldsymbol{z}_1,\boldsymbol{z}_2,\dots,\boldsymbol{z}_m]^T\)。考虑到高斯分布的性质，我们可以得到训练点和预测点的联合分布为： \[ \begin{bmatrix} \boldsymbol{y} \\ f^* \end{bmatrix} = \mathcal{N} \left( \begin{bmatrix} \boldsymbol{\mu}(X) \\ \boldsymbol{\mu}(Z) \\ \end{bmatrix}, \begin{bmatrix} K(X,X)+\sigma_n^2I & K(Z,X)^T \\ K(Z,X) & K(Z,Z) \end{bmatrix} \right) \] 其中\(\boldsymbol{\mu}(X)=\boldsymbol{\mu}\)，\(\boldsymbol{\mu}(Z)=[\mu(\boldsymbol{z}_1),\mu(\boldsymbol{z}_2),\dots,\mu(\boldsymbol{z}_m)]^T\)；\(K(X,X)=K\)；\(K(Z,X)\)是一个\(m\times n\)的矩阵，其中第\((i,j)\)个元素\([K(Z,X)]_{ij}=k(\boldsymbol{z}_i,\boldsymbol{x}_j)\)；\(K(Z,Z)\)是一个\(m\times m\)的矩阵，其中其中第\((i,j)\)个元素\([K(Z,Z)]_{ij}=k(\boldsymbol{z}_i,\boldsymbol{z}_j)\)

利用高斯分布的条件分布性质（推导过程略复杂，故此处不再详细解释，可参考https://blog.csdn.net/qq_37394299/article/details/103071404），我们可以得到： \[ p(f^*|X,\boldsymbol{y},Z)=\mathcal{N}(\hat{\boldsymbol{\mu}},\hat{\Sigma}) \] 其中， \[ \hat{\boldsymbol{\mu}}=K(X,Z)^T(K(X,X)+\sigma_n^2I)^{-1}(\boldsymbol{y}-\boldsymbol{\mu}(X))+\boldsymbol{\mu}(Z) \\ \hat{\Sigma}=K(Z,Z)-K(X,Z)^T(K(X,X)+\sigma_n^2I)^{-1}K(X,Z) \] 从\(\hat{\boldsymbol{\mu}}\)的表达式中也可以看出，\(\hat{\boldsymbol{\mu}}\)中的每一个元素\(\hat\mu^*\in \hat{\boldsymbol{\mu}}\)可以写作\(\hat{\mu}^*=\sum_{i=1}^{N}\alpha_ik(\boldsymbol{x}_i,\boldsymbol{x}_*)\)，相当于是核函数\(k\)的线性组合。而这一表达式的形式与加了核函数的岭回归类似。也就是从高斯过程回归的角度考虑的话，核岭回归其实一定程度上等价于高斯过程回归。

下图为一维数据使用高斯过程回归得到的结果：

img

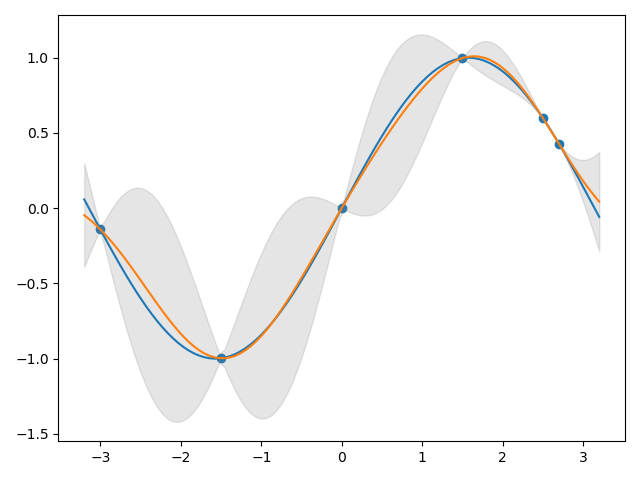
如果数据不满足高斯分布，也是可以使用高斯过程回归进行拟合的。原因在于，高斯过程是高斯分布的无限维拓展，因而任意有限个点必然可以视作任意一个高斯过程的一个随机抽样。当然这样的结论不仅仅是对于高斯过程，对于任何其他随机过程都是成立的。那么给定一组数据，无论是否服从高斯分布，它们都可以视作任意一个高斯过程的一个随机抽样，因此对其回归建模从理论上讲可以考虑高斯过程回归。

优缺点

优点：

  1. 预测值是训练数据集的插值，可以不需要计算显式的函数表达式；
  2. 预测值是概率的，可以据此计算置信区间，然后根据这些区域选出某个感兴趣的区域做进一步的分析；
  3. 可以使用不同的核函数。

缺点：

  1. 无法处理缺失值；
  2. 当特征数目较多时，在高维空间会失去有效性。

代码示例

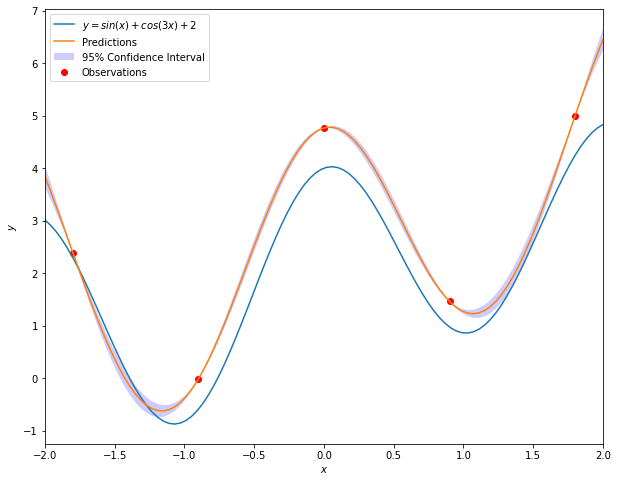
接下来我们使用带有噪声的伪造数据来演示高斯过程回归的使用方法。具体地，用于训练模型的数据集产生自函数\(y=sin(x)+cos(3x)+2+\epsilon\)。然后我们将模型预测值与这一函数表达式对应的真实值进行对比，并绘制出模型给出的95%置信区间。

1
2
3
4
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib
1
from sklearn.gaussian_process import GaussianProcessRegressor
1
2
3
4
x_pred=np.linspace(-2,2,100).reshape(-1,1)
y_truth=np.sin(x_pred)+2*np.cos(3*x_pred)+2
x_train=np.linspace(-1.8,1.8,5).reshape(-1,1)
y_noise=np.sin(x_train)+2*np.cos(3*x_train)+2+np.random.rand(*x_train.shape)
1
2
3
4
reg=GaussianProcessRegressor()
reg.fit(x_train,y_noise)
y_pred,sigma=reg.predict(x_pred,return_std=True)
sigma=sigma.reshape(-1,1)
1
2
3
4
5
6
7
8
9
10
fig=plt.figure(figsize=(10,8))
axes=fig.subplots(1,1)
axes.plot(x_pred,y_truth,label='$y=sin(x)+cos(3x)+2$')
axes.plot(x_pred,y_pred,label='Predictions')
axes.fill(np.concatenate([x_pred,x_pred[::-1]]),np.concatenate([y_pred-1.9600*sigma,(y_pred+1.9600*sigma)[::-1]]),alpha=0.2,fc='b',ec='None',label='95% Confidence Interval') #标准正态分布下，[-1.96,1.96]区间内的面积为0.95
axes.scatter(x_train,y_noise,label='Observations',c='r')
axes.set_xlim(-2,2)
axes.set_xlabel('$x$')
axes.set_ylabel('$y$')
axes.legend()
高斯过程回归-代码示例

参考

  1. Machine Learning: A Probabilistic Perspective
  2. Gaussian Process for Machine Learning
  3. 什么是Gaussian process? —— 说说高斯过程与高斯分布的关系 - 知乎 (zhihu.com)
  4. 如何从深刻地理解随机过程的含义？ - 知乎 (zhihu.com)
  5. [机器学习基础 11]白板推导 高斯过程 - 知乎 (zhihu.com)
  6. Gaussian process regression的简洁推导——从Function-space角度看 - 知乎 (zhihu.com)
  7. 浅谈高斯过程回归 - 知乎 (zhihu.com)
  8. 【答疑解惑-II】——不满足正态分布的数据到底能不能用Gaussian process的方法呢？ - 知乎 (zhihu.com)
  9. 【答疑解惑-I】——Gaussian process的样本生成与其mean和kernel的联系 - 知乎 (zhihu.com)
  10. GitHub - jwangjie/Gaussian-Processes-Regression-Tutorial: An Intuitive Tutorial to Gaussian Processes Regression