"> "> 机器学习-朴素贝叶斯 | Yufei Luo's Blog

Yufei Luo's Blog

But I was so much older then, I am younger than that now.

Yufei Luo's Blog

机器学习-朴素贝叶斯

发表于 更新于 分类于 ， 阅读次数：
本文字数： 5.3k 阅读时长 ≈ 5 分钟

算法原理

朴素贝叶斯算法是基于贝叶斯定理和特征条件独立假设的分类方法。对于给定的训练数据集，算法会基于特征条件独立假设学习输入和输出的联合概率分布；然后对于给定的输入，利用贝叶斯定理求出后验概率最大的输出。这种算法实现简单，学习与预测效率都较高。

使用数学语言，朴素贝叶斯算法可以描述如下：

设输入空间\(\mathcal{X}\subseteq R^n\)为\(n\)维向量的集合，输出空间为类标记集合\(\mathcal{Y}=\{c_1,c_2,\dots,c_K\}\)。输入为特征向量\(\boldsymbol{x}\in \mathcal{X}\)，输出为类标记\(y\in \mathcal{Y}\)。\(X\)是定义在输入空间\(\mathcal{X}\)上的随机向量，\(Y\)是定义在输出空间\(\mathcal{Y}\)上的随机变量。\(P(X,Y)\)是\(X\)和\(Y\)的联合概率分布，训练数据集\(D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),\dots,(\boldsymbol{x}_m,y_m)\}\)由\(P(X,Y)\)独立同分布产生。朴素贝叶斯法通过训练数据集学习联合概率分布\(P(X,Y)\)。具体来说，联合概率分布\(P(X,Y)\)是通过计算先验概率分布\(P(Y=c_k),k=1,2,\dots,K\)与条件概率分布\(P(X=\boldsymbol{x}|Y=c_k)=P(X^{(1)}=x^{(1)},\dots,X^{(n)}=x^{(n)}|Y=c_k),k=1,2,\dots,K\)来计算的。

但是，如果考虑每个特征之间两两关联的话，条件概率分布的估计将会十分困难，可能会涉及到指数级数量的参数。因此，朴素贝叶斯算法做了一个较强的假设，即假设每个特征之间两两独立，互不相关，这也被称为条件独立性假设（如果特征之间非独立，则变为贝叶斯网络）。条件独立性假设可以表示如下： \[ \begin{aligned} P(X=\boldsymbol{x}|Y=c_k)=&P(X^{(1)}=x^{(1)},\dots,X^{(n)}=x^{(n)}|Y=c_k) \\ =&\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k) \end{aligned} \] 朴素贝叶斯法在分类时，对于给定的输入\(\boldsymbol{x}\in \mathcal{X}\)，通过学习到的模型计算后验概率分布\(P(Y=c_k|X=\boldsymbol{x})\)，将后验概率最大的类作为\(\boldsymbol{x}\)的分类。后验概率的计算通过贝叶斯定理进行： \[ P(Y=c_k|X=\boldsymbol{x})=\frac{P(X=\boldsymbol{x}|Y=c_k)P(Y=c_k)}{\sum_k P(X=\boldsymbol{x}|Y=c_k)P(Y=c_k)} \] 根据条件独立性假设，上述公式变为： \[ P(Y=c_k|X=\boldsymbol{x})=\frac{P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}|Y=c_k)} \] 因此，朴素贝叶斯分类器可以表示为： \[ y=f(\boldsymbol{x})=\text{arg}\max_{c_k} \frac{P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}|Y=c_k)} \] 其中，对于所有分母来说\(c_k\)都是相同的，因此可以简化为： \[ y=\text{arg}\max_{c_k} P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}|Y=c_k) \] 朴素贝叶斯法在将实例分到后验概率最大的类中，其实等价于期望风险最小化。假设我们选择0-1损失函数： \[ L(Y,f(X))= \begin{cases} 1,Y\ne f(X) \\ 0,Y=f(X) \end{cases} \] 其中\(f(X)\)代表分类决策函数。

此时，我们可以计算出关于\(X\)的条件期望风险： \[ \begin{aligned} R_{exp}(f)=&E[L(Y,f(X))] \\ =&E_{X}\sum_{k=1}^{K} [L(c_k,f(X))]P(c_k|X) \end{aligned} \] 为了使得期望风险最小化，只需要对\(X=\boldsymbol{x}\)逐个极小化，由此可得： \[ \begin{aligned} f(\boldsymbol{x})=&\text{arg}\min_{y\in \mathcal{Y}} \sum_{k=1}^{K}L(c_k,y)P(c_k|X=\boldsymbol{x}) \\ =&\text{arg}\min_{y\in \mathcal{Y}} \sum_{k=1}^{K}P(y\ne c_k|X=\boldsymbol{x}) \\ =&\text{arg}\min_{y\in \mathcal{Y}} (1-P(y=c_k|X=\boldsymbol{x})) \\ =&\text{arg}\max_{y\in \mathcal{Y}} P(y=c_k|X=\boldsymbol{x}) \end{aligned} \] 因此，期望风险最小化就等价于是后验概率最大化。

参数估计

在朴素贝叶斯算法中，我们需要估计先验概率\(P(Y=c_k)\)与条件概率分布\(P(X^{(j)}=x^{(j)}|Y=c_k)\)的值。可以使用极大似然估计法去估计相应的概率值。

先验概率\(P(Y=c_k)\)的极大似然估计是： \[ P(Y=c_k)=\frac{\sum_{i=1}^{N} I(y_i=c_k)}{N} \] 我们设第\(j\)个特征\(x^{(j)}\)可能取值的集合为\(\{a_{j1},a_{j2},\dots,a_{jS_j}\}\)，条件概率\(P(X^{(j)}=a_{jl}|Y=c_k)\)的极大似然估计为： \[ P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^{N} I(x_i^{(j)}=a_{jl},y_i=c_k)}{\sum_{i=1}^{N} I(y_i=c_k)} \] 其中，\(x_i^{(j)}\)代表第\(i\)个样本的第\(j\)个特征；\(a_{jl}\)是第\(j\)个特征可能取的第\(l\)个值；\(I\)为指示函数，代表条件成立时的值为1，反之为0。\(j=1,2,\dots,n~;~l=1,2,\dots,S_j~;~k=1,2,\dots,K\)。

注：在实际使用中，可能会遇到一些数值型的特征。对于这种特征，需要将其转换为类别型的特征。例如可以通过分段的方式，根据数据落在哪个分段，将其归入相应的类别中去。

需要注意到的是，用极大似然估计可能会出现要估计的概率值为0的情况，因为当某个数据中\(P(X^{(j)}=a_{jl}|Y=c_k)\)的值为0时，则会使得后验概率分布\(P(Y=c_k|X=\boldsymbol{x})\)的值为0。解决这一问题的办法是采用贝叶斯估计，即条件概率\(P(X^{(j)}=a_{jl}|Y=c_k)\)使用如下的表达式进行计算： \[ P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^{N} I(x_i^{(j)}=a_{jl},y_i=c_k)+\lambda}{\sum_{i=1}^{N} I(y_i=c_k)+S_j \lambda} \] 其中\(\lambda \ge 0\)。当\(\lambda=0\)时，它与极大似然估计等价；而当\(\lambda >0\)时，等价于在随机变量各个取值的频数上赋予一个正数\(\lambda\)（注意这样仍然是一个概率分布）。

优缺点

优点：

  1. 对小规模的数据表现很好；
  2. 能处理多分类任务；
  3. 对缺失数据不太敏感；
  4. 算法也比较简单。

缺点：

  1. 朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好；

  2. 需要知道先验概率，且先验概率很多时候取决于假设，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

  3. 对输入数据的表达形式很敏感。

代码示例

我们使用Sklearn自带的Iris数据集，来演示如何用sklearn中的朴素贝叶斯分类器做分类任务。

Iris数据集的四个特征分别为：sepal length (cm)、sepal width (cm)、petal length (cm)、petal width (cm)，三种不同的类别0、1、2分别对应于Iris-Setosa、Iris-Versicolour和Iris-Virginica这三类。

为了方便做可视化，我们对数据进行精简，只选取2、3两列来训练与预测模型。我们取petal length (cm)和petal width (cm)这两个特征来训练和预测。

由于Iris数据集的特征为连续值，因此我们需要将其分成多个区间，从而将连续数值离散化。

1
2
3
4
5
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import KBinsDiscretizer
1
2
3
4
5
X,y=load_iris(return_X_y=True)
X=X[:,2:4]
Discretizer=KBinsDiscretizer(n_bins=5)
Discretizer.fit(X)
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3)
1
2
3
clf=MultinomialNB()
clf.fit(Discretizer.transform(train_x),train_y)
pred_y=clf.predict(Discretizer.transform(test_x))

为了方便分析，我们将测试数据以及模型的分类边界绘制在同一幅图中：

1
2
3
X_mesh,Y_mesh=np.meshgrid(np.linspace(0,8,200),np.linspace(0,5,100))
XY_mesh=np.concatenate([X_mesh.reshape(-1,1),Y_mesh.reshape(-1,1)],axis=1)
mesh=clf.predict(Discretizer.transform(XY_mesh))
1
2
3
4
5
6
7
8
9
10
fig=plt.figure(figsize=(8,6))
axes=fig.subplots(1,1)
axes.set_xlabel('sepal length (cm)')
axes.set_ylabel('sepal width (cm)')
contour=axes.contourf(X_mesh,Y_mesh,mesh.reshape(X_mesh.shape),cmap='Greys')
fig.colorbar(contour,ax=axes)
axes.scatter(test_x[test_y==0][:,0],test_x[test_y==0][:,1],label='Iris-Setosa')
axes.scatter(test_x[test_y==1][:,0],test_x[test_y==1][:,1],label='Iris-Versicolour')
axes.scatter(test_x[test_y==2][:,0],test_x[test_y==2][:,1],label='Iris-Virginica')
axes.legend()
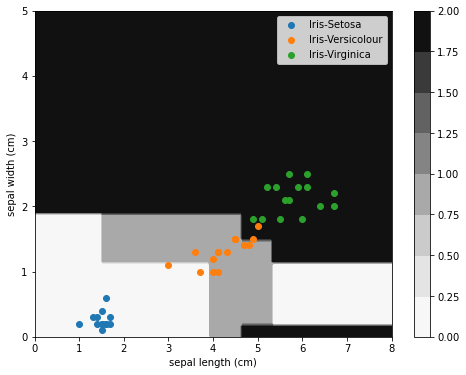
朴素贝叶斯

从图中可以观察到，由于朴素贝叶斯模型假设特征之间相互独立，因此它的分类边界由若干条与坐标轴平行的线段构成。而且同一类别可能会对应于多个不同的区域。

参考

  1. 统计学习方法，李航
  2. https://blog.csdn.net/yzz595512448/article/details/88911741