定义
在传统的DNN、CNN等前向反馈神经网络模型中,数据从输入层传到若干隐藏层最后再流向输出层,每层之间的节点是无连接的。这些模型在处理图像、表格等数据上面表现突出,但是在面对序列型数据如文本、语音、股票等上下文相关的数据时却无能为力。
例如我们要翻译下面两句话中的Apple这个单词:
第一句话:I like eating apple!(我喜欢吃苹果!)
第二句话:The Apple is a great company!(苹果真是一家很棒的公司!)
我们都知道第一个apple是一种水果,第二个apple是苹果公司。假设现在有大量的已经标记好的数据以供训练模型,如果我们使用全连接神经网络,做法是把apple这个单词的特征向量输入到模型中。但我们的语料库中,有的apple对应的标签是水果,有的标签是公司,这将导致模型在训练的过程中,预测的准确程度取决于训练集中哪个标签多一些,因此这样的模型对于我们来说完全没有价值。其中问题就出在了我们没有结合上下文去训练模型,而是单独的在训练apple这个单词。
为了解决上述问题,人们发明了循环神经网络(Recurrent Neural Network,RNN),它是一类具有短期记忆能力的神经网络。在循环神经网络中,神经元不但可以接受其它神经元的信息,也可以接受自身的信息,形成具有环路的网络结构。循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上。循环神经网络的参数学习可以通过随时间反向传播算法(BPTT)来学习。随时间反向传播算法即按照时间的逆序,将错误信息一步步地往前传递。
网络结构
RNN的基本结构如下图所示,其中左图为RNN本身的结构,右图是它按照序列展开之后的结构:

图中的一个圈表示神经网络中的一层,也就是说一个圈对应的是网络中一层的所有神经元。\(\boldsymbol x_t\)表示\(t\)时刻的输入,\(\boldsymbol o_t\)表示\(t\)时刻的输出,\(\boldsymbol s_t\)表示\(t\)时刻的记忆(它们都为行向量),\(U,V,W\)为代表网络参数的矩阵。根据图中所示的结构,可以使用下面的计算公式计算\(t\)时刻的记忆和输出: \[ \boldsymbol{s}_t=f_1(U\boldsymbol{x}_{t-1}^T+W\boldsymbol{s}_{t-1}^T+b) \\ \boldsymbol{o}_t=f_2(V\boldsymbol{s}_t^T+c) \] 在实际使用中,针对不同的目的,可以选用下面4种模式中的一种:
一对多:一个输入对应于多个输出。这种模式通常用于图片的特征识别,即输入一张图片然后输出一个文本序列。
![vcim5uu737]()
多对一:多个输入对应于一个输出,多用于文本分类或者视频分类
![qwsm2mhpfw]()
多对多:其中又分为两个不同的模式
输入序列结束之后得到输出序列,这种结构常被用于机器翻译等任务。
![yv5d4ikvmb]()
每一个输入都对应于一个输出,这种结构常被用于序列标注等任务。
![d8nf8e9lle]()
网络训练
BPTT
RNN的训练是通过基于时间的反向传播(Back-Propagation Through Time, BPTT)来进行的。它的流程大致可以表示为下图:

我们将全局误差记作\(E=\sum_{i=0}^{t}E_i\),那么每个权重的梯度可以表示为下面的形式: \[ \nabla V=\frac{\partial E}{\partial V}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial V} \\ \nabla c=\frac{\partial E}{\partial c}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial c} \\ \nabla U=\frac{\partial E}{\partial U}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial U} \\ \nabla W=\frac{\partial E}{\partial W}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial W} \\ \nabla b=\frac{\partial E}{\partial b}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial b} \] \(\nabla V\)和\(\nabla c\)不依赖于之前的状态,因此可以直接通过下面的公式计算: \[ \nabla V=\frac{\partial E}{\partial V}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial \boldsymbol{o}_i}\frac{\partial \boldsymbol{o}_i}{\partial V} \\ \nabla c=\frac{\partial E}{\partial c}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial \boldsymbol{o}_i}\frac{\partial \boldsymbol{o}_i}{\partial c} \] 但是\(\nabla U,\nabla W,\nabla b\)依赖于之前的状态,在反向传播时,某一序列位置\(t\)的梯度损失由当前位置的输出对应的梯度损失和序列位置\(t+1\)时的梯度损失两部分共同决定。为了计算方便,我们定义序列\(t\)位置隐藏状态\(\boldsymbol s_t\)的梯度为\(\boldsymbol \delta_t\),则它的表达式如下: \[ \boldsymbol \delta_t=\frac{\partial E}{\partial \boldsymbol s_t}=\frac{\partial E}{\partial \boldsymbol o_t}\frac{\partial \boldsymbol o_t}{\partial \boldsymbol s_t}+\frac{\partial E}{\partial \boldsymbol s_{t+1}}\frac{\partial \boldsymbol s_{t+1}}{\partial \boldsymbol s_t} \] 根据这一定义,在序列的末端\(\tau\),有:\(\boldsymbol \delta_\tau=\frac{\partial E}{\partial \boldsymbol s_\tau}=\frac{\partial E}{\partial \boldsymbol o_\tau}\frac{\partial \boldsymbol o_\tau}{\partial \boldsymbol s_\tau}\)。
定义了\(\boldsymbol \delta_t\)之后,接下来便可以写出\(\nabla U,\nabla W,\nabla b\)的表达式: \[ \nabla U=\frac{\partial E}{\partial U}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial \boldsymbol s_t}\frac{\partial \boldsymbol s_t}{\partial U}=\sum_{i=0}^{t}\boldsymbol \delta_t\frac{\partial \boldsymbol s_t}{\partial U}\\ \nabla W=\frac{\partial E}{\partial W}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial \boldsymbol s_t}\frac{\partial \boldsymbol s_t}{\partial W}=\sum_{i=0}^{t}\boldsymbol \delta_t\frac{\partial \boldsymbol s_t}{\partial W}\\ \nabla b=\frac{\partial E}{\partial b}=\sum_{i=0}^{t}\frac{\partial E_i}{\partial \boldsymbol s_t}\frac{\partial \boldsymbol s_t}{\partial b}=\sum_{i=0}^{t}\boldsymbol \delta_t\frac{\partial \boldsymbol s_t}{\partial b} \] 在上述表达式中,\(\frac{\partial \boldsymbol{o}_i}{\partial V}\),\(\frac{\partial \boldsymbol{o}_i}{\partial c}\),\(\frac{\partial \boldsymbol o_t}{\partial \boldsymbol s_t}\),\(\frac{\partial \boldsymbol s_{t+1}}{\partial \boldsymbol s_t}\),\(\frac{\partial \boldsymbol s_t}{\partial U}\),\(\frac{\partial \boldsymbol s_t}{\partial W}\)和\(\frac{\partial \boldsymbol s_t}{\partial b}\)取决于\(f_1\)和\(f_2\)的函数表达式,在使用不同的激活函数时它们的表达式也有所不同。
梯度消失与梯度爆炸
从上述的推导过程中也可以看到,我们在计算\(\boldsymbol \delta_t\)的时候,其中一项为\(\frac{\partial E}{\partial \boldsymbol s_{t+1}}\frac{\partial \boldsymbol s_{t+1}}{\partial \boldsymbol s_t}\),也就是与\(t+1\)时刻的状态有关;而以此类推,\(\frac{\partial E}{\partial \boldsymbol s_{t+1}}\)这一项也与\(t+2\)时刻的状态有关;如此向前直到序列的末端\(\tau\)。
因此,如果我们考虑\(t=0\)的极端情况,此时\(\boldsymbol \delta_0\)中会包含有\(\prod_{t=0}^{\tau -1}\frac{\partial \boldsymbol s_{t+1}}{\partial \boldsymbol s_t}\)这样的累乘式。如果在模型中使用的是\(\tanh\)这样的激活函数,由于它的导数值在0-1之间,因此在序列过长的情况下这个累乘表达式的值便会接近于0,从而导致梯度消失的现象;而如果累乘式中存在一些导数较大的项,则它们在累乘之后也很容易出现梯度爆炸的现象。
LSTM
长短记忆神经网络(LSTM)被用于解决RNN中梯度消失的问题。一个LSTM单元的计算过程如下图所示:

LSTM的核心在于cell state,从上图中可以看出,cell state的更新过程并没有太多的运算,仅仅是做了一些小的线性变换。因此,这就使得信息在从这条路径上经过时,只被做一些微小的修改。通过这种方式,便实现了长期记忆的效果。
接下来,我们对LSTM中状态的更新过程进行详细地拆解:
第一步为遗忘门操作,这一步是决定需要丢弃掉cell state中的哪些信息。例如在语言模型中,我们需要根据以前的信息来预测下一个单词。当遇到一个新的名词时,我们可能需要丢掉旧的名词信息。此时,我们便需要丢弃掉cell state中包含的旧名词信息。遗忘门的计算过程如下图所示:

第二步为输入门操作,这一步操作的目的是决定需要在cell state中存储哪些信息。同样以语言模型为例,当我们遇到一个新的名词时,便需要将其加入到cell state中,从而更新其信息。这一步的操作如下:,

在进行完上述的两步操作之后,我们便可以最终完成对cell state的更新,相当于是删除旧信息的同时再把新信息添加进去:

最后一步是输出门操作,这一步的目的是决定输出的内容。仍以上述的语言模型为例,当看到一个名词时,考虑到它后面很可能会出现动词,因此需要输出与动词相关的信息。例如输出名词是单数还是复数,或者人称等信息,以便后续对动词的处理。计算过程如下:

GRU
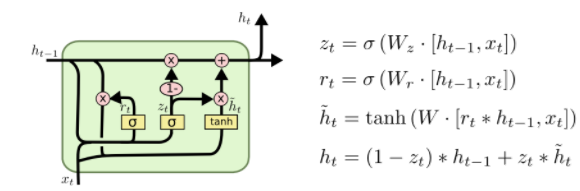
GRU可以看成是LSTM的简化版,它的计算过程可以用下图表示:

在GRU模型中只有两个门,分布为更新门和重置门。更新门用于控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门控制前一状态有多少信息被写入到当前的候选集\(\tilde{h}_t\)上,重置门越小,前一状态的信息被写入的越少。它的计算过程如下:
参考
- https://zhuanlan.zhihu.com/p/123211148
- https://blog.csdn.net/qq_39422642/article/details/78676567
- https://cloud.tencent.com/developer/article/1088995
- https://www.cnblogs.com/pinard/p/6509630.html
- https://blog.csdn.net/lzw66666/article/details/113132149
- https://zhuanlan.zhihu.com/p/115823190
- http://colah.github.io/posts/2015-08-Understanding-LSTMs/
- https://www.cnblogs.com/jiangxinyang/p/9376021.html




