原理
线性判别分析(Linear Discrimination Analysis, LDA)是一种监督学习算法,属于线性模型的一种,这一算法可以用于对样本进行分类,也可以用于对样本进行降维,但是目前比较多的应用是降维。下文中将使用两种不同的思路推导其原理,并介绍在Sklearn中它的使用方法。
推导1:贝叶斯定理+高斯分布假设
假设\(f_{k}(x)\)代表样本\(X=x\)满足类别\(G=k\)的条件概率密度;令\(\pi _k\)代表\(x\)属于第\(k\)个类别的先验概率,则它满足\(\sum_{k=1}^{K}\pi _k=1\)。通过使用贝叶斯定理可以得到: \[ Pr(G=k|X=x)=\frac{f_k(x)\pi_k}{\sum_{\ell=1}^{K}f_{\ell}(x)\pi_\ell} \] 如果我们假设每个类别的概率密度函数都是如下的多变量高斯分布,即: \[ f_k(x)=\frac{1}{(2\pi)^{p/2}|\Sigma_{k}|^{1/2}}e^{-\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k)} \]
LDA
线性判别分析在基于上述假设的基础上又做了另一个额外的假设:每个类别有着相同的协方差矩阵,即\(\Sigma_{k}=\Sigma~\forall k\)。此时,如果比较样本\(x\)属于类别\(G=k\)和\(G=\ell\)的概率之比(由于表达式中出现了\(e\)的指数,因此我们对这一比值求对数以方便比较),可得如下结果: \[ \begin{aligned} \log \frac{Pr(G=k|X=x)}{Pr(G=\ell|X=x)}=&\log \frac{f_k(x)}{f_\ell(x)}+\log \frac{\pi_k}{\pi_\ell} \\ =& \log \frac{\pi_k}{\pi_\ell}-\frac{1}{2}(\mu_k+\mu_\ell)^T\Sigma^{-1}(\mu_k-\mu_\ell)+x^T\Sigma^{-1}(\mu_k-\mu_\ell) \end{aligned} \] 从中可以看到,由于协方差矩阵相等,关于\(x^2\)的表达式在计算的过程中被消去,最终可得二者的比值是一个关于\(x\)的线性方程。这一结果说明,类别\(k\)与类别\(\ell\)的决策边界,即\(Pr(G=k|X=x)=Pr(G=\ell|X=x)\)处,为一条直线(如果维度更高则为超平面)。由于在推导的过程中\(k\)和\(\ell\)可以为任意的类别,因此这一结论对于所有类别的决策边界都成立。下图所示为一组二维数据,其中共包含三个类别,它们所形成的决策边界:
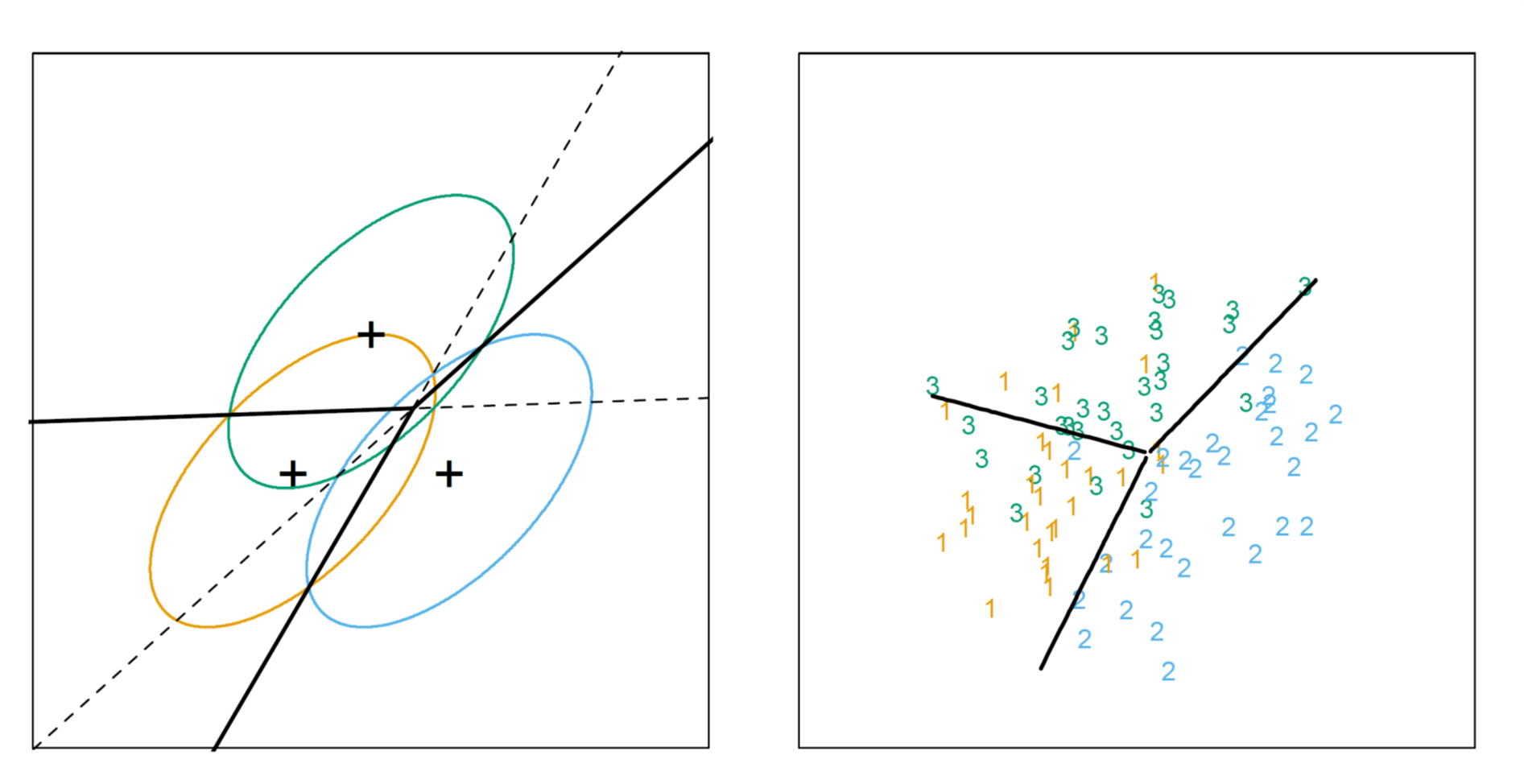
由上式可以定义下面的线性判别方程: \[ \delta_k(x)=x^T\Sigma^{-1}\mu_k-\frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k+\log\pi_k \] 最终\(x\)的类别可以通过计算\(G(x)=\text{argmax}_k\delta_k(x)\)来判断。
在实际操作中,由于高斯分布的参数未知,因此需要我们使用训练数据集,按照下面的公式进行估算:
- \(\hat{\pi}_k=N_k/N\),其中\(N_k\)代表第\(k\)个类别的样本数
- \(\hat{\mu}_k=\sum_{g_i=k}x_i/N_k\)
- \(\hat{\Sigma}=\Sigma_{k=1}^{K}\Sigma_{g_i=k}(x_i-\hat{\mu}_k)(x_i-\hat{\mu}_k)^T/(N-K)\)
QDA
如果去掉\(\Sigma_k\)相等的假设,那么此时在计算\(\log \frac{Pr(G=k|X=x)}{Pr(G=\ell|X=x)}\)时,关于\(x\)的二次项就不会被消去,此时被称为是二次判别分析(Quadratic Discriminant Analysis, QDA)。
相应地,我们也可以定义如下的二次判别方程: \[ \delta_k(x)=-\frac{1}{2}\log |\Sigma_k|-\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k)+\log \pi_k \] 此时,类别\(k\)和类别\(l\)的决策边界由二次方程\(\delta_k(x)=\delta_\ell(x)\)决定。下图为QDA所形成的决策边界的示意图:
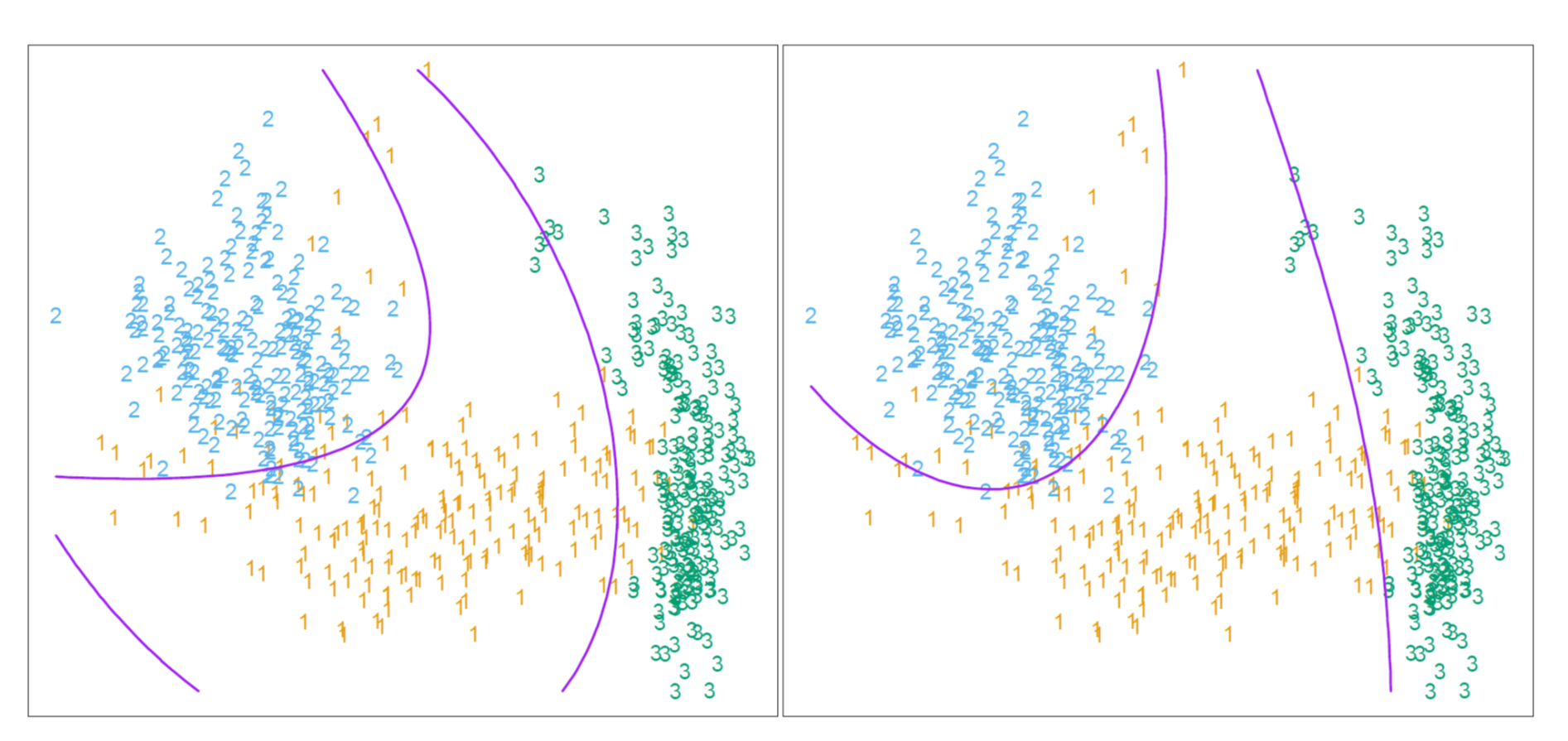
RDA
一种综合了LDA和QDA的方法被称为RDA(Regularized Discriminant Analysis),在这种方法中,协方差矩阵被表示为下面的格式: \[ \hat{\Sigma}_k(\alpha)=\alpha\hat{\Sigma}_k+(1-\alpha)\hat{\Sigma} \] 其中,\(\alpha \in [0,1]\)为模型的超参数。通过这一定义,便获得了一系列在LDA与QDA之间连续变化的模型。
说明
虽然在上述的推导过程中假设原始数据的概率分布满足多维高斯分布,但是在实际使用中则没有这一限制。需要注意的是,如果原始数据的概率分布与高斯分布差距过大,则可能会影响模型的表现。
推导2:瑞利商最大化
另一种推导方法的基本思想是设法将训练样本投影到一条直线上,使得同类样本的投影点尽可能地接近、异类样例的投影点尽可能地远离。而在对新样本进行分类时,将其投影到同样的直线上,再根据投影点的位置来确定新样本的类别。下图为LDA在二维空间内的一个示例:
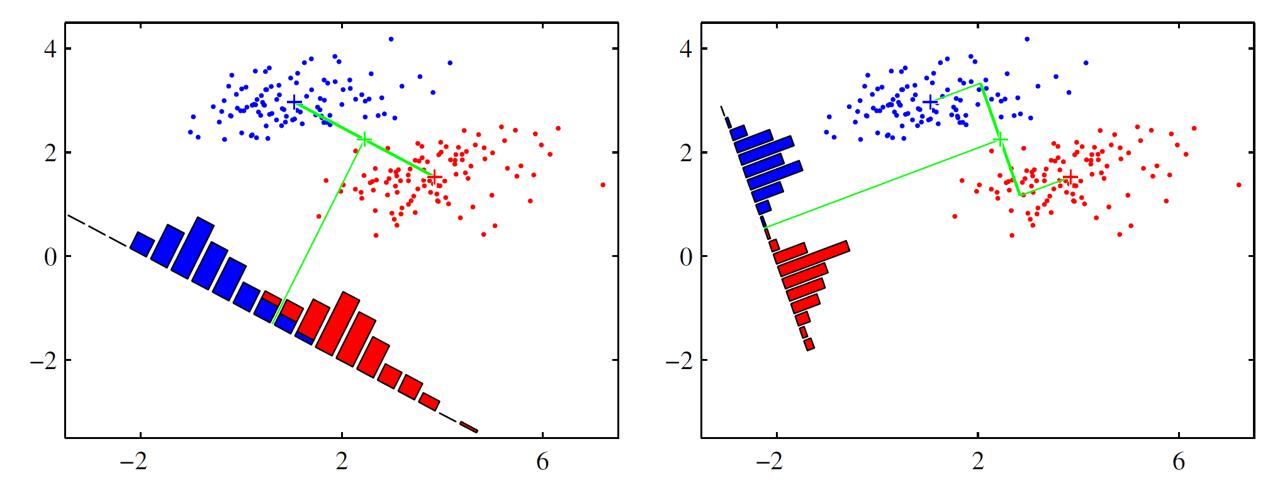
二分类LDA
下面我们先以二分类进行推导,再推广至多分类问题。给定数据集\(D=\{(\boldsymbol{x}_i,y_i)\}_{i=1}^{m}\),其中\(y_i \in \{0,1\}\)。令\(X_i\)表示第\(i\in \{0,1\}\)个类别的集合;\(\boldsymbol{\mu}_i\)表示第\(i\in \{0,1\}\)个类别的均值向量;\(\boldsymbol{C}_i\)表示第\(i\in \{0,1\}\)个类别的协方差矩阵,其中\(\boldsymbol{C}_i=\sum_{\boldsymbol{x}\in X_i}(\boldsymbol{x}-\boldsymbol{\mu}_0)(\boldsymbol{x}-\boldsymbol{\mu}_0)^{T}\)。
假设将数据投影到直线\(\boldsymbol{w}\)上,则两类样本的中心在直线上的投影分别为\(\boldsymbol{w}^{T}\boldsymbol{\mu}_0\)和\(\boldsymbol{w}^{T}\boldsymbol{\mu}_1\)。如果将所有样本点都投影到直线上,那么投影后两类样本的协方差分别为\(\boldsymbol{w}^{T}\boldsymbol{C}_0\boldsymbol{w}\)和\(\boldsymbol{w}^{T}\boldsymbol{C}_1\boldsymbol{w}\)。由于直线属于一维空间,因此\(\boldsymbol{w}^{T}\boldsymbol{\mu}_0\)、\(\boldsymbol{w}^{T}\boldsymbol{\mu}_1\)、\(\boldsymbol{w}^{T}\boldsymbol{C}_0\boldsymbol{w}\)和\(\boldsymbol{w}^{T}\boldsymbol{C}_1\boldsymbol{w}\)的计算结果都为实数。
如果要让同类样本的投影点尽可能接近,就是让同类样本投影点的协方差尽可能地小,即\(\boldsymbol{w}^{T}\boldsymbol{C}_0\boldsymbol{w}+\boldsymbol{w}^{T}\boldsymbol{C}_1\boldsymbol{w}\)尽可能小;而要让异类样本的投影点尽可能远离,则需要让类中心之间的距离尽可能地大,即\(||\boldsymbol{w}^{T}\boldsymbol{\mu}_0-\boldsymbol{w}^{T}\boldsymbol{\mu}_1||_{2}^{2}\)尽可能大。也就是说,我们要计算如下广义瑞利商表达式的最大值: \[ \frac{||\boldsymbol{w}^{T}\boldsymbol{\mu}_0-\boldsymbol{w}^{T}\boldsymbol{\mu}_1||_{2}^{2}}{\boldsymbol{w}^{T}\boldsymbol{C}_0\boldsymbol{w}+\boldsymbol{w}^{T}\boldsymbol{C}_1\boldsymbol{w}}=\frac{\boldsymbol{w}^{T}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^{T}\boldsymbol{w}}{\boldsymbol{w}^{T}(\boldsymbol{C}_0+\boldsymbol{C}_1)\boldsymbol{w}} \]
为了表达的简便,我们定义“类内散度矩阵”\(\boldsymbol{S}_w=\boldsymbol{C}_0+\boldsymbol{C}_1\)以及“类间散度矩阵”\(\boldsymbol{S}_b=(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^{T}\),则优化问题可以重写为: \[ \max \frac{\boldsymbol{w}^{T}\boldsymbol{S}_{b}\boldsymbol{w}}{\boldsymbol{w}^{T}\boldsymbol{S}_{w}\boldsymbol{w}} \]
在上式中,分子和分母都是关于\(\boldsymbol{w}\)的二次项,因此优化问题的解与\(\boldsymbol{w}\)的长度无关,只与其方向有关。因此我们令\({\boldsymbol{w}^{T}\boldsymbol{S}_{w}\boldsymbol{w}}=1\),则优化问题等价于: \[ \min_{\boldsymbol{w}}~-\boldsymbol{w}^{T}\boldsymbol{S}_{b}\boldsymbol{w} \\ \text{s.t.}~\boldsymbol{w}^{T}\boldsymbol{S}_{w}\boldsymbol{w}=1 \]
使用拉格朗日乘子法,上式等价于: \[ \boldsymbol{S}_{b}\boldsymbol{w}=\lambda \boldsymbol{S}_{w}\boldsymbol{w} \]
其中\(\lambda\)为拉格朗日乘子。根据矩阵运算的结合律,\(\boldsymbol{S}_{b}\boldsymbol{w}=(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^{T}\boldsymbol{w}=(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)[(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^{T}\boldsymbol{w}]\),中括号内的计算结果为一个实数,因此\(\boldsymbol{S}_{b}\boldsymbol{w}\)的方向恒为\(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1\),因此我们不妨假设\(\boldsymbol{S}_{b}\boldsymbol{w}=\lambda(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)\)。将其代入待优化表达式,可得: \[ \boldsymbol{w}=\boldsymbol{S}_{w}^{-1}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1) \]
考虑到数值解的稳定性,实际操作中通常是对\(\boldsymbol{S}_{w}\)做奇异值分解,然后对分解后的结果取逆。
备注:瑞利商的定义可以参考https://blog.csdn.net/wyl1813240346/article/details/78548274
多分类LDA
上面推导的二分类LDA可以推广至多分类任务中。假定存在\(N\)个类,且第\(i\)个类的样本数量为\(m_i\)。我们设\(\boldsymbol{\mu}\)为所有示例的均值向量。此时我们重新定义类内散度矩阵的表达式为: \[ \boldsymbol{S}_{w}=\sum_{i=1}^{N}\boldsymbol{S}_{w_i}=\sum_{i=1}^{N}\sum_{\boldsymbol{x}\in X_{i}}(\boldsymbol{x}-\boldsymbol{\mu}_i)(\boldsymbol{x}-\boldsymbol{\mu}_i)^{T} \]
同时我们也重新定义类间散度矩阵的表达式为: \[ \boldsymbol{S}_{b}=\sum_{i=1}^{N}m_{i}(\boldsymbol{\mu}_i-\boldsymbol{\mu})(\boldsymbol{\mu}_i-\boldsymbol{\mu})^{T} \]
此时的优化目标为: \[ \max_{\boldsymbol{W}}\frac{\text{tr}(\boldsymbol{W}^{T}\boldsymbol{S}_{b}\boldsymbol{W})}{\text{tr}(\boldsymbol{W}^{T}\boldsymbol{S}_{w}\boldsymbol{W})} \]
其中\(\boldsymbol{W}\in \mathbb{R}^{d\times (N-1)}\),\(\text{tr}(\cdot)\)表示矩阵的迹。此时\(\boldsymbol{W}\)的闭式解为\(\boldsymbol{S}_{w}^{-1}\boldsymbol{S}_{b}\)的\(N-1\)个最大广义特征值所对应的特征向量所组成的矩阵。
如果将\(W\)视为一个投影矩阵,则多分类LDA将样本投影到\(N-1\)维空间,这一维度通常远小于数据原有的特征数量。因此,可以通过这一投影来减小样本的维数(最多降到\(N-1\)维),故LDA常常也被看作是一种经典的监督降维技术。
在用作降维时,LDA与PCA的比较可以总结如下:
- LDA是有监督的降维方法,而PCA是无监督的降维方法
- LDA降维最多降到\(N-1\)的维数,而PCA没有这个限制。
- LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
使用示例
降维
Sklearn中提供了LinearDiscriminantAnalysis类,可以用LDA来对原始数据进行降维,使用方法如下所示:
1 | from sklearn.discriminant_analysis import LinearDiscriminantAnalysis |
array([[-8.06179978, 0.30042062],
[-7.12868772, -0.78666043],
[-7.48982797, -0.26538449],
...,
[ 4.9677409 , 0.82114055],
[ 5.88614539, 2.34509051],
[ 4.68315426, 0.33203381]])分类
我们使用Sklearn自带的Iris数据集,来演示如何用sklearn中的支持向量机分类器做分类任务。
Iris数据集的四个特征分别为:sepal length (cm)、sepal width (cm)、petal length (cm)、petal width (cm),三种不同的类别0、1、2分别对应于Iris-Setosa、Iris-Versicolour和Iris-Virginica这三类。
为了方便做可视化,我们对数据进行精简,只选取2、3两列来训练与预测模型。我们取petal length (cm)和petal width (cm)这两个特征来训练和预测。
1 | from sklearn.datasets import load_iris |
1 | X,y=load_iris(return_X_y=True) |
我们同时使用LDA和QDA进行分类,并将两模型的分类边界与预测数据点绘制在同一幅图中:
1 | X_mesh,Y_mesh=np.meshgrid(np.linspace(0,8,200),np.linspace(0,5,100)) |
1 | fig=plt.figure(figsize=(10,3)) |
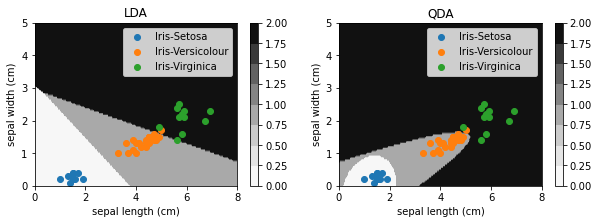
从中可以看到,LDA形成了线性的分类边界,而QDA则是抛物线型的分类边界。
参考
- The Elements of Statistical Learning
- 机器学习,周志华
- Pattern Recognition and Machine Learning
- https://www.cnblogs.com/pinard/p/6244265.html
