"> "> 机器学习-主成分分析 | Yufei Luo's Blog

Yufei Luo's Blog

But I was so much older then, I am younger than that now.

Yufei Luo's Blog

机器学习-主成分分析

发表于 更新于 分类于 ， 阅读次数：
本文字数： 13k 阅读时长 ≈ 11 分钟

原理

主成分分析(Principle Components Analysis, PCA)属于无监督学习算法，它的想法是用一个\(q\)维的数据去尽可能地近似表达原本\(p(p>q)\)维的数据。

推导1：最小重建误差

我们将原始数据记作\(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_N\)，为一系列的\(p\)维行向量。假设现在构造了一个用来近似表示\(\boldsymbol{x}_i\)的模型：\(f(\boldsymbol{\lambda})=\boldsymbol{\mu} + \boldsymbol{\lambda}\boldsymbol{V}_{q}^T\)，其中\(\boldsymbol{\mu}\)是一个\(p\)维空间中的行向量；\(\boldsymbol{V}_q=\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_q\}\)一个\(p\times q\)的矩阵，\(\{\boldsymbol{v}_i\}\)两两正交的单位向量；函数的输入参数\(\boldsymbol{\lambda}\)即为压缩后的\(q\)维行向量（\(q\le p\)）。

\(f(\boldsymbol{\lambda})\)的目的是尽量地将压缩后的\(q\)维向量还原为\(p\)维向量，并且使得重构误差尽可能地小，用数学公式可以表达为：

\[ \arg \min _{\mu,\boldsymbol{V}_q,{\boldsymbol{\lambda}_i}} \sum_{i=1}^{N}||\boldsymbol{x}_i-\boldsymbol{\mu} -\boldsymbol{\lambda}_i\boldsymbol{V}_q^T||^2 \]

通过对上式中的\(\boldsymbol{\mu}\)和\(\boldsymbol{\lambda}_i\)求偏导，取偏导等于0作为极值点的条件，从中可求得： \[ \hat{\boldsymbol{\mu}}=\bar{\boldsymbol{x}} \]

\[ \hat{\boldsymbol{\lambda _{i}}}=(\boldsymbol{x_{i}}-\boldsymbol{\bar{x}})\boldsymbol{V}_{q} \]

将上述结果带入待优化表达式，此时优化目标变为： \[ \arg \min _{\boldsymbol{V}_q} \sum_{i=1}^{N}||(\boldsymbol{x}_i-\boldsymbol{\bar{x}})-(\boldsymbol{x}_{i}-\boldsymbol{\bar{x}})\boldsymbol{V}_{q}\boldsymbol{V}_q^T||^2 \]

为了简便起见，令\(\boldsymbol{\bar{x}}=\boldsymbol{0}\)(如果不满足此条件可以对原始数据进行平移)。式中的\(\boldsymbol{V}_{q}\boldsymbol{V}_q^{T}\)是一个\(p\times p\)的矩阵，它被称为投影矩阵，记作\(\boldsymbol{H}_q\)，它将每个\(\boldsymbol{x}_i\)投影至它秩为\(q\)的重建向量\(\boldsymbol{x}_i\boldsymbol{H}_q\)上，即\(\boldsymbol{x}_i\)在\(\boldsymbol{V}_q\)的列向量张成的子空间内的投影。

备注：这里的投影可以按照如下两步理解

  1. \(\boldsymbol{x}_i\boldsymbol{V}_{q}\)：矩阵\(\boldsymbol{V}_{q}\)的每一列可以认为是一个基，也就是说这个矩阵对应于一个正交基空间（\(q\)维空间。由于每个正交基都是\(p\)维的，因此可以理解成\(p\)维空间内的一个\(q\)维子空间）。这一步相当于是算\(\boldsymbol{x}_i\)在这组正交基上面每个基向量上的内积（相当于矩阵\(\boldsymbol{V}_{q}\)所对应的\(q\)维空间内的坐标）
  2. \((\boldsymbol{x}_i\boldsymbol{V}_{q})\boldsymbol{V}_q^{T}\)：上一步已经计算出\(q\)维空间内的坐标。这一步是根据正交基向量及其坐标，恢复出\(p\)维空间内的向量表示。

写成矩阵形式，优化目标为（\(\boldsymbol X\)是个\(N\times p\)维的向量，）： \[ \arg \min _{\boldsymbol{V}_q} ||\boldsymbol{X}-\boldsymbol{X}\boldsymbol{V}_{q}\boldsymbol{V}_q^{T}||_F^2 \] 这里的\(F\)范数可以拿矩阵的迹替换掉： \[ \arg \min _{\boldsymbol{V}_q} \text{tr}\left((\boldsymbol{X}-\boldsymbol{X}\boldsymbol{V}_q\boldsymbol{V}_{q}^{T})^T(\boldsymbol{X}-\boldsymbol{X}\boldsymbol{V}_q\boldsymbol{V}_{q}^{T})\right) \] 将括号内的部分乘开，并去掉与\(\boldsymbol V_q\)无关的项，可以得到等价的优化目标： \[ \arg \max _{\boldsymbol{V}_q} \text{tr}\left(\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{V}_q\boldsymbol{V}_{q}^{T}\right) \] 根据矩阵迹的性质\(\text{tr}(\boldsymbol A \boldsymbol B)=\text{tr}(\boldsymbol B \boldsymbol A)\)，上式等价于 \[ \arg \max _{\boldsymbol{V}_q} \text{tr}\left(\boldsymbol{V}_{q}^{T}\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{V}_q\right) \] 表达式\(\text{tr}\left(\boldsymbol{V}_{q}^{T}\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{V}_q\right)\)等于\(\sum_{i=1}^q \boldsymbol v_i^T\boldsymbol X^T\boldsymbol X\boldsymbol v_i\)，其中\(\boldsymbol v_i\)代表矩阵\(\boldsymbol V_q\)的第\(i\)个列向量。即\(\sum_{i=1}^q <\boldsymbol X\boldsymbol v_i,\boldsymbol X\boldsymbol v_i>\)。也就是说，如果要使得这一表达式取得最大，\(\boldsymbol v_i\)需要取\(\boldsymbol{X}^T\boldsymbol{X}\)的最大的\(q\)个特征值所对应的特征向量。

根据奇异值分解的定义，\(\boldsymbol{V}_q\)便可以通过奇异值分解来计算。首先，将所有中心化的\(\boldsymbol{x}_i\)按行堆叠成一个\(N\times p\)的矩阵\(\boldsymbol{X}\)，通过将\(\boldsymbol{X}\)做奇异值分解为\(\boldsymbol{X}=\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^T\)的形式。其中，\(\boldsymbol{U}\)为一个\(N\times N\)的正交矩阵，\(\boldsymbol{V}\)是一个\(p\times p\)的正交矩阵，\(\boldsymbol{\Sigma}\)是一个\(N\times p\)的对角矩阵且对角元素从左上到右下逐渐变小。

对于秩为\(q\)的正交矩阵\(\boldsymbol{V}_q\)，我们只需要取\(\boldsymbol{V}\)的前\(q\)列即可。相应地，\(N\)个压缩后的向量\(\hat{\boldsymbol{\lambda _{i}}}\)是通过保留矩阵\(\boldsymbol{U}\boldsymbol{\Sigma}\)的前\(q\)列，然后每一行便对应于\(\boldsymbol{x}_i\)压缩后的向量\(\hat{\boldsymbol{\lambda _{i}}}\)。

推导2：方差最大

PCA的另一种推导方式是从最大方差的角度去考虑，它的出发点是在数据降维之后，能够在降维后的特征上保持尽可能大的方差。这样在降维后的数据上，能够使得数据点尽可能地分散。

假设\(\boldsymbol{x}=(x_1,x_2,\dots,x_m)\)是\(m\)维的随机变量，它的均值向量为\(\boldsymbol{\mu}=E(\boldsymbol{x})=(\mu_1,\mu_2,\dots,\mu_m)\)，协方差矩阵为\(\Sigma=\text{cov}(\boldsymbol{x},\boldsymbol{x})=E[(\boldsymbol{x}-\boldsymbol{\mu})^T(\boldsymbol{x}-\boldsymbol{\mu})]\)。考虑由\(m\)维随机变量\(\boldsymbol{x}\)到\(m\)维随机变量\(\boldsymbol{y}=(y_1,y_2,\dots,y_m)\)的线性变换：\(y_i=\boldsymbol{x}\alpha_i^T=\alpha_{1i}x_1+\alpha_{2i}x_2+\dots+\alpha_{mi}x_m\)，其中\(\alpha_i=(\alpha_{1i},\alpha_{2i},\dots,\alpha_{mi}),i=1,2,\dots,m\).

如果上述的线性变换满足以下三个条件：

  1. 系数向量\(\alpha_i\)为单位向量。这一条件表明线性变换是正交变换，\(\{\alpha_i\}\)是一组标准正交基
  2. 变量\(y_i\)与\(y_j\)互不相关；
  3. 变量\(y_1\)是\(\boldsymbol{x}\)的所有线性变换中方差最大的；\(y_2\)是与\(y_1\)不相关的\(\boldsymbol{x}\)的所有线性变换中方差最大的；以此类推，\(y_i\)是与\(y_1,y_2,\dots,y_{i-1}\)都不相关的\(\boldsymbol{x}\)的所有线性变换中方差最大的。

此时分别称\(y_1,y_2,\dots,y_i\)为\(\boldsymbol{x}\)的第一、第二、……、第\(i\)主成分。

条件2和3给出了计算主成分的方法：首先在\(\boldsymbol{x}\)的所有线性变换\(\boldsymbol{x}\alpha_1^T=\sum_{i=1}^{m}\alpha_{i1}x_i\)中，在\(\alpha_{1}\alpha_{1}^{T}=1\)的条件下，求出方差最大的，得到\(\boldsymbol{x}\)的第一主成分；然后在与\(\boldsymbol{x}\alpha_1^T\)不相关的\(\boldsymbol{x}\)的所有线性变换中，\(\boldsymbol{x}\alpha_2^T=\sum_{i=1}^{m}\alpha_{i2}x_i\)中，在\(\alpha_{2}\alpha_{2}^{T}=1\)的条件下，求出方差最大的，得到\(\boldsymbol{x}\)的第二主成分；以此类推一直计算下去，可以得到\(\boldsymbol{x}\)的第\(m\)主成分。

首先我们求\(\boldsymbol{x}\)的第一主成分，即计算系数向量\(\alpha_1\)。根据定义，第一主成分是在\(\boldsymbol{x}\)的所有线性变换\(\boldsymbol{x}\alpha_1^T=\sum_{i=1}^{m}\alpha_{i1}x_i\)中，在\(\alpha_{1}\alpha_{1}^{T}=1\)的条件下，使得方差\(\text{var}(\boldsymbol{x}\alpha_1^T)=\alpha_1\Sigma \alpha_1^T\)最大的，也就是要求解下面的最优化问题： \[ \max_{\alpha_1}~\alpha_1\Sigma \alpha_1^T\\ s.t.~\alpha_{1}\alpha_{1}^{T}=1 \] 使用拉格朗日乘子法，可以定义拉格朗日函数\(\alpha_1\Sigma \alpha_1^T-\lambda(\alpha_{1}\alpha_{1}^{T}-1)\)，其中\(\lambda\)为拉格朗日乘子。将拉格朗日函数对\(\alpha_1\)求导，并令其为0，可得： \[ \Sigma \alpha_1^T-\lambda\alpha_1^T=\boldsymbol{0} \] 从上式可得，\(\lambda\)为协方差矩阵\(\Sigma\)的特征值，\(\alpha_1\)是特征值对应的单位特征向量。由于当\(\alpha_1\)取最大特征值对应的特征向量时，\(\alpha_1\Sigma \alpha_1^T\)取得最大值，此时\(\alpha_1\Sigma \alpha_1^T\)的值为协方差矩阵的最大特征值\(\lambda_1\)。

在求第二主成分时，我们需要加入额外的两个约束条件\(\alpha_1\Sigma \alpha_2^T=0\)和\(\alpha_2\Sigma \alpha_1^T=0\)。此时可求得第二主成分为协方差矩阵\(\Sigma\)的第二大特征值。以此类推，第\(k\)主成分即为协方差矩阵\(\Sigma\)的第\(k\)大特征值。

通过以上的推导可知，在对原始数据做降维时，我们只需要计算样本协方差矩阵的特征值和特征向量即可。在计算之前，需要将所有的样本中心化，即计算\(\boldsymbol{x}_{i}'=\boldsymbol{x}_{i}-\boldsymbol{\bar{x}}\)。在这一步完成之后，先计算所有特征的协方差矩阵\(\boldsymbol{C}\)，然后求出协方差矩阵的特征值\(\lambda _i\)和特征向量\(\boldsymbol{v}_i\)。通过对特征值进行排序，选出排名前\(k\)个特征值对应的特征向量。将原始的样本点投影到选出的这些特征向量上，便得到了降维后的特征。

通过协方差矩阵的特征值，我们也可以计算得到第\(k\)个主成分的方差贡献率为：\(\eta_{k}=\frac{\lambda_{k}}{\sum_{i=1}^{m}\lambda_{i}}\)。

下图是PCA将原始数据从三维降到二维的示意图：

PCA

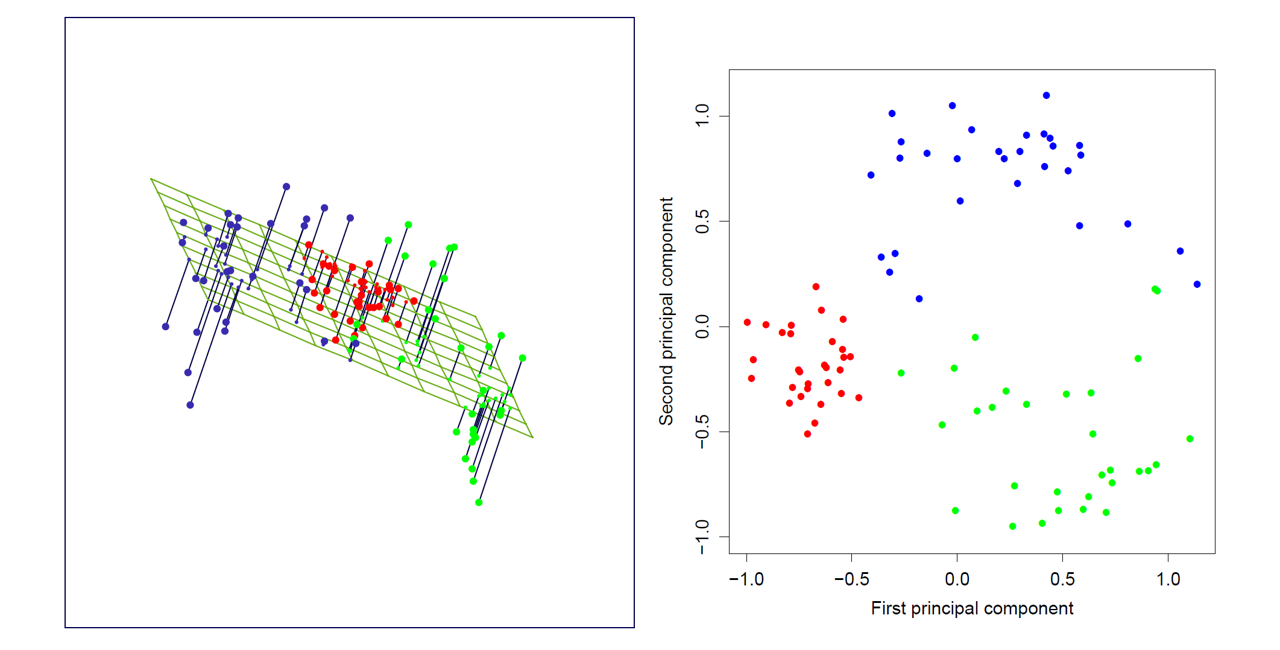
使用示例

Sklearn中的PCA类可以方便地完成主成分分析的操作，它的使用示例如下：

1
2
3
from sklearn.decomposition import PCA
pca=PCA(n_components=2) #n_components可以为整数，代表选择保留的主成分个数；也可以传入一个0-1之间的浮点数，表示所希望达到的方差贡献率，此时会自动选取特征值靠前的若干个主成分，直到方差贡献率刚好满足条件。
pca.fit_transform(iris_data)
array([[-2.68412563,  0.31939725],
       [-2.71414169, -0.17700123],
       [-2.88899057, -0.14494943],
       ...,
       [ 1.76434572,  0.07885885],
       [ 1.90094161,  0.11662796],
       [ 1.39018886, -0.28266094]])

当数据量或者是特征数目很大的时候，无论是对特征矩阵计算协方差还是做奇异值分解，所需的内存以及计算量都很大。为了解决这一问题，有两种办法。

第一种办法是使用增量PCA的办法，这种办法允许我们将数据集分批输入，每次只输入一个小批量。这种办法对大型训练集很有用，而且可以用于在线学习的情景。Sklearn提供了IncrementalPCA类，用来做增量PCA，它的使用方法如下：

1
2
3
4
5
6
from sklearn.decomposition import IncrementalPCA
n_batches=20
inc_pca=IncrementalPCA(n_components=2)
for X_batch in np.array_split(iris_data,n_batches):
    inc_pca.partial_fit(X_batch)
inc_pca.transform(X_batch)
array([[ 2.56282819,  0.28217892],
       [ 2.41842883,  0.31240878],
       [ 1.94423122,  0.18790271],
       ...,
       [ 1.76430561,  0.07992847],
       [ 1.90016469,  0.12989783],
       [ 1.38953673, -0.2751793 ]])

另一种计算PCA的方法为随机PCA。它是一种随机算法，可以快速地找到前若干个主成分的近似值。这种算法的时间复杂度与选取的主成分个数有关，而不是与特征个数有关。因此当选取的主成分个数远小于特征个数时，它比普通的PCA算法快得多。

如果要使用随机PCA，则需要在PCA类初始化的时候传入参数svd_solver='randomized'：

1
2
3
from sklearn.decomposition import PCA
rnd_pca=PCA(n_components=2,svd_solver='randomized')
rnd_pca.fit_transform(iris_data)
array([[-2.68412563,  0.31939725],
       [-2.71414169, -0.17700123],
       [-2.88899057, -0.14494943],
       ...,
       [ 1.76434572,  0.07885885],
       [ 1.90094161,  0.11662796],
       [ 1.39018886, -0.28266094]])

附：奇异值分解

证明

设矩阵\(\boldsymbol A\in \mathbb R^{m\times n}\)的秩为\(r\)。考虑矩阵\(\boldsymbol A^T \boldsymbol A\)，它的秩也为\(r\)（对\(\boldsymbol A\)做初等行变换不改变秩，两个上对角矩阵相乘也不引起秩的改变），而且\(\boldsymbol A^T\boldsymbol A\)为半正定矩阵（\(\boldsymbol x^T\boldsymbol A^T\boldsymbol A\boldsymbol x=<\boldsymbol A\boldsymbol x,\boldsymbol A\boldsymbol x>\)，相当于\(\boldsymbol A\boldsymbol x\)的内积，故有此结论）。

因此，\(\boldsymbol A^T\boldsymbol A\)的\(n\)个特征值\(\lambda_1\ge \lambda_2 \ge \cdots \ge \lambda_n\)均为非负实数，且\(\lambda_1\ge \cdots\ge \lambda_r>0\)为非零特征值。由于\(\boldsymbol A^T\boldsymbol A\)为对称矩阵，故\(n\)个特征值可以产生\(n\)个正交的特征向量（列向量）\(\boldsymbol v_1,\boldsymbol v_2,\dots,\boldsymbol v_n\)，构成\(n\)维向量空间\(\mathbb R^n\)的标准正交基。

根据特征值与特征向量的定义，有： \[ \boldsymbol A^T\boldsymbol A \boldsymbol v_i=\lambda_i \boldsymbol v_i,i=1,2,\dots,n \] 接下来考虑向量\(\boldsymbol A\boldsymbol v_i,i=1,\dots,n\)，有： \[ <\boldsymbol A\boldsymbol v_i,\boldsymbol A\boldsymbol v_j>=\boldsymbol v_j^T\boldsymbol A^T\boldsymbol A\boldsymbol v_i \] 将上面两式合并，可得： \[ <\boldsymbol A\boldsymbol v_i,\boldsymbol A\boldsymbol v_j>=\boldsymbol v_j^T\boldsymbol A^T\boldsymbol A\boldsymbol v_i=\lambda_i\boldsymbol v_j^T\boldsymbol v_i \] 只有当\(1\le i=j\le r\)时，上式不为0，因此\(\boldsymbol A\boldsymbol v_1,\dots,\boldsymbol A\boldsymbol v_r\)也是一个正交向量组，且\(||\boldsymbol A\boldsymbol v_i||=\sqrt{\lambda_i}\)。

令 \[ \boldsymbol u_i=\frac{1}{\sqrt{\lambda_i}}\boldsymbol A\boldsymbol v_i=\frac{\boldsymbol A\boldsymbol v_i}{||\boldsymbol A\boldsymbol v_i||} \] 则\(\boldsymbol u_1,\dots,\boldsymbol u_r\)构成一组\(m\)维向量空间\(\mathbb R^m\)的标准正交向量组。使用施密特正交化的方法（参考施密特正交化_百度百科 (baidu.com)），可以将其扩充为\(m\)维向量空间的一组标准正交基\(\boldsymbol u_1,\dots,\boldsymbol u_r,\boldsymbol b_1,\dots,\boldsymbol b_{m-r}\)。

记\(\boldsymbol V=(\boldsymbol v_1,\dots,\boldsymbol v_n)\)，则有 \[ \begin{aligned} \boldsymbol A\boldsymbol V=&(\sqrt{\lambda_1}\boldsymbol u_1,\dots,\sqrt{\lambda_r}\boldsymbol u_r,0,\dots,0) \\ =&(\boldsymbol u_1,\dots,\boldsymbol u_r,\boldsymbol b_1,\dots,\boldsymbol b_{m-r}) \begin{pmatrix} \sqrt{\lambda_1} \\ & \ddots & & O\\ & & \sqrt{\lambda_r} \\ & O & & O\\ \end{pmatrix}_{m\times n}\\ =& \boldsymbol U\boldsymbol \Sigma \end{aligned} \] 其中\(\boldsymbol U=(\boldsymbol u_1,\dots,\boldsymbol u_r,\boldsymbol b_1,\dots,\boldsymbol b_{m-r})\)，\(\Sigma=\begin{pmatrix} \sqrt{\lambda_1} \\ & \ddots & & O\\ & & \sqrt{\lambda_r} \\ & O & & O\\ \end{pmatrix}\)。

从而可得\(\boldsymbol A=\boldsymbol U\boldsymbol \Sigma \boldsymbol V^T\)

下面考虑矩阵\(U\)的求法。由于\(\boldsymbol v_i\)为矩阵\(\boldsymbol A^T \boldsymbol A\)的特征向量，因此由\(\boldsymbol u_i=\frac{1}{\sqrt{\lambda_i}}\boldsymbol A\boldsymbol v_i\)可进一步推导得： \[ \begin{aligned} \boldsymbol A^T\boldsymbol u_i=& \frac{1}{\sqrt{\lambda_i}}\boldsymbol A^T\boldsymbol A\boldsymbol v_i \\ =& \sqrt{\lambda_i}\boldsymbol v_i \end{aligned} \] 故有： \[ <\boldsymbol A^T\boldsymbol u_i,\boldsymbol A^T\boldsymbol u_j>= \begin{cases} \lambda_i, ~~1\le i=j\le r\\ 0, ~~~~\text{else} \end{cases} \] 也就是说，\(\boldsymbol u_i\)其实是矩阵\(\boldsymbol A\boldsymbol A^T\)的特征向量。

方法

给定一个大小为\(m\times n\)的矩阵\(\boldsymbol A\)，如果\(\boldsymbol A\boldsymbol A^T=\boldsymbol U\boldsymbol \Lambda_1\boldsymbol U^T\)，\(\boldsymbol A^T\boldsymbol A=\boldsymbol V\boldsymbol \Lambda_2\boldsymbol V^T\)，则矩阵\(\boldsymbol A\)的奇异值分解为： \[ \boldsymbol A=\boldsymbol U\boldsymbol \Sigma \boldsymbol V^T \] 矩阵\(\boldsymbol U=({\boldsymbol{u}_1,\boldsymbol{u}_2,\dots,\boldsymbol{u}_m})\)的大小为\(m\times m\)，其中\(\boldsymbol{u}_i\)为列向量，它们是矩阵\(\boldsymbol A\boldsymbol A^T\)的特征向量，也被称为矩阵\(\boldsymbol A\)的左奇异向量；矩阵\(\boldsymbol V=({\boldsymbol{v}_1,\boldsymbol{v}_2,\dots,\boldsymbol{v}_n})\)的大小为\(n\times n\)，其中\(\boldsymbol{v}_i\)为列向量，它们是矩阵\(\boldsymbol A^T\boldsymbol A\)的特征向量，也被称为矩阵\(\boldsymbol A\)的右奇异向量；矩阵\(\boldsymbol \Lambda_1\)的大小为\(m\times m\)，矩阵\(\boldsymbol \Lambda_2\)的大小为\(n\times n\)，这两个矩阵对角线上的非零元素相同；矩阵\(\boldsymbol \Sigma\)的大小为\(m\times n\)，位于对角线上的元素被称为奇异值。

设矩阵\(\boldsymbol \Lambda_1\)(或者\(\boldsymbol \Lambda_2\))上的非零元素为\(\lambda_1,\lambda_2,\dots,\lambda_r\)，其中\(r\)为矩阵\(A\)的秩；设矩阵\(\boldsymbol \Sigma\)对角线上的非零元素分别为\(\sigma_1,\sigma_2,\dots,\sigma_r\)(即奇异值)，则它们满足如下关系： \[ \sigma_1=\sqrt{\lambda_1},\sigma_2=\sqrt{\lambda_2},\dots,\sigma_r=\sqrt{\lambda_r} \] 因此，奇异值分解的求解步骤可以分为下面三步：

  1. 求矩阵\(\boldsymbol A\boldsymbol A^T\)的特征值和特征向量，用单位化的特征向量构成\(\boldsymbol U\)
  2. 求矩阵\(\boldsymbol A^T\boldsymbol A\)的特征值和特征向量，用单位化的特征向量构成\(\boldsymbol V^T\)
  3. 将\(\boldsymbol A\boldsymbol A^T\)或者\(\boldsymbol A^T\boldsymbol A\)的特征值求平方根，然后构成\(\boldsymbol \Sigma\)

需要注意的是，矩阵的奇异值分解结果中，奇异值是唯一的，但是矩阵\(\boldsymbol U\)和\(\boldsymbol V\)不唯一。

几何解释

奇异值分解的几何解释：矩阵\(\boldsymbol U\)的列向量构成\(\mathbb{R}^n\)空间的一组标准正交基，表示正交坐标系的旋转或反射变换；\(\boldsymbol V\)的列向量构成\(\mathbb{R}^m\)空间的一组标准正交基，同样表示正交坐标系的旋转或反射变换；\(\boldsymbol \Sigma\)的对角元素是一组非负实数，表示\(\mathbb R^n\)中的原始正交坐标系坐标轴的缩放变换。也就是说，原始空间的一组标准正交基，经过坐标系的旋转变换\(\boldsymbol U\)，坐标轴的缩放变换\(\boldsymbol \Sigma\)，坐标系的旋转变换\(\boldsymbol V^T\)，得到了经过线性变换\(\boldsymbol A\)等价的结果。可以用下图表示：

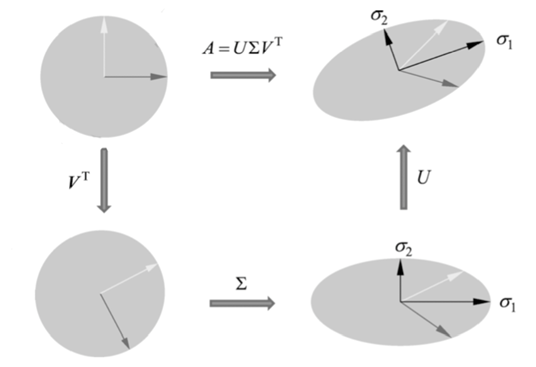
image-20210128233848022

参考

  1. The Elements of Statistical Learning
  2. 统计学习方法（第二版），李航
  3. 机器学习，周志华
  4. 奇异值分解（SVD）的定义、证明、求法（矩阵分解——3. 奇异值分解（SVD）） - 知乎 (zhihu.com)
  5. 机器学习中SVD和PCA一直没有搞的特别清楚，应该如何理解呢？ - 知乎 (zhihu.com)
  6. 主成分分析PCA算法：为什么去均值以后的高维矩阵乘以其协方差矩阵的特征向量矩阵就是“投影”？ - 知乎 (zhihu.com)