"> "> 机器学习-特征工程 | Yufei Luo's Blog

Yufei Luo's Blog

But I was so much older then, I am younger than that now.

Yufei Luo's Blog

机器学习-特征工程

发表于 更新于 分类于 ， 阅读次数：
本文字数： 18k 阅读时长 ≈ 16 分钟

概述

在机器学习任务中，数据和特征决定了机器学习的上限（例如偏差-方差分解中的噪声部分，噪声决定了机器学习任务的难度），而模型和算法只是逼近这个上限而已。而这里的数据便指的是经过特征工程得到的数据。

特征工程指的是把原始数据转变为模型的训练数据的过程，它的目的是获取更好的数据特征，使得机器学习模型可以更好地逼近学习的上限。如果使用的模型是诸如线性回归、支持向量机、决策树等统计学习模型，特征工程的作用比模型的训练更加重要，甚至当特征工程做得很好时，使用简单的模型也可以取得不错的效果。当然，对于深度学习而言，由于神经网络自身具有强大的学习能力，可以自己从数据中学到某些“特征”（当然，这些“特征”的可解释性较差），对于特征工程的要求就要相对低很多。但是，这并不意味着深度学习对特征工程没有要求，通常仍需要对数据做一些预处理。

特征工程属于一项偏实践性的工作，很难在各种机器学习的理论书籍上找到相关的介绍。本文介绍的属于一般性的常用步骤，在具体的任务中可能还需要根据任务需求或者是利用该任务相关的领域知识来帮助我们做特征工程。

注意：在本文使用到的数据中，每一行的数据代表一个样本，每一列的数据代表一个特征。

特征工程的步骤

一个完整的特征工程通常需要先对数据的基本特点做一些了解，然后对数据做一些预处理。在此基础上，再进行特征选择与降维。

在做特征工程时，经常使用到的Python函数库包括但不限于下面这些：

  • NumPy和Pandas：二者搭配使用，处理表格相关的数据，https://docs.scipy.org/doc/numpy/ ，http://pandas.pydata.org/pandas-docs/stable/
  • SciPy：科学计算相关工具，https://www.scipy.org/docs.html
  • Matplotlib、Seaborn：用于数据的可视化分析，https://matplotlib.org/contents.html ，http://seaborn.pydata.org/
  • Scikit-learn：提供了一些数据预处理相关的操作，https://scikit-learn.org/stable/index.html
1
2
3
import numpy as np
import pandas as pd
import seaborn as sns

数据初步分析

在我们做特征工程之前，通常需要首先对数据做一些初步分析，了解数据格式、数据内容、每个特征的数值分布情况、特征之间的相关性等，从而帮助我们决定接下来如何对它们进行处理。

这一部分没有固定的操作方法，需要根据数据自身的特点以及要研究的问题本身，做一些针对性的分析。可以使用的方法包括数据统计摘要（最大、最小、均值等）、可视化、统计检验等手段。在特征工程的最后一部分内容中，我们将以一个实际的例子，来说明拿到原始数据之后做一些初步分析的方法与思路。

缺失值处理

原始数据中可能会存在一些缺失值，在进行接下来的操作之前，需要先对这些缺失值进行处理。数据缺失通常可以分为三类：

  • 完全随机缺失：数据的缺失是完全随机的，不依赖于任何变量，也不影响样本的无偏性，例如家庭地址缺失。
  • 随机缺失：数据的缺失不是完全随机的，该类数据的缺失依赖于其它变量，例如财务数据缺失情况与企业的规模有关。
  • 非随机缺失：数据的缺失与变量自身的取值有关，例如高收入人群不愿意提供家庭收入数据。

对于缺失值处理的操作，通常可以使用如下几种办法：

  • 删除：如果可以确定含有缺失值的特征对于构造模型的影响很小，可以将整个特征删除。如果一个特征的缺失值数量很少，也可以删除掉含有缺失值的样本
  • 填充：对缺失值的填充大致可分为三种方法
    • 替换：使用特征的平均数、中位数、众数进行填充
    • 拟合缺失值：将缺失值对应的特征作为模型预测的目标，使用数据集中的其它特征来训练一个模型，然后基于训练好的模型去预测缺失值。
    • 虚拟变量：通过判断变量值是否有缺失值来生成一个新的二分类变量
  • 不处理：如果缺失值包含了实际含义，那么可以保留该变量。可以将缺失值填充为区别于正常值的一个默认值。

数据预处理

在对原始数据有了一些初步的了解之后，接下来需要对数据做一些预处理。由于机器学习模型对于输入数据有一些要求，因此我们对数据的处理包括对数据的取值范围进行缩放、将字符串转换为数字、对类别型变量的编码等。

特征一般分为定量特征和定性特征。定量特征指的是数值类型的变量，分为离散和连续型两种；而定性特征则指的是类别型的变量，按照这些类别是否对应于一定的等级和顺序，分为有序分类变量和无序分类变量。

需要说明的一点是，本部分内容涉及到的数据处理方法较为基础，主要用来处理表格类的数据。而实际上，许多机器学习模型，尤其是深度学习模型，可以用声音、图像、文本、视频等数据进行训练，它们的数据处理也有着各自的方法，不在本文的讨论范围之内。

定量特征无量纲化

无量纲化指的是使不同规格的数据转换到同一规格。例如一个特征的取值范围是\([0,1000]\)，而另一个特征是\([-10,10]\)，无量纲化便是将它们的取值范围移动至同一数量级。

对于树模型来说，这一操作不是必要的，因为树模型是一系列if-else的组合，在构建分支时数据的取值没有任何影响；但是对于那些需要使用数值计算进行优化的模型，例如线性回归、逻辑回归、神经网络这些需要用到梯度下降进行优化的模型，又或者是KNN、聚类这些需要计算点与点之间距离来进行优化的模型，这一步骤就尤其重要，因为数值的数量级对于模型优化方向、收敛速度，甚至是模型的最终效果都有着巨大的影响。

下面介绍几种常见的数据无量纲化的方法。

中心化

假设原始数据为\(\boldsymbol{x}\)，\(\bar{X}\)为\(\boldsymbol{x}\)的均值，则中心化的计算公式为： \[ \boldsymbol{x}'={\boldsymbol{x}-\bar{X}} \]

也就是将数据的平均值变为0。

标准化

假设原始数据为\(\boldsymbol{x}\)，\(\bar{X}\)为\(\boldsymbol{x}\)的均值，\(S\)为\(\boldsymbol{x}\)的标准差，则标准化的计算公式为： \[ \boldsymbol{x}'=\frac{\boldsymbol{x}-\bar{X}}{S} \]

标准化操作的适用条件是原始数据大致服从正态分布，标准化可以将其转换为大致服从标准正态分布。如果原始数据不服从这一条件，则会影响数据的分布规律，进而影响最终的模型训练效果。

Scikit-learn中提供了用来完成数据标准化的类StandardScaler，可以方便我们进行这一操作，下面为使用示例：

1
2
3
from sklearn.preprocessing import StandardScaler
standardscale_data=np.random.uniform(low=-2.0,high=3.0,size=(10,1))
standardscaler=StandardScaler()
1
standardscale_data
array([[ 2.62752878],
       [-0.62955258],
       [ 0.06932906],
       ...,
       [ 2.59914143],
       [ 0.61341229],
       [ 1.34356686]])
1
standardscaler.fit(standardscale_data) #传入原始数据，从中自动学得平均值与标准差
StandardScaler(copy=True, with_mean=True, with_std=True)
1
standardscaler.transform(standardscale_data) #按照学得的标准差对数据做标准化操作
array([[ 1.03975343],
       [-1.118967  ],
       [-0.65576394],
       ...,
       [ 1.02093894],
       [-0.29515778],
       [ 0.18877229]])
1
standardscaler.fit_transform(standardscale_data) #上述两步操作可以合在一起完成
array([[ 1.03975343],
       [-1.118967  ],
       [-0.65576394],
       ...,
       [ 1.02093894],
       [-0.29515778],
       [ 0.18877229]])

区间缩放法

区间缩放法的思路有很多种，比较常见的一种是利用两个最值，将原始数据缩放至\([0,1]\)区间。使用公式可以表达为： \[ \boldsymbol{x}'=\frac{\boldsymbol{x}-\min (\boldsymbol{x})}{\max (\boldsymbol{x})-\min (\boldsymbol{x})} \]

同样，Sklearn中也为这一方法提供了MinMaxScaler类，方便完成这一操作。它的使用方法与StandardScaler类似。

1
2
3
from sklearn.preprocessing import MinMaxScaler
minmaxscale_data=np.random.uniform(low=-2.0,high=3.0,size=(10,1))
minmaxscaler=MinMaxScaler()
1
minmaxscale_data
array([[ 1.76246719],
       [-0.99536845],
       [ 0.29888608],
       ...,
       [ 0.50958026],
       [ 0.35095473],
       [-0.83496883]])
1
minmaxscaler.fit_transform(minmaxscale_data)
array([[0.80278034],
       [0.08353523],
       [0.42107755],
       ...,
       [0.47602671],
       [0.43465708],
       [0.12536754]])

此外，区间缩放也可以对某个特征所有的值直接乘上或者除以一个相同的数字，从而改变它们的分布区间。

需要注意的是，StandardScaler和MinMaxScaler都是按列方向进行计算的。

归一化

归一化（又称为规范化/正则化）是依照行方向处理数据的，它的目的在于样本向量在点乘运算或者是使用核函数计算相似性时，具有统一的标准。例如规则为L2的归一化公式如下： \[ \boldsymbol{x}'=\frac{\boldsymbol{x}}{\sqrt{\sum_{i=0}^{n}x_{i}^{2}}} \]

Sklearn中也为这一方法提供了Normalizer类，方便完成这一操作。默认条件下它使用L2范数，可以在初始化的时候传入参数对其进行修改。它的使用方法如下：

1
2
3
from sklearn.preprocessing import Normalizer
normalize_data=np.random.uniform(-2.0,2.0,(3,4))
normalizer=Normalizer()
1
normalize_data
array([[-0.55817435,  1.08530818,  1.74512408, -1.46521987],
       [ 1.26433631, -1.83118327, -0.78242779, -1.67931577],
       [ 1.07275275,  1.4259531 , -0.80605024, -1.26041706]])
1
normalizer.fit_transform(normalize_data)
array([[-0.21593538,  0.41986241,  0.67511885, -0.56683508],
       [ 0.43665162, -0.63241809, -0.27021953, -0.57996907],
       [ 0.46068015,  0.61235759, -0.34614812, -0.54127023]])

定量特征离散化

定量特征离散化指的是将连续特征划分为离散的过程，将原始定量特征的一个区间一一映射到单一的值。特征被离散化之后，数据将会被简化，同时可以提升模型的鲁棒性和泛化能力；但是也在一定程度上带来了信息损失，并引入了额外的流程。

等宽和等频离散

等宽离散指的是每个分割点的划分距离一样，例如将数据序列划分为\(n\)份，那么分割点的宽度为\(w=\frac{\max-\min}{n}\)。等宽离散的方法便于计算，但是当数值之间的差距较大时，可能会出现没有数据的分箱。

等频离散理论上分割后的箱内数据量大小一致，但是当某个值出现次数较多时则可能会出现等分边界的值相等，导致同一个值被分入不同的箱内。因此需要将边界处的重复值划分到某一个分箱内，避免歧义，但是这样也导致了每个分箱的数据量不一致。

等宽和等频离散容易出现的问题是每个箱中的信息量变化不大，例如等宽分箱不太适合于分布不均匀的数据集、离群值，而等频方法则不太适合于特定值占比过多的数据集。

信息熵离散

信息熵离散是一种基于监督学习的离散办法，它实际上是使用要离散的连续型特征与样本标签去训练一个决策树模型，然后根据决策树模型的分割点来构造分箱。由于决策树在分裂时使用信息熵与信息增益作为判断准则，因此这种方法被称为信息熵离散。

这一操作可以使用sklearn提供的DecisionTreeClassifier和DecisionTreeRegressor两个类来实现，要控制分箱时的最大分箱数、每个分箱内的数据量的最小值、信息增益的阈值等条件，则可以通过向模型中传入参数来实现。例如要控制最大分箱数，则可以传入max_leaf_nodes来实现这一条件。

卡方离散

卡方离散基于卡方检验，它是一种基于合并机制的自底而上的离散化方法。它基于如下假设：如果两个相邻区间具有非常相似的类分布，那么这两个区间可以合并，否则它们应当保持分开。简单总结就是将具有最小卡方值的相邻区间合并在一起，直到满足某个停止准则。

定量特征编码

二值化

定量特征二值化的核心在于设定一个阈值，大于该阈值的赋值为1，小于等于该阈值的赋值为0，使用公式表达如下：

\[ x'= \begin{cases} 1,x>threshold \\ 0,x<threshold \end{cases} \]

Sklearn提供的Binarizer类可以使得这一操作变得简便，它的使用方法如下：

1
2
3
from sklearn.preprocessing import Binarizer
binarize_data=np.random.uniform(-2.0,2.0,(2,2))
binarizer=Binarizer(threshold=1)
1
binarize_data
array([[-0.53891812,  0.18869311],
       [ 0.5408885 ,  0.56153303]])
1
binarizer.fit_transform(binarize_data)
array([[0., 0.],
       [0., 0.]])

多值化

二值化的操作比较简单，但是对数据的分割太粗糙，无法充分利用特征。sklearn提供了KBinsDiscretizer类，可以将数据分成多个区间，然后将数值归入到所属的区间内。最终可以生成One-hot类型的编码（默认），或者是数值所属区间的编码。使用方法如下：

1
2
from sklearn.datasets import load_iris
from sklearn.preprocessing import KBinsDiscretizer
1
2
X,y=load_iris(return_X_y=True)
KBinsDiscretizer(n_bins=3).fit_transform(X)
1
2
<150x12 sparse matrix of type '<class 'numpy.float64'>'
	with 600 stored elements in Compressed Sparse Row format>

定性特征编码

独热编码

对于一些无序的分类变量，我们可以将其转换为独热编码（也叫哑编码等名称）。也就是说，假如一个特征有A、B、C三种类别，我们就将其编码为3个特征，分别对应于A、B和C。当某条数据该特征的类别为A时，就将其编码为\([1,0,0]\)，B和C就分别对应于\([0,1,0]\)和\([0,0,1]\)。

需要注意的是，这种方法不限制原始数据的类型，不仅仅是字符串型的数据，数值型的数据也可以转换为哑编码。

Sklearn提供了OneHotEncoder类可以方便地完成上述的工作，它的使用方法如下：

1
2
3
from sklearn.preprocessing import OneHotEncoder
onehotdata=np.array([['C'],['B'],['A'],['C'],['B']])
onehotencoder=OneHotEncoder(sparse=False) #默认条件下使用稀疏矩阵的压缩表示法，可以传入sparse=False来生成完整的矩阵
1
onehotdata
array([['C'],
       ['B'],
       ['A'],
       ['C'],
       ['B']], dtype='<U1')
1
onehotencoder.fit_transform(onehotdata) #在one-hot编码的时候会自动对类别型特征进行排序，然后按照排序后的顺序进行编码
array([[0., 0., 1.],
       [0., 1., 0.],
       [1., 0., 0.],
       [0., 0., 1.],
       [0., 1., 0.]])

LabelBinarizer类可以起到类似的作用，它会直接生成完整的稀疏矩阵：

1
2
3
from sklearn.preprocessing import LabelBinarizer
labelbinarizer=LabelBinarizer()
labelbinarizer.fit_transform(onehotdata)
array([[0, 0, 1],
       [0, 1, 0],
       [1, 0, 0],
       [0, 0, 1],
       [0, 1, 0]])

当特征中的类别过多时，使用one-hot编码则会使得特征维度一下子增大很多，此时可以考虑使用FeatureHasher的编码，将不同的值映射到一个指定长度的数组中。但是这种方法有碰撞的可能，而且更关键的是使得新的特征失去了本身的含义，因此需要注意其使用场景。

定性特征数值化

有时，我们想使用不同的数字来表示不同的字符串。这一步可以通过手动构造一个表示映射关系的字典类型变量来实现。此外，Sklearn也提供一个LabelEncoder类来方便我们完成这种转换操作，但是它仅限于按照字符串的排序来做数值化：

1
2
3
from sklearn.preprocessing import LabelEncoder
labeldata=np.array([['C'],['B'],['A'],['C'],['B']])
labelencoder=LabelEncoder()
1
labelencoder.fit_transform(labeldata) #在将字符串与数字对应起来的时候会自动对字符串进行排序，按照排序后的顺序转换
array([2, 1, 0, 2, 1], dtype=int64)

如果定性特征本身是有序的，则不能使用LabelEncoder，需要自己手动构造字典类型的变量进行映射操作。

WOE编码

WOE（Weight of Evidence）证据权重编码属于有监督的编码方式，它利用了标签信息，这种编码方式被广泛用于金融领域信用风险模型中。在二分类问题中，WOE的计算公式为： \[ \text{WOE}_i=\ln \frac{B_i B}{G_i G} \] 根据上式，WOE可以解释为某个特征的第\(i\)个类别中好坏样本分布比值的对数，其中\(B_i\)、\(G_i\)分别代表类别\(i\)中的坏样本，\(B\)、\(G\)分别代表坏样本和好样本的总数。

对于连续变量，则可以将其离散化之后再使用WOE的编码方式。

数学变换

有时我们需要对原始数据做一些数学变换，常见的有基于多项式、基于指数函数、基于对数函数的变换。下面的例子是用来进行多项式转换的方法：

1
2
3
from sklearn.preprocessing import PolynomialFeatures
data_transform=np.random.randn(3,1)
polyfeatures=PolynomialFeatures(degree=3) #degree代表多项式的度，即最高次项的次数，默认为2
1
data_transform
array([[-0.435727  ],
       [-0.94479211],
       [-0.16820776]])
1
polyfeatures.fit_transform(data_transform)
array([[ 1.        , -0.435727  ,  0.18985802, -0.08272627],
       [ 1.        , -0.94479211,  0.89263213, -0.8433518 ],
       [ 1.        , -0.16820776,  0.02829385, -0.00475925]])

此外，sklearn也提供了一个FunctionTransformer类，可以传入任意函数完成数据的转换。

1
2
3
from sklearn.preprocessing import FunctionTransformer
func_trans=FunctionTransformer(np.exp) #初始化时需要传入一个用于转换的函数
func_trans.fit_transform(data_transform)
array([[0.64679427],
       [0.38876038],
       [0.84517822]])

同样，sklearn也支持自定义转换器类，需要继承BaseEstimator和TransformerMixin两个类，并在类中自己定义fit和transform两个函数。自定义转换类的使用方法与sklearn自带的转换器类使用方法相同。

1
2
3
4
5
6
7
8
from sklearn.base import BaseEstimator, TransformerMixin
class MyOwnTransformer(BaseEstimator,TransformerMixin):
    def __init__(self,data=None):
        self.data=data
    def fit(self,x,y=None):
        return self
    def transform(self,x,y=None):
        return self

日期和时间特征

日期和时间特征中常见的转换方式是基于某个参考点做差得到一个定量的数值，表示经过的时间。或者是将日期和时间特征衍生为年月日、上中下旬、是否周末、是否是节假日、白天黑夜等特征。

异常值检测

异常值指的是在数据中明显与其它数值偏离的少量数值，可以通过统计检验和可视化发现。异常值产生的原因可能为偶然事件的极端表现，属于真实而正常的数据；也可能是由于系统的偶然性故障或者人为录入数据的失误所产生的结果，属于非正常数据。

异常点的检测方法有基于统计的方法、基于聚类的方法和专门的异常值检测算法等，具体可以参考本博客中的异常检测一文。

在检测出异常值之后，具体情况还需要人工判断检测结果是否准确。之后，结合实际情况决定对异常值的处理方式，可以将其删除、进行修正、或者是不处理。

特征选择

当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。无意义的特征会使得模型变得复杂，而且可能会使得模型的效果变差。此外，更少的特征也更有利于模型的解释性。

通常来说，从两个方面考虑来选择特征：

  1. 特征是否发散：如果一个特征不发散（方差接近于0），也就是说样本在这个特征上基本上没有差异，那么这个特征对于样本的区分并没有什么用。
  2. 特征与目标的相关性：与目标相关性高的特征，应当优先选择。

根据特征选择的形式，又可以将特征选择方法分为3种：

  1. 过滤法：按照发散性或者相关性对各个特征进行评分，并设定阈值或者待选择阈值的个数，然后对特征评分排序并进行选择
  2. 包装法：根据优化目标函数的表现，每次选择若干特征或者排除若干特征
  3. 嵌入法：先使用某些模型进行训练，得到各个特征的权重系数，根据系数从大到小选择特征。

在这一部分，我们使用Sklearn自带的鸢尾花（iris）数据集，对这些选择方法进行详细的讲解。

1
2
3
4
from sklearn.datasets import load_iris
orig_data=load_iris()
iris_data=orig_data.data #鸢尾花特征，包括花萼长度等4条属性
iris_target=orig_data.target #鸢尾花的类别
1
iris_data
array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       ...,
       [6.5, 3. , 5.2, 2. ],
       [6.2, 3.4, 5.4, 2.3],
       [5.9, 3. , 5.1, 1.8]])
1
iris_target
array([0, 0, 0, ..., 2, 2, 2])

过滤法

方差选择法

方差选择法先计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。Sklearn自带的VarianceThreshold类可以自动完成这一操作，下面为使用示例：

1
2
3
from sklearn.feature_selection import VarianceThreshold
varianceselector=VarianceThreshold(threshold=0.6)
varianceselector.fit_transform(iris_data)
array([[5.1, 1.4],
       [4.9, 1.4],
       [4.7, 1.3],
       ...,
       [6.5, 5.2],
       [6.2, 5.4],
       [5.9, 5.1]])

相关系数法

相关系数法先要计算数据集的各个特征对于标签的Pearson相关系数，然后根据相关系数的大小选出排名前几位的特征。相关系数的计算公式为： \[ r=\frac{\text{cov}(X,Y)}{\sqrt{\text{var}(X)\cdot \text{var}(Y)}} \]

这一方法需要使用Sklearn自带的SelectKBest或者SelectPercentile，结合NumPy的corrcoef相关系数计算函数，方法如下：

1
2
3
from sklearn.feature_selection import SelectKBest,SelectPercentile
kbest=SelectKBest(lambda x,y:np.abs(np.corrcoef(x,y,rowvar=False)[:-1,-1]),k=2)
percentile=SelectPercentile(lambda x,y:np.abs(np.corrcoef(x,y,rowvar=False)[:-1,-1]),percentile=50)
1
2
test=lambda x,y:np.abs(np.corrcoef(x,y,rowvar=False)[:-1,-1])
test(iris_data,iris_target)
array([0.78256123, 0.42665756, 0.9490347 , 0.95654733])
1
kbest.fit_transform(iris_data,iris_target)
array([[1.4, 0.2],
       [1.4, 0.2],
       [1.3, 0.2],
       ...,
       [5.2, 2. ],
       [5.4, 2.3],
       [5.1, 1.8]])
1
percentile.fit_transform(iris_data,iris_target)
array([[1.4, 0.2],
       [1.4, 0.2],
       [1.3, 0.2],
       ...,
       [5.2, 2. ],
       [5.4, 2.3],
       [5.1, 1.8]])

除了Pearson相关系数，还有基于秩的Spearman相关系数和Kendall相关系数。在Pandas的corr()函数中提供了相应的参数选项，可以计算三种不同的相关系数；SciPy的scipy.stats模块中提供了对应的三个函数接口；而Numpy只提供了Pearson相关系数的计算。

卡方检验

卡方分布（Chi-square distribution, \(\chi^2\)-distribution）是概率统计中一种常用的概率分布。如果\(k\)个独立的随机变量\(Z_1,Z_2,\dots,Z_k\)符合标准正态分布\(N(0,1)\)，那么这\(k\)个随机变量的平方和\(X=\sum_{i=1}^{k}Z_{i}^{2}\)服从自由度为\(k\)的卡方分布，记作\(X\sim \chi ^2(k)\)。卡方分布的期望\(E(\chi ^2)=n\)，方差\(D(\chi ^2)=2n\)。

卡方检验是以卡方分布为基础的一种假设检验方法，主要用于类别型变量。其基本思想是根据样本数据推断总体的分布与期望分布是否有显著性差异，或者推断两个类别型变量是否相关或者独立。

如果我们使用卡方检验筛选特征时，我们对数据的某个特征做出假设为\(H_0\)：该特征与数据的标签相互独立。我们假设\(H_0\)成立，计算出\(\chi^2\)的值，它表示实际观察值与假设成立时的理论值之间的偏离程度。根据\(\chi^2\)分布、\(\chi^2\)统计量以及自由度，可以确定在\(H_0\)成立的情况下获得当前统计量以及更极端情况的概率\(p\)。如果\(p\)很小，说明观察值与理论值的偏离程度大，应该拒绝原假设，否则不能拒绝原假设。\(\chi^2\)的计算公式为：\(\chi^2=\sum \frac{(A-T)^2}{T}\)，其中\(A\)为实际值，\(T\)为假设\(H_0\)成立时的理论值。关于卡方检验的实际例子可以参考文章：https://blog.csdn.net/ludan_xia/article/details/81737669。

在使用卡方检验筛选特征时，我们需要计算每个特征相对于数据标签的卡方值。一般来说，卡方值越大，说明关联越强，特征越需要保留。使用Sklearn中的SelectKBest和chi2两个类，便可以结合卡方检验来选取特征，操作如下：

1
2
3
from sklearn.feature_selection import SelectKBest,chi2
chi2select=SelectKBest(chi2,k=2)
chi2select.fit_transform(iris_data,iris_target)
array([[1.4, 0.2],
       [1.4, 0.2],
       [1.3, 0.2],
       ...,
       [5.2, 2. ],
       [5.4, 2.3],
       [5.1, 1.8]])

包装法

递归特征消除法

递归特征消除法使用一个基模型来进行多轮训练，每轮训练之后消除若干权值系数的特征，再基于新的特征集进行下一轮训练。如此重复，根据这些模型的表现来决定最终使用哪些特征。

Sklearn提供了RFE（Recursive Feature Elimination）类来完成这一操作，它的使用方法如下：

1
2
3
4
5
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

rfe_selector=RFE(LogisticRegression(),n_features_to_select=2)
rfe_selector.fit_transform(iris_data,iris_target)
array([[1.4, 0.2],
       [1.4, 0.2],
       [1.3, 0.2],
       ...,
       [5.2, 2. ],
       [5.4, 2.3],
       [5.1, 1.8]])

嵌入法

基于惩罚项的特征选择法

使用带有惩罚项的基模型，除了筛选出特征之外同时也进行了降维。下面的例子是使用SelectFromModel类结合带有L2惩罚项的逻辑回归模型来选择特征：

1
2
3
4
5
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression

model_selector_penal=SelectFromModel(LogisticRegression(penalty='l2',C=0.1))
model_selector_penal.fit_transform(iris_data,iris_target)
array([[1.4, 0.2],
       [1.4, 0.2],
       [1.3, 0.2],
       ...,
       [5.2, 2. ],
       [5.4, 2.3],
       [5.1, 1.8]])

基于树模型的特征选择法

树模型中的梯度提升树和随机森林等模型可以根据每个非叶结点上用于分支的特征以及它们的得分，来计算每个特征的重要性，因此这些模型也可以用于特征选择。使用SelectFromModel类结合随机森林模型选择特征的代码如下：

1
2
3
4
5
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier

model_selector_tree=SelectFromModel(RandomForestClassifier())
model_selector_tree.fit_transform(iris_data,iris_target)
array([[1.4, 0.2],
       [1.4, 0.2],
       [1.3, 0.2],
       ...,
       [5.2, 2. ],
       [5.4, 2.3],
       [5.1, 1.8]])

降维

维度灾难

在特征选择完成之后，可能特征矩阵仍然较大。这不仅会导致计算量大，训练时间长，而且更重要的是会造成计算上的“维度灾难”(The curse of dimensionality)。下面为两个维度灾难的例子。

第一个例子与高维空间中的数据采样有关。为了简便，我们假设数据在一个\(p\)维的单位长度超立方体中均匀分布。如果以某个点为中心，构造一个小的超立方体，要求其中包含的数据点占总数据的比例为\(r\)，那么这个超立方体的边长应当为\(e_{p}(r)=r^{1/p}\)。当\(p=10\)时，如果取\(r=0.01\)，\(e_{10}(0.01)\approx 0.63\)；而当\(p=5\)时，同样取\(r=0.01\)，此时\(e_{5}(0.01)\approx 0.40\)。也就是说，在10维的超立方体中，当我们仅仅需要1%的数据时，就需要对每个特征覆盖63%的取值范围。而在5维的超立方体中，如果取1%的数据，我们只需要对每个特征覆盖40%的取值范围。

另一个例子与高维空间中的距离计算有关。考虑一个单位长度超立方体的对角线长度，当维度\(p=5\)时，这个距离是\(\sqrt{5}\)；而当维度\(p=20\)时，这个距离已经变成了\(2\sqrt{5}\)。

上面两个例子说明了，高维空间中的两个看似近邻的点，它们的实际距离可能已经不再“近邻”。或者说，高维空间中的数据会变得“稀疏”。因此，对于高维数据，我们仍需要采取一些办法来进行降维，从而减小维度过高造成的负面影响。

主成分分析法

原理

主成分分析(Principle Components Analysis, PCA)属于无监督学习算法，它的想法是用一个\(q\)维的数据去尽可能地近似表达原本\(p(p>q)\)维的数据。

PCA的主要思想是从最大方差的角度去考虑，它的出发点是在数据降维之后，能够在降维后的特征上保持尽可能大的方差。这样在降维后的数据上，能够使得数据点尽可能地分散。

下图是PCA将原始数据从三维降到二维的示意图：

PCA

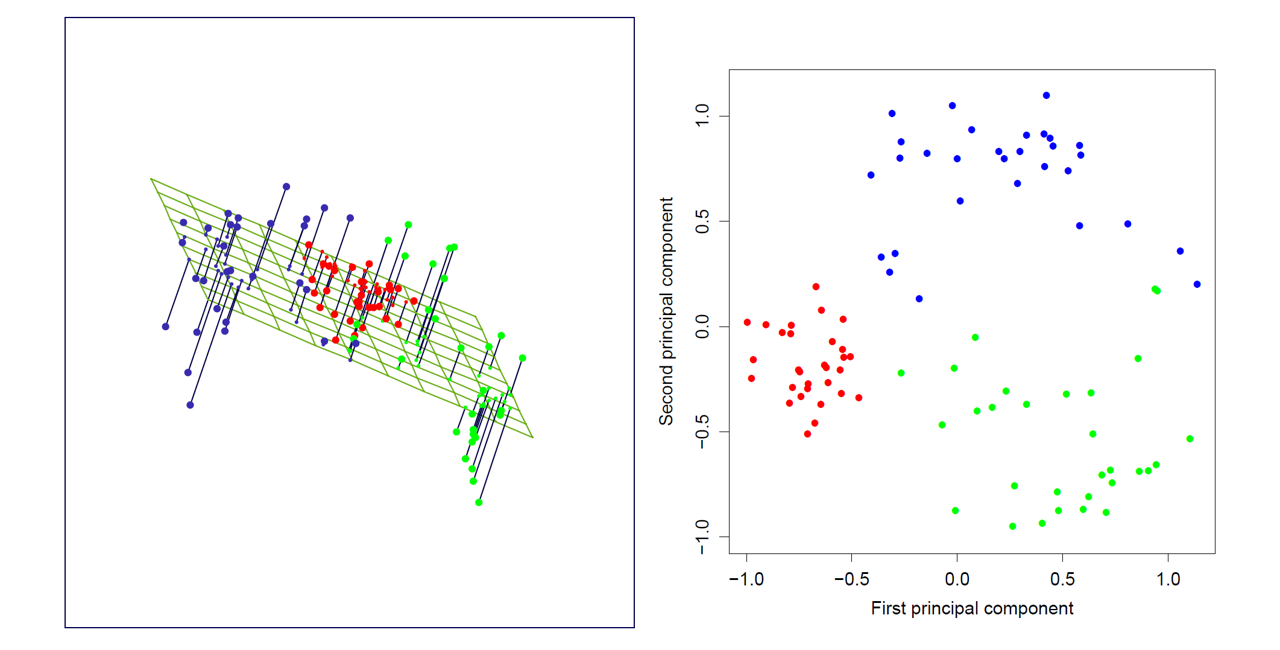
实现

Sklearn中的PCA类可以方便地完成主成分分析的操作，它的使用示例如下：

1
2
3
from sklearn.decomposition import PCA
pca=PCA(n_components=2) #n_components可以为整数，代表选择保留的主成分个数；也可以传入一个0-1之间的浮点数，表示所希望达到的方差贡献率，此时会自动选取特征值靠前的若干个主成分，直到方差贡献率刚好满足条件。
pca.fit_transform(iris_data)
array([[-2.68412563,  0.31939725],
       [-2.71414169, -0.17700123],
       [-2.88899057, -0.14494943],
       ...,
       [ 1.76434572,  0.07885885],
       [ 1.90094161,  0.11662796],
       [ 1.39018886, -0.28266094]])

当数据量或者是特征数目很大的时候，无论是对特征矩阵计算协方差还是做奇异值分解，所需的内存以及计算量都很大。为了解决这一问题，有两种办法。

第一种办法是使用增量PCA的办法，这种办法允许我们将数据集分批输入，每次只输入一个小批量。这种办法对大型训练集很有用，而且可以用于在线学习的情景。Sklearn提供了IncrementalPCA类，用来做增量PCA，它的使用方法如下：

1
2
3
4
5
6
from sklearn.decomposition import IncrementalPCA
n_batches=20
inc_pca=IncrementalPCA(n_components=2)
for X_batch in np.array_split(iris_data,n_batches):
    inc_pca.partial_fit(X_batch)
inc_pca.transform(X_batch)
array([[ 2.56282819,  0.28217892],
       [ 2.41842883,  0.31240878],
       [ 1.94423122,  0.18790271],
       ...,
       [ 1.76430561,  0.07992847],
       [ 1.90016469,  0.12989783],
       [ 1.38953673, -0.2751793 ]])

另一种计算PCA的方法为随机PCA。它是一种随机算法，可以快速地找到前若干个主成分的近似值。这种算法的时间复杂度与选取的主成分个数有关，而不是与特征个数有关。因此当选取的主成分个数远小于特征个数时，它比普通的PCA算法快得多。

如果要使用随机PCA，则需要在PCA类初始化的时候传入参数svd_solver='randomized'：

1
2
3
from sklearn.decomposition import PCA
rnd_pca=PCA(n_components=2,svd_solver='randomized')
rnd_pca.fit_transform(iris_data)
array([[-2.68412563,  0.31939725],
       [-2.71414169, -0.17700123],
       [-2.88899057, -0.14494943],
       ...,
       [ 1.76434572,  0.07885885],
       [ 1.90094161,  0.11662796],
       [ 1.39018886, -0.28266094]])

线性判别分析法

原理

不同于PCA，线性判别分析(Linear Discrimination Analysis, LDA)是一种监督学习算法。它的基本思想是设法将训练样本投影到一条直线上，使得同类样本的投影点尽可能地接近、异类样例的投影点尽可能地远离。而在对新样本进行分类时，将其投影到同样的直线上，再根据投影点的位置来确定新样本的类别。下图为LDA在二维空间内的一个示例：

LDA

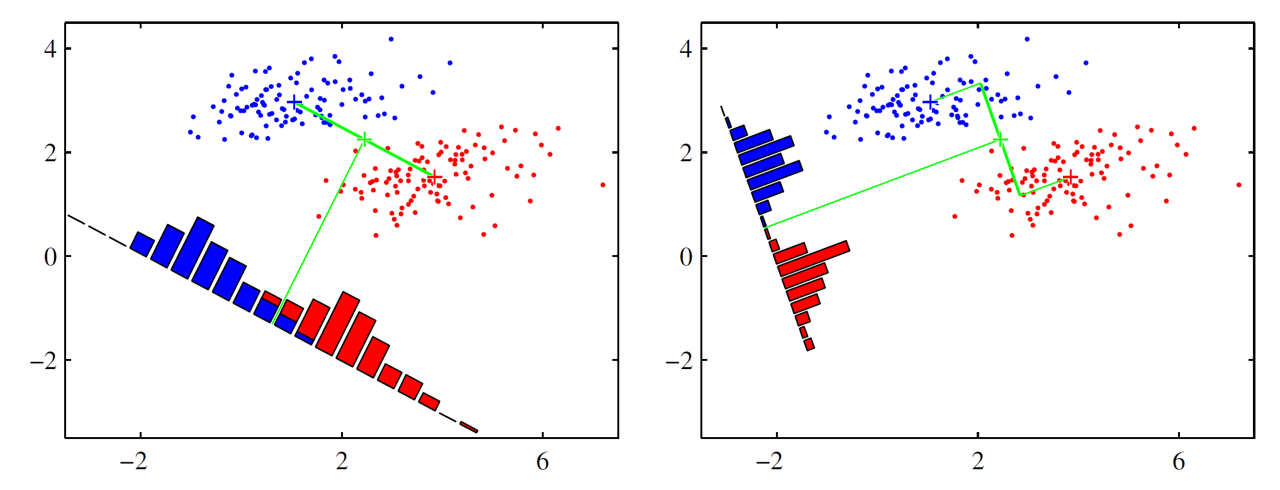
实现

Sklearn中提供了LinearDiscriminantAnalysis类，可以用来计算LDA，使用方法如下所示：

1
2
3
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda=LinearDiscriminantAnalysis(n_components=2)
lda.fit_transform(iris_data,iris_target)
array([[-8.06179978,  0.30042062],
       [-7.12868772, -0.78666043],
       [-7.48982797, -0.26538449],
       ...,
       [ 4.9677409 ,  0.82114055],
       [ 5.88614539,  2.34509051],
       [ 4.68315426,  0.33203381]])

流水线操作

由于特征工程通常需要包含很多步的操作，如果具有多份相同格式的数据需要使用相同的办法进行处理，便可以借助sklearn提供的流水线操作函数来方便操作。sklearn提供的Pipeline类可以定义一个流水线操作，初始化的时候需要传入一个list作为参数，其中的每个元素都是一个(name, function)的二元tuple。下面示例为一个生成多项式变量之后再标准化的流水线操作：

1
2
3
4
5
6
from sklearn.pipeline import Pipeline
polynomial_feature_gen=Pipeline((
    ('poly_features',PolynomialFeatures()),
    ('scaler',StandardScaler()),
))
polynomial_feature_gen.fit_transform(iris_data)
array([[ 0.        , -0.90068117,  1.01900435, ..., -1.21241227,
        -1.17404107, -1.08301943],
       [ 0.        , -1.14301691, -0.13197948, ..., -1.21241227,
        -1.17404107, -1.08301943],
       [ 0.        , -1.38535265,  0.32841405, ..., -1.23386659,
        -1.17829941, -1.08301943],
       ...,
       [ 0.        ,  0.79566902, -0.13197948, ...,  0.78045488,
         0.98068362,  1.08791683],
       [ 0.        ,  0.4321654 ,  0.78880759, ...,  0.94891095,
         1.41077689,  1.79511576],
       [ 0.        ,  0.06866179, -0.13197948, ...,  0.69861065,
         0.72092432,  0.67127249]])

参考

  1. https://www.cnblogs.com/wxquare/p/5484636.html
  2. https://www.zhihu.com/question/29316149
  3. Hands-on Machine Learning with Scikit-learn and TensorFlow
  4. 机器学习：软件工程方法与实现
  5. The Elements of Statistical Learning
  6. 机器学习，周志华
  7. https://blog.csdn.net/ludan_xia/article/details/81737669