概述

EM算法是一种迭代算法，它用于含有隐变量的概率模型参数的极大似然估计（或极大后验概率估计）。EM算法的每次迭代由两步组成：E（Expectation）步求期望，M（Maximization）步求极大值，所以这一算法也被称为期望极大算法。

对于EM算法的定性理解可以用这样的一个例子。假设现在有两个硬币A和B，我们要估计掷硬币时它们正面朝上的概率。如果我们知道每次扔出的硬币是A还是B，那么就可以直接用最大似然方法去估计；但是如果我们不知道每次扔出的是哪一枚硬币呢（即隐变量为每次实验扔出的是哪一个硬币）？此时便可以用EM算法去估计它们正面朝上的概率。如下图所示：

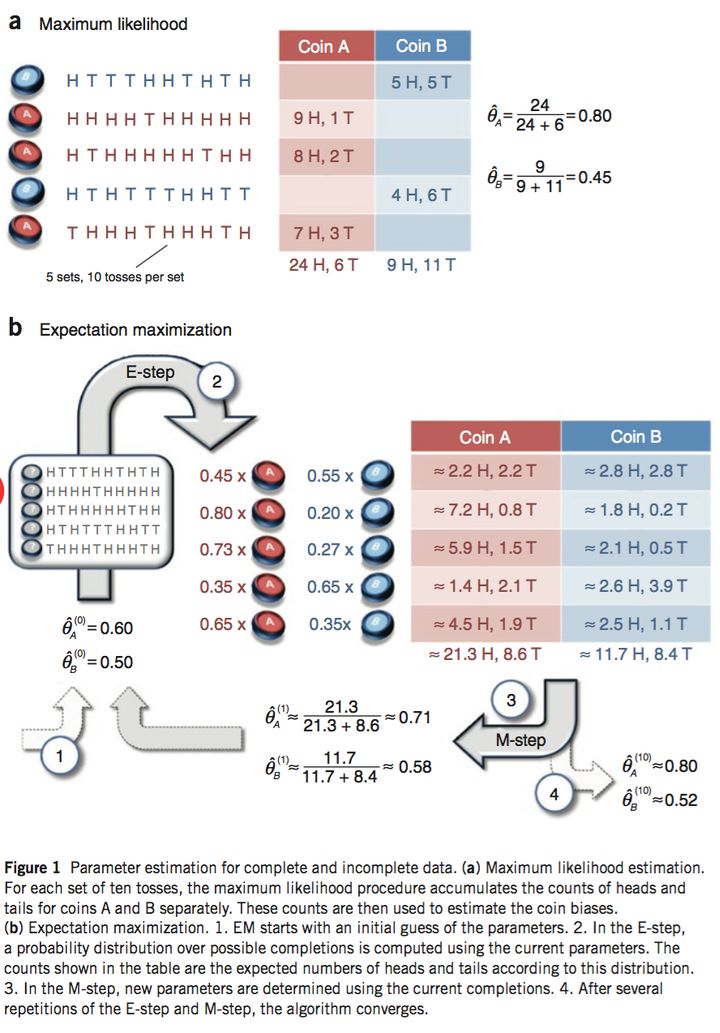
算法的数学表述如下：

输入：观测变量数据$Y$，隐变量数据$Z$，联合分布$P(Y,Z|\theta)$，条件分布$P(Z|Y,\theta)$

输出：模型参数$\theta$

算法步骤：

选择参数的初值$\theta^{(0)}$，开始迭代。参数的初值可以任意选择，但是EM算法是对初值敏感的算法，不同的初值对于算法的迭代结果是有影响的。
E步：记$\theta^{(i)}$为第$i$次迭代参数$\theta$的估计值，在第$i+1$次迭代的E步，计算 \[ \begin{aligned} Q(\theta,\theta^{(i)})=&E_Z[\log P(Y,Z|\theta)|Y,\theta^{(i)}] \\ =&\sum_{Z}\log P(Y,Z|\theta)P(Z|Y,\theta^{(i)}) \end{aligned} \] 其中，函数$Q(\theta,\theta^{(i)})$是EM算法的核心，被称为Q函数。它指的是完全数据的对数似然函数$\log P(Y,Z|\theta)$关于在给定观测数据$Y$和当前参数$\theta^{(i)}$下对未观测数据$Z$的条件概率分布$P(Z|Y,\theta^{(i)})$的期望。
M步：求使得$Q(\theta,\theta^{(i)})$极大化的$\theta$，确定第$i+1$次迭代参数的估计值$\theta^{(i+1)}=\text{arg}\max_{\theta} Q(\theta,\theta^{(i)})$。
重复步骤2和3，直到收敛。收敛的判断通常是给定一个较小的正数$\epsilon$，如果满足 \[ ||\theta^{(i+1)}-\theta^{(i)}||<\epsilon~~or~~||Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)})||<\epsilon \] 则停止迭代。

引入隐变量的目的是为了方便问题的求解。对于使用EM算法求解的问题来说，如果直接优化似然函数很困难，但是如果引入隐变量则会使得问题更容易求解。这种方法也被称为数据增强（Data augmentation）。

算法推导与证明

算法导出

对于一个含有隐变量（我们记作Z）的概率模型，我们的目标是极大化观测数据Y（不完全数据）关于参数$\theta$的对数似然函数，即最大化 \[ \begin{aligned} L(\theta)=&\log P(Y|\theta) \\ =&\log \sum_{Z}P(Y,Z|\theta)) \\ =&\log \left(\sum_{Z}P(Y|Z,\theta)P(Z|\theta)\right) \end{aligned} \] EM算法的思想是通过逐步迭代来近似极大化$L(\theta)$，假设第$i$次迭代之后$\theta$的估计值是$\theta^{(i)}$，我们希望新的估计值$\theta$能够使得$L(\theta)$增加，即$L(\theta)>L(\theta^{(i)})$，并逐步达到极大值。

我们考虑二者的差： \[ L(\theta)-L(\theta^{(i)})=\log \left(\sum_{Z}P(Y|Z,\theta)P(Z|\theta)\right)-\log P(Y|\theta^{(i)}) \] 使用Jenson不等式我们可以得到它的下界： \[ \begin{aligned} L(\theta)-L(\theta^{(i)})=&\log \left(\sum_{Z}P(Z|Y,\theta^{(i)})\frac{\sum_{Z}P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})}\right)-\log P(Y|\theta^{(i)}) \\ \ge &\sum_{Z}P(Z|Y,\theta^{(i)})\log \frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})}-\log P(Y|\theta^{(i)}) \\ =& \sum_{Z}P(Z|Y,\theta^{(i)})\log \frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} \end{aligned} \] 令 \[ B(\theta,\theta^{(i)})=L(\theta^{(i)})+\sum_{Z}P(Z|Y,\theta^{(i)})\log \frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} \] 则有$L(\theta)\ge B(\theta,\theta^{(i)})$成立，也就是说函数$B(\theta,\theta^{(i)})$是$L(\theta)$的一个下界，而且$L(\theta^{(i)})=B(\theta^{(i)},\theta^{(i)})$成立。因此，任何可以使得$B(\theta,\theta^{(i)})$增大的$\theta$，也都可以使得$L(\theta)$增大。为了使得$L(\theta)$有尽可能大的增长，在迭代过程中$\theta^{(i+1)}$一般选择能够使得$B(\theta,\theta^{(i)})$达到极大的值，即 \[ \begin{aligned} \theta^{(i+1)}=&\text{arg}\max_{\theta} B(\theta,\theta^{(i)}) \\ =& \text{arg}\max_{\theta}\left(L(\theta^{(i)})+\sum_{Z}P(Z|Y,\theta^{(i)})\log \frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})}\right) \\ =& \text{arg}\max_{\theta}\left(\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Y|Z,\theta)P(Z|\theta)\right) \\ =& \text{arg}\max_{\theta}\left(\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Y,Z|\theta)\right) \\ \end{aligned} \] 我们记 \[ Q(\theta,\theta^{(i)})=\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Y,Z|\theta) \] 那么$\theta^{(i+1)}=\text{arg}\max_{\theta} Q(\theta,\theta^{(i)})$。这相当于是EM算法的一次迭代过程，即求Q函数（E步）并最大化（M步）。

回顾：此处提到的Q函数与上文所述的Q函数相同，指的是完全数据的对数似然函数$\log P(Y,Z|\theta)$关于在给定观测数据$Y$和当前参数$\theta^{(i)}$下对未观测数据$Z$的条件概率分布$P(Z|Y,\theta^{(i)})$的期望，即$E[\log P(Y,Z|\theta)|Y,\theta^{(i)}]$。

收敛性证明

接下来我们证明这一算法的收敛性。设$P(Y|\theta)$是观测数据的似然函数，$\theta^{(i)}(i=1,2,\dots)$是EM算法得到的参数估计序列，要证明算法收敛，我们需要证明参数估计序列对应的似然函数序列$P(Y|\theta^{(i)})$是单调递增的。

根据条件概率公式，有： \[ P(Y|\theta)=\frac{P(Y,Z|\theta)}{P(Z|Y,\theta)} \] 对上式取对数，可得： \[ \log P(Y|\theta)=\log {P(Y,Z|\theta)}- \log {P(Z|Y,\theta)} \] 令$H(\theta,\theta^{(i)})=\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Z|Y,\theta)$，并将$Q(\theta,\theta^{(i)})$的表达式代入上式，可得： \[ \log P(Y|\theta)=Q(\theta,\theta^{(i)})-H(\theta,\theta^{(i)}) \] 在上式中分别取$\theta$为$\theta^{(i)}$和$\theta^{(i+1)}$，并将结果相减，可得： \[ \log P(Y|\theta^{(i+1)})-\log P(Y|\theta^{(i)})=\left[Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)})\right]-\left[H(\theta^{(i+1)},\theta^{(i)})-H(\theta^{(i)},\theta^{(i)})\right] \] 在上式中，由于$\theta^{(i+1)}$是使得$Q(\theta,\theta^{(i)})$取极大值的一组参数，因此$Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)})\ge 0$一定成立；而对于$H(\theta^{(i+1)},\theta^{(i)})-H(\theta^{(i)},\theta^{(i)})$这一项而言，有下面的结论（同样使用到了Jenson不等式）： \[ \begin{aligned} H(\theta^{(i+1)},\theta^{(i)})-H(\theta^{(i)},\theta^{(i)})=&\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Z|Y,\theta^{(i+1)})-\sum_{Z}P(Z|Y,\theta^{(i)})\log P(Z|Y,\theta^{(i)}) \\ =&\sum_{Z} \left(P(Z|Y,\theta^{(i)})\log \frac{P(Z|Y,\theta^{(i+1)})}{P(Z|Y,\theta^{(i)})} \right) \\ \le & \sum_{Z}\log \left(P(Z|Y,\theta^{(i)})\frac{P(Z|Y,\theta^{(i+1)})}{P(Z|Y,\theta^{(i)})} \right)\\ =& 0 \end{aligned} \] 因此，$\log P(Y|\theta^{(i+1)})-\log P(Y|\theta^{(i)})\ge 0$对于序列中的任意一组$\theta^{(i)}$和$\theta^{(i+1)}$都成立。由此我们证明得出似然函数序列$P(Y|\theta^{(i)})$是单调递增的。

同时，如果$P(Y|\theta)$有上界，那么由$\log(x)$的单调性以及$P(Y|\theta)$的有界性可得，$L(\theta^{(i)})=\log P(Y|\theta^{(i)})$会收敛至某一值$L^*$；在函数$Q(\theta,\theta^{(i)})$与$L(\theta)$满足一定条件下，由EM算法得到的参数估计序列$\theta^{(i)}$的收敛值$\theta^*$是$L(\theta)$的稳定点（这一结论在此不做证明）。需要注意的是，这一结论也只能保证参数估计序列收敛到对数似然序列的稳定点，不能保证收敛到极大值点。

因此在应用中，常常选取几个不同的初值进行迭代，然后对得到的几组不同的参数进行比较，从中选出更好的那组。

推广：GEM算法

如果我们将隐变量改为隐分布，则可以得到广义的EM算法（GEM算法）。 \[ \begin{aligned} L(\theta)=&\log P(Y|\theta) \\ =&\log \int P(Y,Z|\theta)dZ \\ =&\log \int q(Z)\frac{P(Y,Z|\theta)}{q(Z)}dZ \\ \ge & q(Z)\int \log\frac{P(Y,Z|\theta)}{q(Z)}dZ \\ =& \int q(Z)\log P(Y,Z|\theta)dZ - \int q(Z)\log q(Z)dZ \\ \end{aligned} \] 我们令$F(q,\theta)=\int q(Z)\log P(Y,Z|\theta)dZ - \int q(Z)\log q(Z)dZ$，此时EM算法的一次迭代则是由$F$函数的极大-极大算法实现：E步是在固定$\theta^{(i)}$的前提下，求$q^{(i+1)}(Z)$使得F函数极大化；M步是在固定$q^{(i+1)}(Z)$的前提下，求$\theta^{(i+1)}$使得F函数极大化。

上述GEM算法的优化过程如下图所示。E步相当于是优化隐变量的分布，而M步则是基于当前的隐变量分布来优化模型参数。

应用：高斯混合模型

概述

高斯混合模型（Gaussian Mixture Model）是指$K$个独立的高斯模型组成的如下形式的概率分布模型： \[ P(y|\theta)=\sum_{k=1}^{K}\alpha_k\phi(y|\theta_k) \] 其中$\alpha_k$为混合系数，满足$\alpha_k\ge 0$和$\sum_{k=1}^{K}\alpha_k=1$，代表第$k$个模型的权重；$\phi(y|\theta_k)$是高斯分布密度，$\theta_k=(\mu_k,\sigma_k^2)$， \[ \phi(y|\theta_k)=\frac{1}{\sqrt{2\pi}\sigma_k}\exp\left(-\frac{(y-\mu_k)^2}{2\sigma_k^2}\right) \] 代表第$k$个分模型，$k=1,2,\dots,K$。

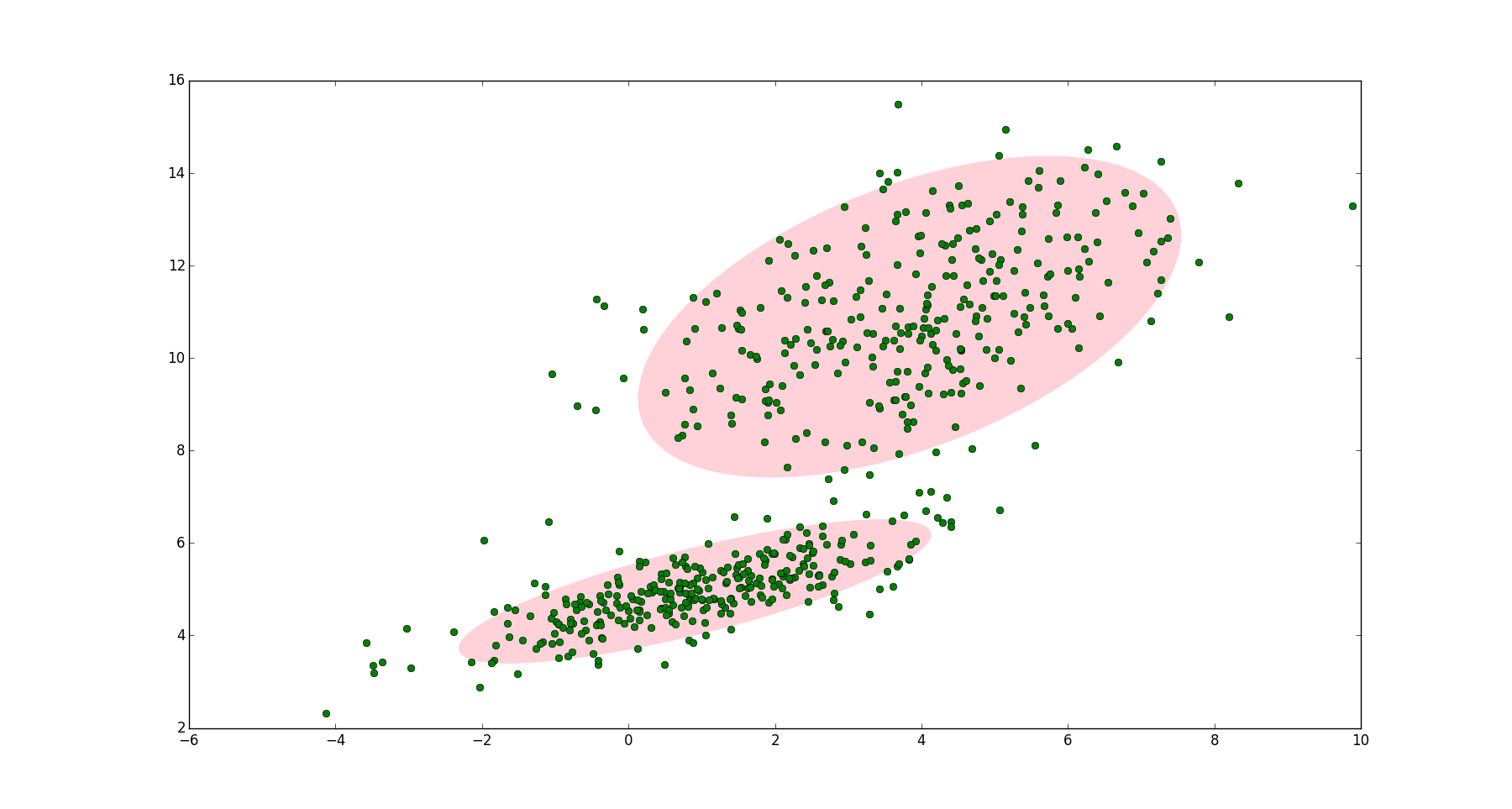
注意：

一般的混合模型可以用任意的概率分布密度来替代其中的高斯分布密度，其参数求解过程与高斯混合模型类似。

出于推导过程的简单起见，我们以一元高斯分布为例进行推导。在实际使用中，高斯分布可以是多元的。

参数求解

我们假设观测数据$y_1,y_2,\dots,y_N$是由如下的高斯混合模型生成： \[ P(y|\theta)=\sum_{k=1}^{K}\alpha_k\phi(y|\theta_k) \] 其中$\theta=(\alpha_1,\alpha_2,\dots,\alpha_K;\theta_1,\theta_2,\dots,\theta_K)$。如果直接求解这一模型的参数比较困难，因此我们引入隐变量，使用EM算法估计模型的参数$\theta$。求解步骤如下：

构造隐变量，写出完全数据的对数似然函数

我们设想观测数据$y_j,j=1,2,\dots,n$是这样产生的：首先依照概率$\alpha_k$选择第$k$个高斯分布分模型$\phi(y|\theta_k)$；然后依照第$k$个分模型的概率分布$\phi(y|\theta_k)$生成观测数据$y_j$。

此时，观测数据$y_j,j=1,2,\dots,n$是已知的；而反映观测数据$y_j$来自于第$k$个分模型是未知的，为此我们定义隐变量$\gamma_{jk}$，它的取值规则如下： \[ \gamma_{jk}= \begin{cases} 1, ~~\text{第$j$个观测数据来自于第$k$个分模型}\\ 0, ~~\text{其它} \end{cases} \] 在定义隐变量之后，我们可得到如下的完全数据： \[ (y_j,\gamma_{j1},\gamma_{j2},\dots,\gamma_{jK}),~~j=1,2,\dots,N \] 于是我们便可写出完全数据的似然函数： \[ \begin{aligned} P(y,\gamma|\theta)=&\prod_{j=1}^{N}P(y_j,\gamma_{j1},\gamma_{j2},\dots,\gamma_{jK}|\theta) \\ =&\prod_{k=1}^{K}\prod_{j=1}^{N}[\alpha_k\phi(y_j|\theta_k)]^{\gamma_{jk}} \\ =&\prod_{k=1}^{K}\prod_{j=1}^{N}\left[\alpha_k\frac{1}{\sqrt{2\pi}\sigma_k}\exp\left(-\frac{(y-\mu_k)^2}{2\sigma_k^2}\right)\right]^{\gamma_{jk}} \end{aligned} \] 那么完全数据的对数似然函数为： \[ \log P(y,\gamma|\theta)=\sum_{k=1}^{K} \left\{ \sum_{j=1}^{N}\gamma_{jk}\log\alpha_k + \sum_{j=1}^{N}\gamma_{jk} \left[ \log \frac{1}{\sqrt{2\pi}}-\log\sigma_k-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2 \right] \right\} \]
EM算法的E步：确定Q函数

根据上一步求出的对数似然函数，我们可得： \[ \begin{aligned} Q(\theta,\theta^{(i)})=&E[\log P(y,\gamma|\theta)|y,\theta^{(i)}]\\ =&\sum_{k=1}^{K}\left\{\sum_{j=1}^{N} E(\gamma_{jk}) \log \alpha_k+\sum_{j=1}^{N} E(\gamma_{jk}) \left[ \log \frac{1}{\sqrt{2\pi}}-\log\sigma_k-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2 \right] \right\} \\ \end{aligned} \] 在上式中，我们需要计算$E(\gamma_{jk})$的值，我们将其记为$\hat{\gamma}_{jk}$，它的计算公式如下： \[ \begin{aligned} \hat{\gamma}_{jk}=&E(\gamma_{jk}|y_j,\theta)=P(\gamma_{jk}=1|y_j,\theta) \\ =&\frac{P(\gamma_{jk}=1,y_j|\theta)}{\sum_{k=1}^{K}P(\gamma_{jk}=1,y_j|\theta)} \\ =&\frac{P(y_j|\gamma_{jk}=1,\theta)P(\gamma_{jk}=1|\theta)}{\sum_{k=1}^{K}P(y_j|\gamma_{jk}=1,\theta)P(\gamma_{jk}=1|\theta)} \\ =&\frac{\alpha_k\phi(y_j|\theta_k)}{\sum_{k=1}^{K}\alpha_k\phi(y_j|\theta_k)} \end{aligned} \]

备注：在$\hat{\gamma}_{jk}$表达式的推导过程中，$P(y_j|\gamma_{jk}=1,\theta)$代表数据$y_j$产生自第$k$个高斯模型时，模型产生这一数据的概率大小，因此它对应于$\phi(y|\theta_k)$；$P(\gamma_{jk}=1|\theta)$代表第$k$个模型被选中的概率，因此它对应于$\alpha_k$这一项。

$\hat{\gamma}_{jk}$指的是在当前的模型参数下，第$j$个观测数据来自于第$k$个分模型的概率，称为分模型$k$对观测数据的响应度。将$E(\gamma_{jk})$，即$\hat{\gamma}_{jk}$，代入到Q函数中，可得： \[ Q(\theta,\theta^{(i)})=\sum_{k=1}^{K}\left\{\sum_{j=1}^{N} \hat{\gamma}_{jk} \log \alpha_k+\sum_{j=1}^{N} \hat{\gamma}_{jk} \left[ \log \frac{1}{\sqrt{2\pi}}-\log\sigma_k-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2 \right] \right\} \\ \]
EM算法的M步

M步便是要求$\theta^{(i+1)}=\text{arg} \max_{\theta} Q(\theta,\theta^{(i)})$。我们将$\theta^{(i+1)}$的各个参数分别表示为$\hat{\mu}_k,\hat{\sigma}_k,\hat{\alpha}_k$，$k=1,2,\dots,K$。要计算$\hat{\mu}_k,\hat{\sigma}_k$的值，只需要对$Q(\theta,\theta^{(i)})$求$\mu_k,\sigma_k$的偏导数并令其为0即可；而计算$\hat{\alpha}_k$，由于条件$\sum_{k=1}^{K}\alpha_k=1$的限制，需要先使用拉格朗日乘子法构造关于$Q(\theta,\theta^{(i)})$的拉格朗日函数，然后求$\alpha_k$的偏导数并令其为0。它们的计算结果如下（此处省略推导过程）： \[ \begin{aligned} \hat{\mu}_k&=\frac{\sum_{j=1}^N \hat{\gamma}_{jk}y_j}{\sum_{j=1}^N \hat{\gamma}_{jk}} \\ \hat{\sigma}_k^2&=\frac{\sum_{j=1}^N \hat{\gamma}_{jk}(y_j-\mu_k)^2}{\sum_{j=1}^N \hat{\gamma}_{jk}} \\ \hat{\alpha}_k&=\frac{\sum_{j=1}^N \hat{\gamma}_{jk}}{N} \end{aligned} \]

在使用EM算法求解高斯混合模型的参数时，需要先选择一组初始值，然后再不断地迭代求解，直到对数似然函数值不再有明显的变化。

代码示例

我们使用Sklearn自带的make_blobs函数来人工生成数据，来演示如何使用sklearn中的高斯混合模型。给定簇的数量以及每个簇内的元素个数，make_blobs函数会按照多元高斯分布为每一个簇生成数据。其中每个簇的中心可以自己定义，也可以随机生成；每个簇的标准差也可以自己定义或者是全部使用相同的标准差。

我们使用随机生成的簇中心以及标准差来生成6个簇，然后对这些簇使用高斯混合模型。

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib
from matplotlib.colors import LogNorm
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split

x,y=make_blobs(
    n_samples=[100,180,200,150,120,80], 
    n_features=2,
    centers=(np.random.rand(6,2)-0.5)*20,
    cluster_std=(np.random.rand(6,1)+1)
)

1	from sklearn.mixture import GaussianMixture

GaussianMixture类在初始化时的关键参数有：

n_conponents：最终的混合模型中由有多少个高斯分布模型混合而成。默认值为1
covariance_type：不同的高斯分布模型之间协方差的关系。包括'full'（默认值）：所有的模型有自己独立的协方差矩阵；'tied'：所有模型使用同一个协方差矩阵；'diag'：每个模型有自己的对角协方差矩阵，即特征之间独立；'spherical'：每个模型有自己的方差值，即每个特征都使用相同的方差。
n_init：同时初始化并迭代若干组独立的初始值，最终取最优。默认值为1
init_params，weight_init，means_init：用于设定初始化值。init_params可以使用'kmeans'和'random'之间的一种，代表产生初始值的方式。也可以使用weight_init或者means_init手动传入初始化值
max_iter：最大迭代次数

接下来我们分别将高斯混合模型中的组成个数设置为4和6，并将最终结果绘制成图像。其中，左侧图像代表的是真实数据，点的颜色对应于不同的高斯分布；而右侧则为高斯混合模型的概率等高线及其对每个点的分类。

colorlists=['tab:gray','tab:purple','tab:blue','tab:green','tab:orange','tab:red']
colormaps=['Greys','Purples','Blues','Greens','Oranges','Reds']

def plot_gaussians(model,fig,axes,x,y,classtypes):
    X_mesh,Y_mesh=np.meshgrid(np.linspace(-15,15,1000),np.linspace(-15,15,1000))
    XY_mesh=np.concatenate([X_mesh.reshape(-1,1),Y_mesh.reshape(-1,1)],axis=1)
    
    mu=model.means_
    sigma=model.covariances_
    gaussian_probas=1/(2*np.pi)/np.sqrt(np.linalg.norm(sigma))*np.exp(-1/2*np.matmul(np.matmul((XY_mesh.reshape(-1,1,2)-mu).reshape(-1,mu.shape[0],1,2),np.linalg.inv(sigma)),(XY_mesh.reshape(-1,1,2)-mu).reshape(-1,mu.shape[0],1,2).transpose(0,1,3,2)))
    gaussian_probas=gaussian_probas.squeeze()
    
    
    for i in range(gaussian_probas.shape[1]):
        contour=axes.contourf(X_mesh,Y_mesh,gaussian_probas[:,i].reshape(X_mesh.shape),norm=LogNorm(vmin=0.0001, vmax=0.1),levels=np.logspace(-4,0,10),alpha=0.6,cmap=colormaps[i])
        
    
    for j in range(classtypes):
        axes.scatter(x[y==j,0],x[y==j,1],c=colorlists[j])
    
    axes.plot(mu[:,0],mu[:,1],c='black',marker='*',markersize=15,linewidth=0)
    axes.set_xlim(-12,12)
    axes.set_ylim(-12,12)
    
def plot_points(fig,axes,x,y,classtypes):
    for j in range(classtypes):
        axes.scatter(x[y==j,0],x[y==j,1],c=colorlists[j])
    
    axes.set_xlim(-12,12)
    axes.set_ylim(-12,12)

gaussian_mixture=GaussianMixture(n_components=4,n_init=50)
y_pred=gaussian_mixture.fit_predict(x)
fig=plt.figure(figsize=(16,6))
axes=fig.subplots(1,2)
plot_points(fig,axes[0],x,y,6)
plot_gaussians(gaussian_mixture,fig,axes[1],x,y_pred,6)

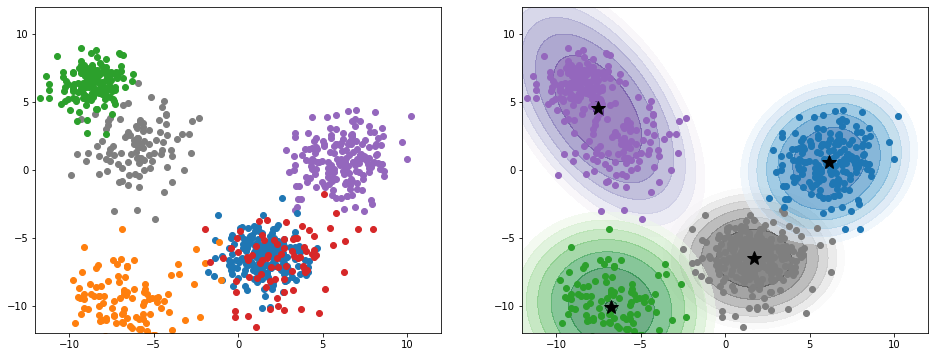
gaussian_mixture=GaussianMixture(n_components=6,n_init=50)
y_pred=gaussian_mixture.fit_predict(x)

fig=plt.figure(figsize=(16,6))
axes=fig.subplots(1,2)
plot_points(fig,axes[0],x,y,6)
plot_gaussians(gaussian_mixture,fig,axes[1],x,y_pred,6)

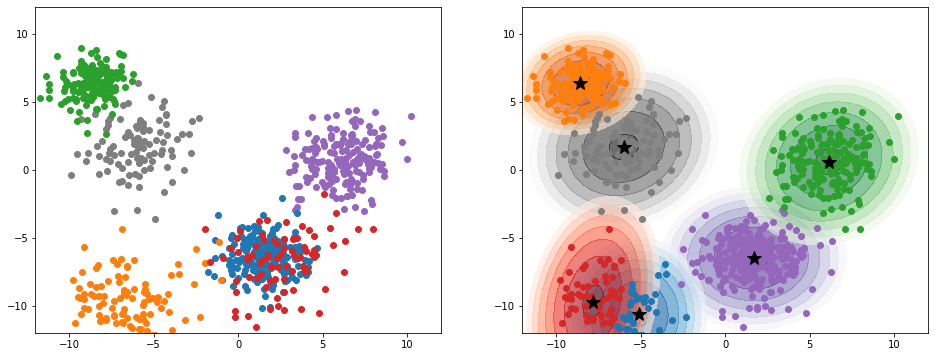
从中可以看到，高斯混合模型可以将产生于不同的高斯分布的数据点分开。但是如果两个高斯分布的中心点相聚过近，或者设置的高斯分布组成数目不合适的话，分类效果便会有所下降。

参考

统计学习方法，李航
The Elements of Statistical Learning
https://www.zhihu.com/question/40797593
https://www.zhihu.com/question/27976634
https://blog.csdn.net/v_JULY_v/article/details/81708386
Machine Learning: A Probabilistic Perspective
https://blog.csdn.net/jinping_shi/article/details/59613054/

Yufei Luo's Blog

机器学习-EM算法

概述