密码学-哈希函数

Basic concepts

Definition

A hash function (with output length \(\ell\)) is a pair of probabilistic polynomial-time algorithms \((Gen,H)\) satisfying the following:

• \(Gen\) is a probabilistic algorithm that takes as input a security parameter \(1^n\) and outputs a key \(s\). We assume that \(1^n\) is implicit in \(s\).
• \(H\) takes as input a key \(s\) and a string \(x\in \{0,1\}^*\) and outputs a string \(H^{s}(x)\in \{0,1\}^{\ell(n)}\) (\(n\) is the security parameter implicit in \(s\)).

In general case, the function takes as input strings of arbitrary length. If \(H^s\) is defined only for inputs \(x\in\{0,1\}^{\ell '(n)}\) and \(\ell '(n)>\ell(n)\), then we say that \((Gen,H)\) is a fixed-length hash function for inputs of length \(\ell '\). In this case, \(H\) is also called a compression function.

Collision resistance

First we define an collision-finding experiment \(Hash-coll_{\mathcal{A},\pi}(n)\) for a hash function \(\Pi=(Gen,H)\), an adversary \(\mathcal{A}\) and a security parameter \(n\):

1. A key \(s\) is generated by running \(Gen(1^n)\).
2. The adversary \(\mathcal{A}\) is given \(s\) and outputs \(x,x'\).
3. The output of the experiment is defined to be 1 if and only if \(x\ne x'\) and \(H^s(x)=H^s(x')\). In such a case we say that \(\mathcal{A}\) has found a collision.

A hash function \(\Pi=(Gen,H)\) is collision resistant if for all probabilistic polynomial-time adversaries \(\mathcal{A}\) there is a negligible function \(negl\) such that \[ Pr[Hash-coll_{\mathcal{A},\pi}(n)=1]\le negl(n) \]

Unkeyed hash functions

Cryptographic hash functions used in practice generally have a fixed output length and are usually unkeyed, meaning that the hash function is just a fixed function \(H:\{0,1\}^*\rightarrow \{0,1\}^\ell\). Although this is problematic theoretically since \(H\) must have a collision pair, the unkeyed cryptographic hash functions used in the real world are collision resistant for all practical purposes. It is due to the fact that colliding pairs are unknown and computationally difficult to find even though they must exist.

In proofs of security for the construction based on collision resistance of a hash function, we just assume that any efficient ways to find a collision in \(H\) can be used by the adversaries.

Weaker notions of security

In some applications, it suffices to rely on security requirements weaker than collision resistance. These include:

• Second-preimage or target-collision resistance: if given \(s\) and a uniform \(x\), it is infeasible for a PPT adversary to find \(x'\ne x\) such that \(H^s(x')=H^s(x)\). Any hash function that is collision resistant is also second preimage resistant.
• Preimage resistance: if given \(s\) and a uniform \(y\), it is infeasible for a PPT adversary to find a value \(x\) such that \(H^s(x)=y\) (this essentially means that \(H^s\) is one-way).

Domain extension: the Merkle-Damgard transform

Hash functions are often constructed by first designing a collision-resistant compression function handling fixed-length inputs, and then using domain extension to handle arbitrary-length inputs. The Merkle-Damgard transform is a common approach for extending a compression function to a full-fledged hash function, while maintaining the collision-resistance property of the former.

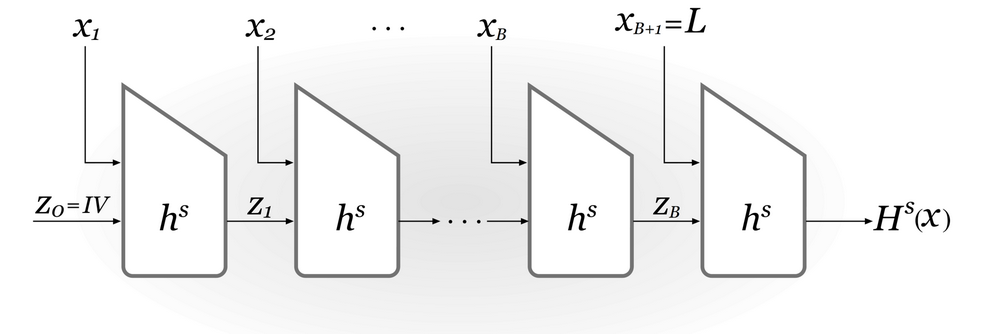
Let \((Gen,h)\) be a fixed-length hash function for inputs of length \(2n\) and with output length \(n\). Construct hash function \((Gen,H)\) as follows:

• \(Gen\): a probabilistic algorithm that takes as input a security parameter \(1^n\) and outputs a key \(s\)
• \(H\): on input a key \(s\) and a string \(x\in \{0,1\}^*\) of length \(L<2^n\), do the following:
  1. Set \(B=\lceil \frac{L}{n}\rceil\) (i.e., the number of blocks in \(x\)). Pad \(x\) with zeros so its length is a multiple of \(n\). Parse the padded result as the sequence of n-bit blocks \(x_1,\dots,x_B\). Set \(x_{B+1}=L\), where \(L\) is encoded as an n-bit string.
  2. Set \(z_0=0^n\) (this is also called the IV).
  3. For \(i=1,\dots,B+1\), compute \(z_i=h^s(z_{i-1}||x_i)\).
  4. Output \(z_{B+1}\).

The above construction is illustrated as the following figure:

Message authentication using hash functions

Hash-and-MAC

Let \(\Pi=(Mac,Vrfy)\) be a MAC for messages of length \(\ell(n)\), and let \(\Pi_H=(Gen_H,H)\) be a hash function with output length \(\ell(n)\). Construct a MAC \(\Pi'=(Gen',Mac',Vrfy')\) for arbitrary-length messages as follows:

• \(Gen'\): on input \(1^n\), choose uniform \(k\in \{0,1\}^n\) and run \(Gen_{H}(1^n)\) to obtain \(s\); the key is \(k'=<k,s>\).
• \(Mac'\): on input a key \(<k,s>\) and a message \(m\in \{0,1\}^*\), output \(t\leftarrow Mac_k(H^s(m))\).
• \(Vrfy'\): on input a key \(<k,s>\), a message \(m\in \{0,1\}^*\), and a MAC tag \(t\), output 1 if and only if \(Vrfy_k(H^s(m),t)=1\).

If \(\Pi\) is a secure MAC for messages of length \(\ell\) and \(\Pi_H\) is collision resistant, then the above construction is a secure MAC for arbitrary-length messages.

HMAC

If \(H\) is constructed using the Merkle-Damgard transform (and the most real-world hash functions are), then a MAC designed in this way is completely insecure (why?). Instead, two layers of hashing is used.

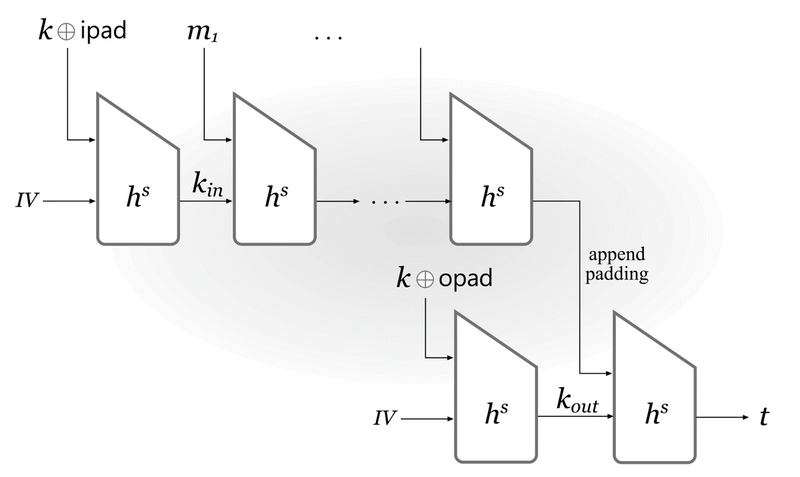
Let \((Gen_H,H)\) be a hash function constructed by applying the Merkle-Damgard transform to a compression function \((Gen_H,h)\) taking inputs of length \(n+n'\). Let \(ipad\) and \(opad\) be fixed constants of length \(n'\). Define a MAC as follows:

• \(Gen\): on input \(1^n\), run \(Gen_H(1^n)\) to obtain a key \(s\). Also choose uniform \(k\in \{0,1\}^{n'}\). Output the key \(<s,k>\).
• \(Mac\): on input a key \(<s,k>\) and a message \(m\in \{0,1\}^*\), output \(t:=H^s((k~xor~opad)||H^s((k~xor~ipad)||m))\).
• \(Vrfy\): on input a key \(<s,k>\), a message \(m\in \{0,1\}^*\), and a tag \(t\), output 1 if and only if \(t=H^s((k~xor~opad)||H^s((k~xor~ipad)||m))\).

The HMAC construction is illustrated as the following figure:

Generic attacks on hash functions

Birthday attacks

The collision-finding algorithm we have described is often called a birthday attack.The birthday problem is the following: if \(q\) people are in a room, what is the probability that two of them have the same birthday? (Assume birthdays are uniformly and independently distributed among the 365 days of a non-leap year.)

For \(y_1,\dots,y_q\) chosen uniformly in \(\{1,\dots,N\}\), the probability of a collision is roughly 1/2 when \(q=\Theta(N^{1/2})\). So, for a hash function to resist collision-finding attacks that run in time \(T\), the output length of the hash function needs to be at least \(2\log T\) bits.

Small-space birthday attacks

The small-space birthday attack has similar time complexity and success probability as birthday attacks, but require drastically reduced memory requirements (use constant memory). The attack begins by choosing a random value \(x_0\) and then computing \(x_i:=H(x_{i-1})\) and \(x_{2i}:=H(H(x_{2(i-1)}))\) for \(i=1,2,\dots\). In each step the values \(x_i\) and \(x_{2i}\) are compared; if they are equal then there is a collision somewhere in the sequence \(x_0,x_1,\dots,x_{2i-1}\).

Additional application of hash functions

• Fingerprinting & Deduplication:

  When using a collision-resistant hash function \(H\), the hash of a file \(H(x)\) can be used as a unique identifier of the file \(x\). One can check the hashes of two files to determine whether they are equal. This idea is used in many applications like virus fingerprinting, file deduplication, P2P file sharing, etc.

• Password hashing:

  The user's passward \(pw\) is stored by a hash of the password \(H(pw)\) instead of a password itself. To prevent exhaustive decryption from an attacker, one way is to use "slow" hash functions (i.e., compute \(H^{I}(pw)\) for \(I>>1\)), and another way is to introduce a salt (i.e., a long random value \(s\) unique to the user)

• Key derivation:

  A key-derivation function provides a way to obtain a uniformly distributed string from any distribution with high (computational) min-entropy.

• Commitment scheme:

  A commitment scheme allows one party to “commit” to a message \(m\) by sending a commitment value \(com\), with \(com\) reveals nothing about \(m\) and \(com\) cannot later “open” as two different messages. To commit to a message \(m\), the sender chooses uniform \(r \in \{0, 1\}^n\) and outputs \(com := H(m||r)\).

Practical applications

Hash function from block ciphers

It is possible to build a collision-resistant compression function from a block cipher. One of the most common ways is via the Davies-Meyer construction.

Let \(F\) be a block cipher with \(n\)-bit key length and \(\ell\)-bit block length. The compression function \(h:\{0,1\}^{n+\ell}\rightarrow \{0,1\}^{\ell}\) is defined as \(h(k,x)=F_{k}(x)\oplus x\).

If \(F\) is modeled as an ideal cipher, then the Davies–Meyer construction yields a collision-resistant compression function. However, when instantiating the Davies-Meyer construction with concrete block ciphers, the ciphers should be designed specially for this purpose (block ciphers designed for encryption like DES and AES should not be used).

MD5

MD5 is a hash function with a 128-bit output length. Today, the collisions in MD5 can be found within one minute. So MD5 should not be used anywhere cryptographic security is needed.

The detail of MD5 algorithm can refer to:

• https://www.zhihu.com/question/278134292
• https://blog.csdn.net/goodnameused/article/details/81068697

SHA family

The Secure Hash Algorithm (SHA) refers to a series of cryptographic hash functions standardized by NIST.

SHA-1 has a 160-bit output length. Theoretical analysis over the past few years indicates that collisions in SHA-1 can be found using significantly fewer than the \(2^{80}\) hash-function evaluations, and it is conjectured that a collision will be found soon. So it is recommended to be replaced by more secure hash algorithms. The details of SHA-1 can refer to: https://blog.csdn.net/cmqwan/article/details/82414954

SHA-2 is a group of hash functions includes SHA-224, SHA-256, SHA-384, SHA-512, etc. SHA-2 is recommended to use in applications. The principle of SHA-256 can refer to: https://blog.csdn.net/jerry81333/article/details/78566418.

SHA-3(Keccak) was chosen as the next-generation replacement of SHA-2. The structure of SHA-3 is very different from SHA-1 and SHA-2. Refer to the following pages for details: https://blog.csdn.net/chengqiuming/article/details/82819769, https://blog.csdn.net/BlackNight168/article/details/82952489

References

1. Introduction to Modern Cryptography, Second Edition.
2. Understanding Cryptography: A Textbook for Students and Practitioners (Chinese Version).