Computational secure encryption

Perfect secrecy

Perfect secrecy: absolutely no information is leaked, even the eavesdropper has unlimited computational power(not practical in reality so it could be compromised in implementation).

Two attacks apply regardless of how the encryption scheme is constructed:

Brute force attack: the adversary decrypt $c$ using all keys $k\in \mathcal{K}$.
Random attack: the adversary guess a uniform key $k\in \mathcal{K}$ and check to see whether $Dec_{k}(c_{i})=m_{i}$ for all $i$, which has success probability $\frac{1}{|\mathcal{K}|}$.

Introducting relaxations of perfect secrecy are essential for achieving practical encryption schemes!

Computational secrecy

Definitions

Computational secrecy: incorporates two relaxations relative to theoretic definitions of security

Security is only guaranteed against efficient adversaries that run for some feasible amount of time.
Adversaries can potentially succeed with very small probability.

Approaches

Two general approaches to realize computational secrecy:

The concrete approach

Definition: A scheme is $(t, \epsilon)$-secure if any adversary running for time at most $t$ succeeds in breaking the scheme with probability at most $\epsilon$.

In practice, precise concrete guarantees are diffcult to provide(The uncertainty of computing power, algorithm, etc).

The asymptotic approach

Definition: A scheme is secure if any PPT(probabilistic polynomial-time, i.e. randomized algorithm running in time polynomial in $n$, which could be defined to be efficient) adversary $\mathcal{A}$ carrying out an attack of some formally specied type, and for every positive polynomial $p$, there exists an integer $N$ such that when $n>N$ the probability that $\mathcal{A}$ succeeds in the attack is less than $\frac{1}{p(n)}$ (i.e. negligible success probability).

Please note that nothing is guaranteed for values $n\le N$!

Example: an adversary running for $n^3$ minutes can succeed in breaking the scheme with probability $2^{40-n}$. For $n=50$, the adversary running for 3 months could only succeed with probability roughly $\frac{1}{1000}$, while for $n\le 40$ the adversary can definitely succeed within 6 weeks.

Negligible function: a function $f$ from natural numbers $n$ to the non-negative real numbers is negligible if for every positive polynomial $p(n)$ there is an N such that for all integers $n>N$ it holds that $f(n)<\frac{1}{p(n)}$. E.g. $f(n)=2^{-n}$.

Closure properties for negligible functions:

$negl_{3}=negl_{1}+negl_{2}$ is negligible.
For any positive polynomial $poly$, $negl_{4}=poly\cdot negl_{1}$ is negligible.

Proof by reduction

To prove that a given encryption construction is computationally secure, we must rely on unproven assumptions (mostly $P\ne NP$) which is hard mathematically unless it's information-theoretically secure.

Steps of proof by reduction:

Assuming some efficient (i.e. probabilistic polynomial-time) adversary $\mathcal{A}$ attacking $\Pi$ with succcess probability $\epsilon(n)$.
Construct an efficient algorithm $\mathcal{A}'$, called the "reduction", that attempts to solve problem X using adversary $\mathcal{A}$ as a subroutine. $\mathcal{A}'$ knows nothing about $\mathcal{A}$ except that $\mathcal{A}$ is attacking $\Pi$. Given some input instance x of problem X, algorithm $\mathcal{A}'$ will simulate for $\mathcal{A}$ an instance of $\Pi$ that:
- The view of $\mathcal{A}$ when run as a subroutine by $\mathcal{A}'$ should be distributed identically to (or at least close to) the view of $\mathcal{A}$ when it interacts with $\Pi$ itself.
- If $\mathcal{A}$ succeeds in breaking the instance of $\Pi$ that simulated by $\mathcal{A}'$, this should allow $\mathcal{A}'$ to solve the instance x it was given, at least with inverse polynomial probability $1/p(n)$.
1 & 2 imply that $\mathcal{A}'$ solves X with probability $\epsilon(n)/p(n)$. If $\epsilon(n)$ is negligible, then neither is $\epsilon(n)/p(n)$.
Given our assumption regarding X, we conclude that no efficient adversary $\mathcal{A}$ can succeed in breaking $\Pi$ with non-negligible probability. i.e. $\Pi$ is computational secure.

Constructing secure encryption schemes

Private-key encryption scheme

Private-key encryption scheme: A tuple of probability polynomial-time algorithms $(Gen, Enc, Dec) $ that

The key-generation algorithm $Gen$ takes as input $1^{n}$ (i.e. the security parameter is fixed) and outputs a key $k$, i.e. $k\leftarrow Gen(1^{n})$(emphasizing that Gen is a randomized algorithm). Without loss of generality, assuming that $|k|\ge n$.
The encryption algorithm $Enc$ takes a key $k$ and a plaintext message $m\in \{0, 1\}^*$ as input and outputs a ciphertext $c$. Since Enc might be randomized, we write it as $c\leftarrow Enc_{k}(m)$.
The decryption algorithm $Dec$ takes a key $k$ and a ciphertext $c$ as input and outputs a message $m$ or an error. Assuming that Dec is deterministic, so we write $m=Dec_{k}(c)$.

It's required that for every $n$, every $k\leftarrow Gen(1^n)$ and every message $m\in {0, 1}^*$, it always holds that $Dec_{k}(Enc_{k}(m))=m$.

Note that the definition considers stateless schemes, in which each invocation of $Enc$ and $Dec$ is independent of all prior invocations.

Basic definition of security

Adversarial indistinguishability experiment

The adversarial indistinguishability experiment $PrivK_{\mathcal{A},\pi}^{eav}(n)$:

The adversary $\mathcal{A}$ outputs a pair of messages $m_{0}, m_{1}\in \mathcal{M}$ with $|m_{0}|=|m_{1}|$ (no limitation with the length itself).
A key $k$ is generated by running $Gen(1^n)$, and a uniform bit $b\in \{0, 1\}$ is chosen. Challenge ciphertext $c\leftarrow Enc_{k}(m_{b})$ is computed and given to $\mathcal{A}$.
$\mathcal{A}$ outputs a bit $b'$.
The output of the experiment is 1 if $b'=b$, and 0 otherwise. We say $PrivK_{\mathcal{A},\pi}^{eav}(n)=1$ if the output of the experiment is 1 and in this case we say that $\mathcal{A}$ succeeds.

The modification in the definition of adversarial indistinguishability experiment $PrivK_{\mathcal{A}, \pi}^{eav}$:

The adversaries running in polynomial time rather than unbounded running time.
The adversary might determine the encrypted message with probability negligibly better than $\frac{1}{2}$.
The experiment is parameterized with a security parameter $n$, for both running time and success probability.
The experiment requires two messages $m_{0}$, $m_{1}$ with equal length.

EAV-secure

EAV-secure: a private-key encryption scheme $\Pi=(Gen, Enc, Dec)$ has indistinguishable encryptions in the presence of an eavesdropper if all probabilistic polynomial-time adversaries $\mathcal{A}$ there is a negligible function $negl$ such that, for all $n$, \[ Pr[PrivK_{\cal{A}, \pi}^{eav}(n)]\le \frac{1}{2}+negl(n) \]

An equivalent formulation: \[ |Pr[out_{\cal{A}}(PrivK_{\cal{A}, \pi}^{eav}(n,0))=1]-Pr[out_{\cal{A}}(PrivK_{\cal{A}, \pi}^{eav}(n,1))=1]|\le negl(n) \] $PrivK_{\mathcal{A}, \pi}^{eav}(n,b)$ means that the fixed bit $b$ is used in the experiment, i.e. the encrypted message is determined rather than random.

Note: the default notion of secure encryption does not require to hide the plaintext length, and all commonly used encryption schemes reveal the plaintext length, since it is impossible to support arbitrary-length messages while hiding information about the plaintext length. But sometimes leaking the plaintext length is problematic. E.g. simple numeric/text data, database searches, auto-suggestions, etc.. By padding them to pre-determined length before encrypting could mitigate or prevent the leakage.

Pseudorandom generators & Stream cipher

Pseudorandom generator: let $\ell$ (called the expansion factor) be a polynomial and let $G$ be a deterministic polynomial-time algorithm such that for any $n$ and any input $s\in \{0, 1\}^n$, the result $G(s)$ is a string of length $\ell(n)$. We say that $G$ is a pseudorandom ("uniform looking") generator if the following conditions hold:

Expansion: for every $n$ it holds that $\ell(n)>n$
Pseudorandomness: for any PPT algorithm $D$, there is a negligible function $negl$ such that \[ |Pr[D(G(s))=1]-Pr[D(r)=1]|\le negl(n) \] where the first probability is taken over uniform choice of $s\in \{0, 1\}^n$ and the randomness of $D$, and the second probability is taken over uniform choice $r\in \{0, 1\}^{\ell(n)}$ and the randomness of $D$.

The seed for a pseudorandom generator is analogous to the cryptographic key used by an encryption scheme, so the seed must be chosen uniformly and be kept secret from any adversary. And $s$ must be long enough to make it infeasible to numerate all possible seeds.

Stream ciphers are used to instantiate pseudorandom generators. The pseudorandom output bits are produced gradually and on demand, so the application can request exactly as many pseudorandom bits as needed, which improves efficiency and flexibility.

Pseudorandom pad

Definition

Pseudorandom pad: Let $G$ be a pseudorandom generator with expansion factor $\ell$ (please note that the expansion factor is fixed in this definition, so do not confuse with the definition of stream cipher above). Define a private-key encryption scheme for messages of length $\ell$ as follows:

$Gen$: on input $1^n$, choose uniform $k\in \{0,1\}^n$ and output it as the key. ($|G(k)|$ could be much larger than $n$ so that's why we use it).
$Enc$: on input key $k\in \{0,1\}^n$ and a message $m\in \{0,1\}^{\ell(n)}$, output the ciphertext $c:=G(k)~XOR~m$.
$Dec$: on input key $k\in \{0,1\}^n$ and a ciphertext $c\in \{0,1\}^{\ell(n)}$, output the message $m:=G(k)~XOR~c$.

If $G$ is a pseudorandom generator, then the above construction is a fixed-length private-key encryption scheme that has indistinguishable encryptions in the presence of an eavesdropper.

Proof by reduction

let $\Pi$ denote the construction of pseudorandom pad. $\mathcal{A}$ satisfies the definition of EAV-secure. i.e. for any probabilistic polynomial-time adversary $\mathcal{A}$ there is a negligible function $negl$ satisfies: $Pr[PrivK_{\mathcal{A},\pi}^{eav}(n)=1]\le \frac{1}{2}+negl(n)$.

Constructing a distinguisher $D$ based on $\mathcal{A}$: $D$ is given a string $w\in \{0, 1\}^{\ell(n)}$ as input.

Run $\mathcal{A}$$(1^{n})$ to obtain a pair of messages $m_{0}, m_{1}\in \{0, 1\}^{\ell(n)}$.
Choose a uniform bit $b\in \{0, 1\}$. Set $c:=w~XOR~m_b$.
Give $c$ to $\mathcal{A}$ and obtain output $b'$. Output 1 if $b'=b$, and output 0 otherwise.

Let $\tilde{\Pi}=(\tilde{Gen},\tilde{Enc},\tilde{Dec})$ denote the exactly one-time pad encryption scheme. Perfect secrecy of one-time pad implies that $Pr[PrivK_{\mathcal{A},\tilde{\pi}}^{eav}(n)=1]=\frac{1}{2}$.

If $w$ is chosen uniformly from $\{0,1\}^{\ell(n)}$, then the view of $\mathcal{A}$ when run as a subroutine by $D$ is distributed identically to the view of $\mathcal{A}$ in experiment $PrivK_{\mathcal{A},\tilde{\pi}}^{eav}(n)$. So we have \[ Pr_{w\leftarrow \{0,1\}}^{\ell(n)}[D(w)=1]=Pr[PrivK_{\cal{A},\tilde{\pi}}^{eav}(n)]=\frac{1}{2} \]
If $w$ is generated by choosing uniform $k\in \{0,1\}^n$ and then setting $w:=G(k)$, then the view of $\mathcal{A}$ when run as a subroutine by $D$ is distributed identically to the view of $\mathcal{A}$ in experiment $PrivK_{\mathcal{A},\tilde{\pi}}^{eav}(n)$. Thus, \[ Pr_{k\leftarrow \{0,1\}}^{n}[D(G(k))=1]=Pr[PrivK_{\cal{A},\pi}^{eav}(n)] \]

Since $G$ is a pseudorandom generator, there is a negligible function $negl$ such that \[ |Pr_{w\leftarrow \{0,1\}}^{\ell(n)}[D(w)=1]-Pr_{k\leftarrow \{0,1\}}^{n}[D(G(k))=1]|\le negl(n) \] Combining the above three equations, we can get $|\frac{1}{2}-Pr[PrivK_{\mathcal{A},\pi}^{eav}(n)]|\le negl(n)$, i.e. $Pr[PrivK_{\mathcal{A},\pi}^{eav}(n)]\le \frac{1}{2}+negl(n)$.

CPA-secure encryption schemes

Security for multiple encryptions

The multiple-message eavesdropping experiment $PrivK_{\mathcal{A},\pi}^{multi}(n)$:

The adversary $\mathcal{A}$ is given input $1^n$, and outputs a pair of equal-length lists of messages $\overrightarrow{M_0}=(m_{0,1},\dots,m_{0,t})$ and $\overrightarrow{M_1}=(m_{1,1},\dots,m_{1,t})$, with $|m_{0,i}|=|m_{1,i}|$ for all $i$.
A key $k$ is generated by running $Gen(1^n)$, and a uniform big $b\in \{0,1\}$ is chosen. For all $i$, the ciphertext $c_{i}\leftarrow Enc_{k}(m_{b,i})$ is computed and the list $\overrightarrow{C}=(c_{1},\dots,c_{t})$ is given to $\mathcal{A}$.
$\mathcal{A}$ outputs a bit $b'$.
The output of the experiment is defined to be 1 if $b'=b$, and 0 otherwise.

A private-key encryption scheme $\Pi=(Gen,Enc,Dec)$ has indistinguishable multiple encryptions in the presense of an eavesdropper if for all probabilistic polynomial-time adversaries $\mathcal{A}$ there is a negligible function $negl$ such that \[ Pr[PrivK_{\cal{A},\pi}^{multi}(n)=1]\le \frac{1}{2}+negl(n) \]

There is a private-key encryption scheme that has indistinguishable encryptions in the presence of an eavesdropper, but not indistinguishable multiple encryptions in the presence of an eavesdropper. (Consider $\mathcal{A}$ attacking one-time pad encryption with $\overrightarrow{M_{0}}=(0^{\ell},0^{\ell})$ and $\overrightarrow{M_{1}}=(0^{\ell},1^{\ell})$)

Necessity of probabilistic encryption: if $\Pi$ is a stateless encryption scheme in which $Enc$ is a deterministic function of the key and the message, then $\Pi$ cannot have indistinguishable multiple encryptions in the presence of an eavesdropper. i.e. the encryption should be randomized for encrypting multiple messages.

Chosen-Plaintext Attacks and CPA security

CPA indistinguishability experiment

The CPA(Chosen-Plaintest Attacks) indistinguishability experiment $PrivK_{\mathcal{A},\pi}^{cpa}(n)$:

A key is generated by running $Gen(1^n)$.
The adversary $\mathcal{A}$ is given input $1^{n}$ and oracle access to $Enc_{K}(\cdot)$, and outputs a pair of messages $m_{0}, m_{1}$ of the same length.
A uniform bit $b\in \{0,1\}$ is chosen, and then a ciphertext $c\leftarrow Enc_{k}(m_{b})$ is computed and given to $\mathcal{A}$.
The adversary $\mathcal{A}$ continues to have oracle access to $Enc_{K}(\cdot)$, and outputs a bit $b'$.
The output of the experiment is defined to be 1 if $b'=b$, and 0 otherwise. The former case means that $\mathcal{A}$ succeeds.

A private-key encryption scheme $\Pi=(Gen, Enc, Dec)$ has indistinguishable encryptions under a chosen-plaintext attack, or is CPA-secure, is for all probabilistic polynomial-time adversaries $\mathcal{A}$ there is a negligible function $negl$ such that \[ Pr[PrivK_{\cal{A},\pi}^{cpa}(n)=1]\le \frac{1}{2}+negl(n) \]

LR-oracle experiment

The above definition of CPA-secure can be extended to the case of multiple encryptions by using lists of plaintexts.

The LR-oracle(left-or-right) experiment $PrivK_{\mathcal{A},\pi}^{LR-cpa}(n)$:

A key $k$ is generated by running $Gen(1^{n})$.
A uniform bit $b\in \{0,1\}$ is chosen.
The adversary $\mathcal{A}$ is given input $1^{n}$ and oracle access to $LR_{k,b}(m_{0,1},m_{1,1}),\dots,LR_{k,b}(m_{0,t},m_{1,t})$ (The function $LR_{k,b}(\cdot,\cdot)$ randomly choose one of the two input texts and return the encrypted text).
The adversary $\mathcal{A}$ outputs a bit $b'$.
The output of the experiment is defined to be 1 if $b'=b$ and 0 otherwise. In the former case we say that $\mathcal{A}$ succeeds.

Private-key encryption scheme $\Pi$ has indistinguishable multiple encryptions under a chosen-plaintext attack, or is CPA-secure for multiple encryptions, if for all probabilistic polynomial-time adversaries $\mathcal{A}$ there is a negligible function $negl$ such that \[ Pr[PrivK_{\cal{A},\pi}^{LR-cpa}(n)=1]\le \frac{1}{2}+negl(n) \]

Any private-key encryption scheme that is CPA-secure is also CPA-secure for multiple encryptions.(Different from eavesdropping adversaries!)

Pseudorandom functions

Definition

Define a keyed function $F(k,x):\{0,1\}^{*}\times \{0,1\}^{*}\rightarrow \{0,1\}^{*}$ to be a two-input function, where the first input is called the key and denoted $k$. When the key is fixed, it becomes a single-input function $F_{k}(x)$. If there is a polynomial-time algorithm to compute $F$, we say $F$ is efficient. And $F$ is length-preserving if $\ell_{key}=\ell_{in}=\ell_{out}=n$.

Pseudorandom functions: let $F(k,x):\{0,1\}^{*}\times \{0,1\}^{*}\rightarrow \{0,1\}^{*}$ be an efficient, length-preserving, keyed function. F is a pseudorandom function if for all probabilistic polynomial-time distinguishers $D$, there is a negligible function $negl$ such that: \[ |Pr[D^{F_{K}(\cdot)}(1^{n})=1]-Pr[D^{f(\cdot)}(1^{n})=1]|\le negl(n) \] where the first probability is taken over uniform choice of $k\in \{0,1\}^{n}$ and the randomness of $D$, and the second probability is taken over uniform choice of $f\in Func_{n}$ and the randomness of $D$.

The set $Func_{n}$ contains all the functions that mapping n-bit strings to n-bit strings. How large is $Func_{n}$?

View the function $f\in Func_{n}$ as a large look-up table.
$f$ has $2^n$ rows(all possible n-bit strings) with each row contains a n-bit string(here the string in each row could be same). So each $f$ can be viewed as a string with $n\cdot 2^n$ bits.
For a string with $n\cdot 2^n$ bits, the number of string with this length is $2^{n\cdot 2^n}$(each bit could be 0 or 1).
So we conclude that $|Func_{n}|=2^{n\cdot 2^n}$.

Pseudorandom permutations

Let $Perm_{n}$ denotes the set of all permutations(i.e. bijections) on $\{0,1\}^{n}$. For any $f\in Perm_{n}$, we can still view it as a look-up table, but with a constraint that the entries in any two distinct rows must be different. There are $2^n$ different choices for the first row; then the second row is left with $2^{n}-1$ choices, and so on. So we can get $|Perm_{n}|=(2^{n})!$

Keyed permutation: let $F$ be a keyed funciton. If $\ell_{in}=\ell_{out}$, and for all $k\in \ell_{key}(n)$ the function $F_{k}:\{0,1\}^{\ell_{in}(n)}\rightarrow \{0,1\}^{\ell_{in}(n)}$ is a permutation, we call $F$ a keyed permutation. $\ell_{in}$ is the block length of $F$. If $\ell_{key}=\ell_{in}=n$, we say $F$ is length-preserving. And a keyed permutation is efficient if there is a polynomial-time algorithm for computing $y=F_{k}(x)$ as well as a polynomial-time algorithm for computing $x=F_{k}^{-1}(y)$.

If $F$ is a pseudorandom permutation and additionally $\ell_{in}\ge n$, then $F$ is also a pseudorandom function.

Pseudorandom permutations: Let $F:\{0,1\}^{*}\times \{0,1\}^{*}\rightarrow \{0,1\}^{*}$ be an efficient, length-preserving, keyed permutation. $F$ is a strong pseudorandom permutation if for all probabilistic polynomial-time distinguishers $D$ there exists a negligible function $negl$ such that: \[ |Pr[D^{F_{K}(\cdot),F_{K}^{-1}(\cdot)}(1^{n})=1]-Pr[D^{f(\cdot),f^{-1}(\cdot)}(1^{n})=1]|\le negl(n) \] where the first probability is taken over uniform choice of $k\in \{0,1\}^{n}$ and the randomness of $D$, and the second probability is taken over uniform choice of $f\in Perm_{n}$ and the randomness of $D$.

Pseudorandom generator using pseudorandom functions

Once we get a pseudorandom function $F$, it becomes easy to construct a pseudorandom generator $G(s)\overset{def}{=}F_{s}(1)||F_{s}(2)||\cdots ||F_{s}(\ell)$ for any desired $\ell$.

We can also use pseudorandom function to construct a stream cipher $(Init, GetBits)$ where each call to $GetBits$ outputs $n$ bits as follows:

$Init$: on input $s\in \{0,1\}^n$ and $IV\in \{0,1\}^n$, set $st_{0}:=(s,IV)$.
$GetBits$: on input $st_{i}:=(s,IV)$, compute $IV'=IV+1$ and set $y:=F_{s}(IV')$ and $st_{i+1}:=(s,IV')$. Output $(y,st_{i+1})$.

CPA-secure encryption

Definition

Let $F$ be a pseudorandom function, then a CPA-secure private-key encryption scheme for messages of length $n$ can be constructed as follows:

$Gen$: on input $1^n$, choose uniform $k\in \{0,1\}^n$ and output it.
$Enc$: on input a key $k\in \{0,1\}^n$ and a message $m\in \{0,1\}^n$, choose uniform $r\in\{0,1\}^n$ and output the ciphertext $c:=<r,F_{k}(r)~XOR~m>$.
$Dec$: on input a key $k\in \{0,1\}^n$ and a ciphertext $c=<r,s>$, output the plaintext message $m:=F_{k}(r)~XOR~s$.

Proof by reduction

Step 1:

Construct a distinguisher $D$ that is given input $1^n$ and access to an oracle $\mathcal{O}$$:\{0,1\}^{n}\rightarrow \{0,1\}^{n}$. 1. Run $\mathcal{A}$$(1^n)$. Whenever $\mathcal{A}$ queries its encryption oracle on a message $m\in \{0,1\}^{n}$, 1) choose a uniform $r\in \{0,1\}^{n}$; 2) query $\mathcal{O}$$(r)$ and get response $y$; 3) return the ciphertext $<r,y~XOR~m>$ to $\mathcal{A}$. 2. When $\mathcal{A}$ outputs messages $m_{0},m_{1}\in \{0,1\}^{n}$, choose a uniform bit $b\in \{0,1\}$ and then 1) choose uniform $r\in \{0,1\}^{n}$; 2) query $\mathcal{O}$$(r)$ and obtain response $y$; 3) return the challenge ciphertext $<r,y~XOR~m_{b}>$ to $\mathcal{A}$. 3. Continue answering encryption-oracle queries of $\mathcal{A}$ as before until $\mathcal{A}$ outputs a bit $b'$. Output 1 if $b'=b$ and 0 otherwise.

If $D$'s oracle is pseudorandom function, then the view of $\mathcal{A}$ when run as a subroutine by $D$ is distributed identically to the view of $\mathcal{A}$ in experiment $PrivK_{\mathcal{A},\pi}^{cpa}(n)$, since $k$ and $r$ are chosen uniformly. So, \[ Pr_{k\leftarrow \{0,1\}^n}[D^{F_{k}(\cdot)}(1^{n})=1]=Pr[PrivK_{\cal{A},\pi}^{cpa}(n)=1] \]
If $D$'s oracle is a random function, then the view of $\mathcal{A}$ when run as a subroutine by $D$ is distributed identically to the view of $\mathcal{A}$ in experiment $PrivK_{\mathcal{A},\tilde{\pi}}^{cpa}(n)$ ($\tilde{\pi}$ represents the encryption scheme using a truly random function $f$ instead). So, \[ Pr_{f\leftarrow Func_{n}}[D^{F_{k}(\cdot)}(1^{n})=1]=Pr[PrivK_{\cal{A},\tilde{\pi}}^{cpa}(n)=1] \]
By the assumption that $F$ is a pseudorandom function, the following inequation holds: \[ |Pr[D^{F_{K}(\cdot)}(1^{n})=1]-Pr[D^{f(\cdot)}(1^{n})=1]|\le negl(n) \]

Combining the above three equations we can get: \[ |Pr[PrivK_{\cal{A},\pi}^{cpa}(n)=1]-Pr[PrivK_{\cal{A},\tilde{\pi}}^{cpa}(n)=1]|\le negl(n) \]

Step 2:

Everytime a message $m$ is encrypted in $PrivK_{\mathcal{A},\tilde{\pi}}^{cpa}(n)$ (either by the encryption oracle or computing the challenge ciphertext), a uniform $r\in \{0,1\}^n$ is chosen and the ciphertext is set equal to $<r,f(r)~XOR~m>$.

Let $r^*$ denote the random string used when generating the challenge ciphertext $<r^{*},f(r^{*})~XOR~m_{b}>$. There are two possibilities:

The value $r^*$ is never used when answering any of $\mathcal{A}$'s encryption-oracle queries: $\mathcal{A}$ learns nothing about $f(r^{*})$ from its interaction with the encryption oracle. The value $f(r^{*})$ is uniformly distrubuted and independent of the rest of the experiment. So the probability that $\mathcal{A}$ outputs $b'=b$ in this case is exactly $1/2$.
The value $r^*$ is used when answering at lease one of $\mathcal{A}$'s encryption-oracle queries: in this case, $\mathcal{A}$ may easily determine whether $m_{0}$ or $m_{1}$ was encrypted ($\mathcal{A}$ can get $f(r^{*})$ from ciphertext $<r^*, s>$ and message $m$ by $s~XOR~m$). However, $\mathcal{A}$ makes at most $q(n)$ queries(i.e. at most $q(n)$ values of $r$), and since $r^{*}$ is chosen uniformly from $\{0,1\}^n$, the probability of this event is at most $q(n)/2^{n}$.

Let $Repeat$ denote the event that $r^*$ is used by the encryption oracle when answering at least one of $\mathcal{A}$'s queries. The probability of $Repeat$ is at most $q(n)/2^{n}$, and the probability that $\mathcal{A}$ succeeds in $PrivK_{\mathcal{A},\tilde{\pi}}^{cpa}(n)$ if $Repeat$ does not occur is exactly $1/2$. Therefore: \[ \begin{align} Pr[PrivK_{\cal{A},\tilde{\pi}}^{cpa}(n)=1] &= Pr[PrivK_{\cal{A},\tilde{\pi}}^{cpa}(n)=1\wedge Repeat]+Pr[PrivK_{\cal{A},\tilde{\pi}}^{cpa}(n)=1\wedge \overline{Repeat}] \\ &\le Pr[Repeat]+Pr[PrivK_{\cal{A},\tilde{\pi}}^{cpa}(n)=1|\overline{Repeat}] \\ &\le \frac{q(n)}{2^{n}}+\frac{1}{2} \end{align} \]

Combining the equations, we can get: \[ Pr[PrivK_{\cal{A},\pi}^{cpa}(n)=1]\le \frac{1}{2}+\frac{q(n)}{2^{n}}+negl(n) \] Since $q$ is polynomial, $q(n)/2^{n}$ is negligible. The sum of two negligible functions is still negligible, so there exists a negligible function $negl'$ such that \[ Pr[PrivK_{\cal{A},\pi}^{cpa}(n)=1]\le \frac{1}{2}+negl'(n) \] thus completing the proof.

Stream cipher revisit

Recall that the pseudorandom pad encryption is not CPA-secure since the key could only be used once, and the length of the message must be fixed and known in advance.

We already have a brief introduction about stream cipher, which can be used to address the drawbacks of pseudorandom pad encryption. In practice, stream cipher are used for encryption in two ways:

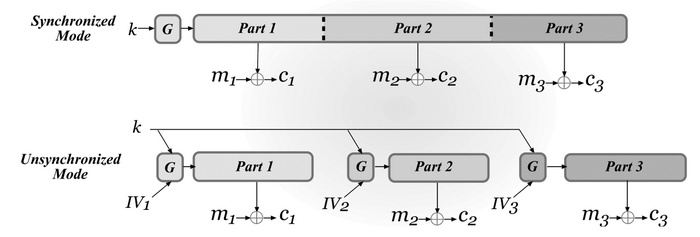
Synchronized mode: the sender and receiver must be synchronized in the sense that they know how much plaintext has been encrypted (decrypted) so far. The initialization vector $IV$ is not needed.
unsynchronized mode: the initialization vector $IV$ is needed to generate pseudorandom bits. If $IV$ is chosen uniformly, then this scheme is CPA-secure.

Block cipher

The CPA-secure scheme encryption has the drawback that the ciphertext is double the length of the plaintext. Block-cipher modes of operation provide a way of encrypting arbitrary-lengh message using shorter ciphertexts.

All the messages are seperated as several blocks $m=m_{1},m_{2},\dots m_{\ell}$ where each $m_{i}\in \{0,1\}^{n}$ represents a block of the plaintext. The block size $n$ should be sufficient large to ensure concrete security. If the message length is not a multiple of $n$, it can be padded by appending a 1 followed by sufficiently many 0s.

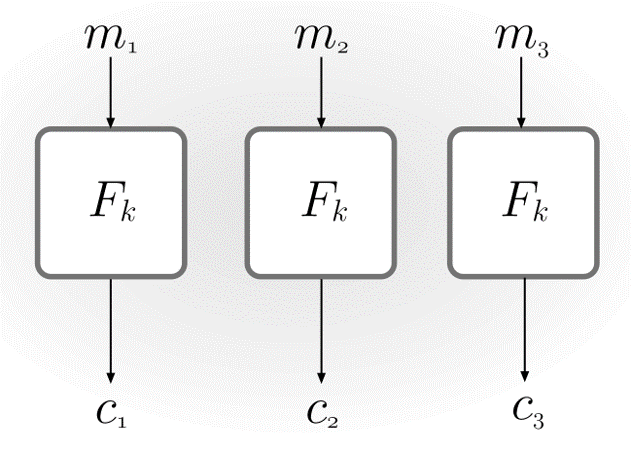
Electronic Code Book(ECB) mode

$c:=<F_{k}(m_{1}),F_{k}(m_{2},\cdots,F_{k}(m_{\ell}))>$. This mode is deterministic and therefore cannot be CPA-secure. This mode is even not indistinguishable in the presence of an eavesdropper(the block might be repeated in the plaintext which result in a repeating block in the ciphertext). This mode should not be used!

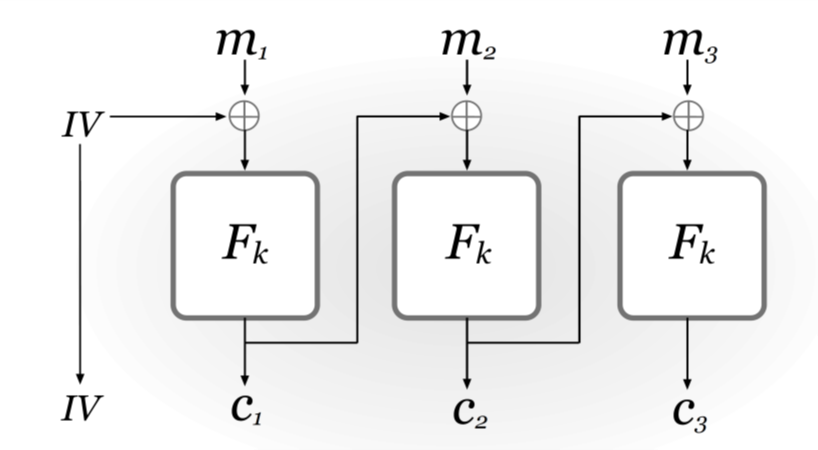
Cipher Block Chaining(CBC) mode

First choose a uniform initialization vector $IV$, then set $c_{0}:=IV$ and $c_{i}=F_{k}(c_{i-1}~XOR~m_{i})$. The final ciphertext is $<c_{0},c_{1},\dots,c_{\ell}>$. If $F$ is a pseudorandom permutation, then CBC-mode encryption is CPA-secure. But the encryption must be carried out sequentially, and $F$ should be invertible.

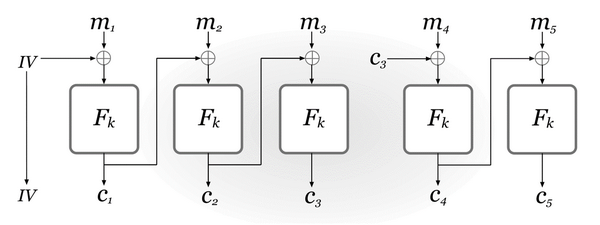
A variant of CBC-mode encryption is called chained CBC-mode, in which the last block of the previous ciphertext is used as the $IV$ when encrypting the next message. But chained CBC mode is vulnerable to a chosen-plaintext attack.

Output Feedback(OFB) mode

First choose a uniform initialization vector $IV$. Define $y_{0}:=IV$ and set $y_{i}:=F_{k}(y_{i-1})$. Each block of plaintext is encrypted by $c_{i}:=y_{i}~XOR~m_{i}$. Compared with CBC mode, OFB mode does not require $F$ be invertible, and the plaintext length is not required to be a multiple of the block length. If $F$ is a pseudorandom permutation, then OFB-mode encryption is CPA-secure.

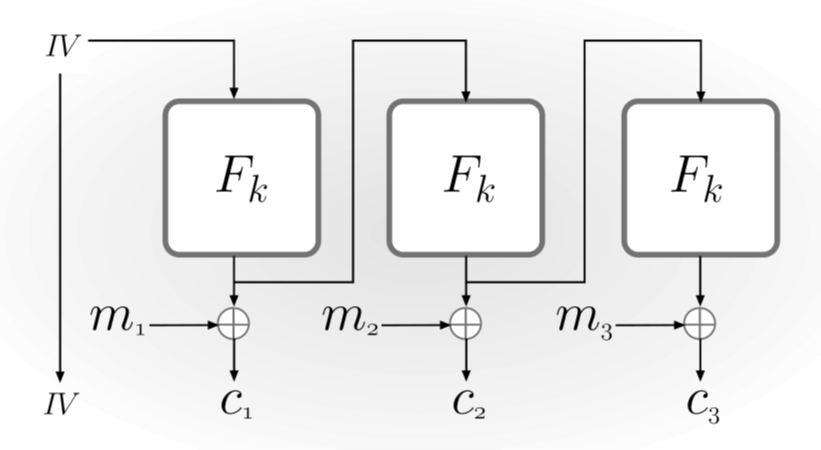
Counter(CTR) mode

First choose a uniform value $ctr\in \{0,1\}^n$. Then the pseudorandom stream is generated by computing $y_{i}:=F_{k}[(ctr+i)~mod~2^{n}]$, and the ciphertext is $c_{i}=y_{i}~XOR~m_{i}$. This encryption does not require $F$ to be invertible, or even a permutation. Also, the encryption and decryptinon can be fully parallelized. If $F$ is a pseudorandom function, then CTR-mode encryption is CPA-secure.

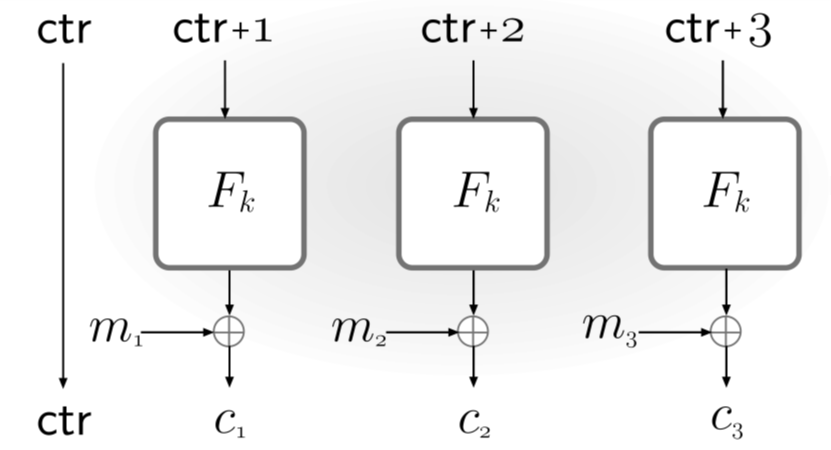
Chosen-Ciphertext Attacks

CCA-security

In a chosen-ciphertext attack, the adversary has the ability to obtain not only the encryptions of messages of its choice, but also the decryption of ciphertexts of its choice.

The CCA indistinguishability experiment $PrivK_{\mathcal{A},\pi}^{cca}(n)$:

A key $k$ is generated by running $Gen(1^n)$.
Adversary $\mathcal{A}$ is given input $1^n$ and oracle access to $Enc_{k}(\cdot)$ and $Dec_{k}(\cdot)$. It outputs a pair of messages $m_{0},m_{1}$ of the same length.
A uniform bit $b\in \{0,1\}$ is chosen, and then a ciphertext $c\leftarrow Enc_{k}(m_{b})$ is computed and given to $\mathcal{A}$. We call $c$ the challenge ciphertext.
The adversary $\mathcal{A}$ continues to have oracle access to $Enc_{k}(\cdot)$ and $Dec_{k}(\cdot)$, but is not allowed to query the latter on the challenge ciphertext itself. Eventually, $\mathcal{A}$ outputs a bit $b'$.
The output of the experiment is defined to be 1 if $b'=b$ and 0 otherwise. If the output of the experiment is 1, we say that $\mathcal{A}$ succeeds.

A private-key encryption scheme $\Pi$ has indistinguishable encryptions under a chosen-ciphertext attack, or is CCA-secure, if for all probabilistic polynomial-time adversaries $\mathcal{A}$ there is a negligible function $negl$ such that: \[ Pr[PrivK_{\cal{A},\pi}^{cca}(n)=1]\le \frac{1}{2}+negl(n) \] And any private-key encryption scheme that is CCA-secure is also CCA-secure for multiple encryptions.

Any encryption scheme that allows ciphertexts to be "manipulated" in any controlled way cannot be CCA-secure. So all the encryption scheme above is not CCA-secure!

CCA-secure encryption requires an important property called non-malleability: if the adversary tries to modify a given ciphertext, the result is either an invalid ciphertext or one that decrypts to a plaintext having no relation to the original one (message authentication).

Practical applications

Stream cipher

Linear-feedback Shift Registers

A Linear-feedback Shift Registers(LFSR) consists of an array of $n$ registers $s_{n-1},\dots,s_0$ along with a feedback loop specified by a set of $n$ feedback coefficients $c_{n-1},\dots,c_0$. The size of the array is called the degree of LFSR.

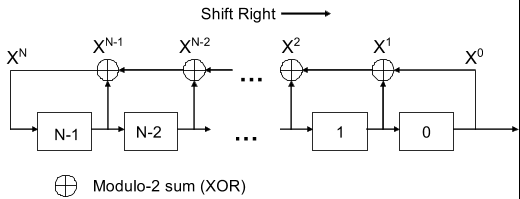
Each register stores a single bit, and the state $st$ of the LFSR at any point in time is simply the set of bits contained in the registers. The state of the LFSR is updated in each of a series of “clock ticks” by shifting the values in all the registers to the right, and setting the new value of the left-most register equal to the XOR of some subset of the current registers, with the subset determined by the feedback coefficients.

Say the state at some time $t$ is $s_{n-1}^{(t)},\dots,s_{0}^{(t)}$, then the state after the next clock tick is $s_{n-1}^{(t+1)},\dots,s_{0}^{(t+1)}$ with \[ s_{i}^{(t+1)}:=s_{i+1}^{(t)},~i=0,\dots,n-2 \] \[ s_{n-1}^{(t+1)}:=\oplus_{i=0}^{n-1}c_{i}s_{i}^{(t)} \] And the LFSR outputs the value of the right-most register $s_{0}^{(t)}$.

The state of the LFSR consists of $n$ bits, thus it can cycle through at most $2^n$ possible states. Because the all-0 state will make LFSR remains in that state forever, a maximum-length LFSR cycles through all $2^n-1$ nonzero states before repeating.

The output of a maximal-length LFSR of degree $n$ has good statistical properties. Nevertheless, it is not good pseudoramdon generators for cryptographic purposes because of the predictibility of their output. The attacker can reconstruct the entire state after observing at most $2n$ output bits using the following linear equations: \[ \begin{align} y_{n+1}=& c_{n-1}y_{n}\oplus\cdots\oplus c_{0}y_{1} \\ \cdot& \\ \cdot& \\ \cdot& \\ y_{2n}=& c_{n-1}y_{2n-1}\oplus\cdots\oplus c_{0}y_{n} \end{align} \]

To thwart reconstruction attacks, the system must introduce some nonlinearity. E.g. add nonlinearity for the left-most register or in the output sequence.

LFSRs are efficient when implemented in hardware, but have poor performance in software.

Trivium

Trivium uses three coupled, nonlinear FSRs denoted by A, B, and C and having degree 93, 84, and 111, respectively.

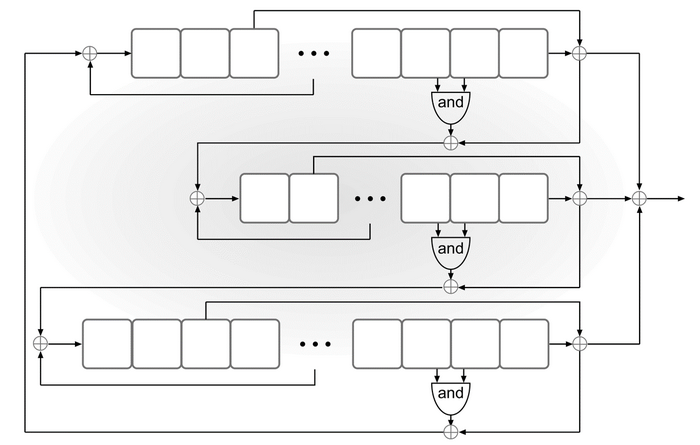
The $GetBits$ algorithm for Trivium works as follows: At each clock tick, the output of each FSR is the XOR of its right-most register and one additional register; the output of Trivium is the XOR of the output bits of the three FSRs.

The $Init$ algorithm of Trivium accepts an 80-bit key and an 80-bit IV . The key is loaded into the 80 left-most registers of A, and the IV is loaded into the 80 left-most registers of B. The remaining registers are set to 0, except for the three right-most registers of C, which are set to 1. Then $GetBits$ is run $4·288$ times (with output discarded), and the resulting state is taken as $st_0$.

To date, no cryptanalytic attacks better than exhaustive key search are known against the full Trivium cipher.

RC4

RC4 is remarkable for its speed and simplicity. Although it is widely used today, but recent attacks have shown serious cryptographic weaknesses in RC4 so it should no longer be used.

Block cipher

DES encryption scheme

Feistel networks

Feistel networks offer an approach for constructing block ciphers. An advantage of Feistel networks over substitution-permutation networks is that the underlying functions used in a Feistel network need not be invertible.

In the $i$th round of a Feistel network, the input is divided into two halves $L_{i-1}$ and $R_{i-1}$ with equal length $\ell/2$. The output $(L_{i},R_{i})$ of the round is $L_{i}:=R_{i-1}$ and $R_{i}:=L_{i-1}\oplus f_{i}(R_{i-1})$, with $f_{i}(R)=\hat{f}_{i}(k_{i},R)$ and $k_i$ is the sub-key in the $i$th round.

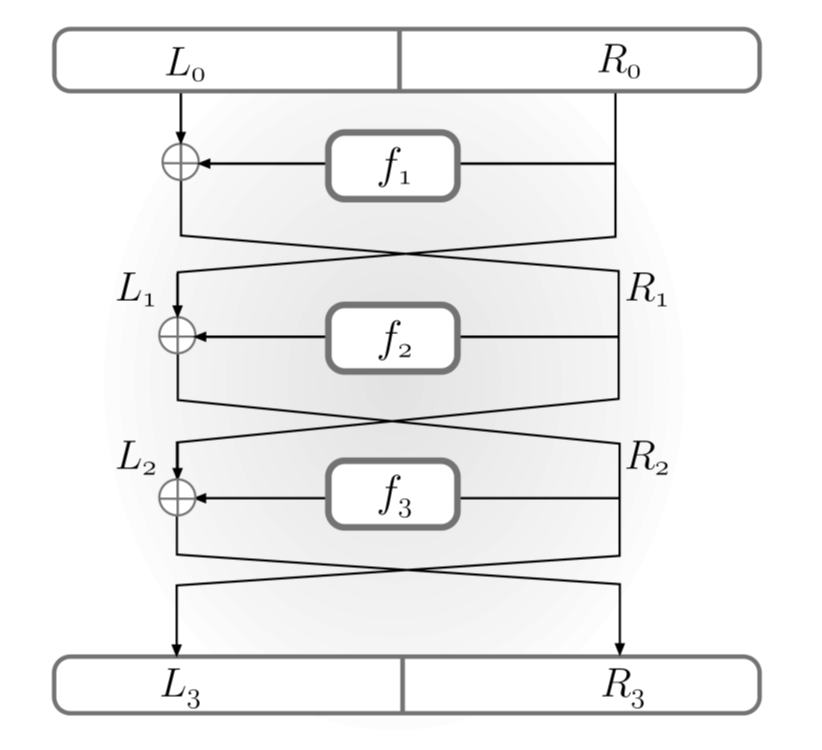
A Feistel network is invertible regardless of the $\{f_i\}$. Given the output $(L_i,R_i)$ of the $i$th round, we can compute $(L_{i-1},R_{i-1})$ as follows: first set $R_{i-1}:= L_i$, Then compute $L_{i-1}:=R_{i}\oplus f_{i}(R_{i-1})$.

DES

The DES block cipher is a 16-round Feistel network with a block length of 64 bits and a key length of 56 bits. The same round function $\hat{f}$ is used in each of the 16 rounds. The round function takes a 48-bit sub-key and a 32-bit input.

The key schedule of DES is used to derive a sequence of 48-bit sub-keys $k_{1},\dots,k_{16}$ from the 56-bit master key, with each sub-key $k_{i}$ being a permuted subset of 48 bits of the master key.

The DES round function $\hat{f}$ (or the DES mangler function) is constructed as the following figure:

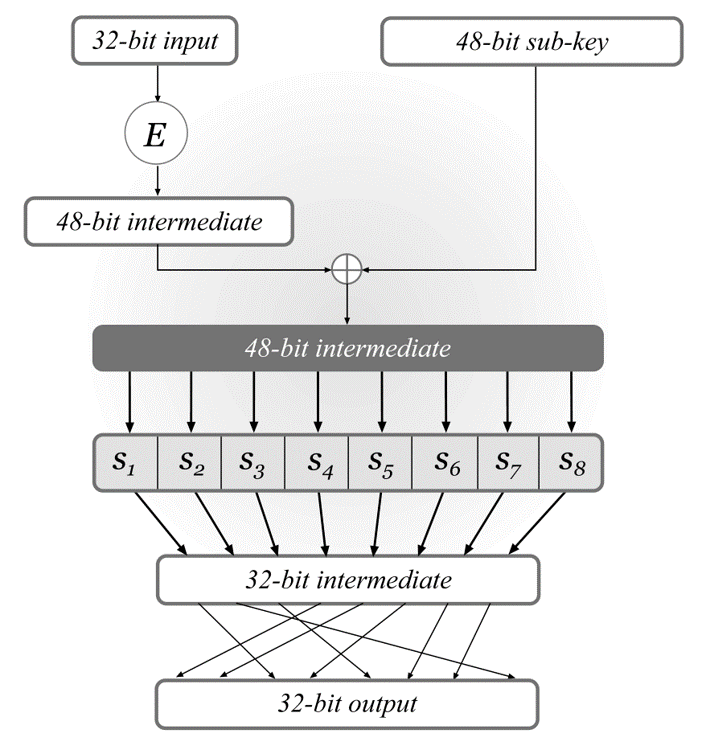
$E$ is called the expansion function, which works by simply duplicating half the bits of $R$ (according to a fixed rule). Each S-box maps a 6-bit input to a 4-bit output. Changing one bit of any input to an S-box always changes at least two bits of the output, so the DES exhibits a strong avalanche effect.

Unfortunately, the 56-bit key length of DES is short enough that an exhaustive search through all $2^{56}$ possible keys is now feasible. Using differential cryptoanalysis make the time to decrypt becomes much shorter.

3DES: Triple-DES (or 3DES) is based on a triple invocation of DES using two or three keys. There are two variants:

three keys: Choose three independent keys and define $F_{k_{1},k_{2},k_{3}}^{''}(x)=F_{k_{3}}(F_{k_2}^{-1}(F_{k_1}(x)))$.
two keys: Choose two independent keys and define $F_{k_{1},k_{2}}^{''}(x)=F_{k_{1}}(F_{k_2}^{-1}(F_{k_1}(x)))$ .

The security of the two variants is both $2^{2n}$, since the three keys encryption is susceptible to a meet-in-the-middle attack. 3DES is relatively slow and the key length is short, so it is recommended to use AES instead.

For the details of DES encryption scheme, refer to:

https://blog.csdn.net/baidu_36856113/article/details/53558795
Understanding Cryptography: A Textbook for Students and Practitioners. Chapter 3

AES encryption scheme

Substitution-permutation networks

A SPN can be viewed as a direct implementation of the confusion-diffusion paradigm. Define $S$ as a fixed public substitution function. The cipher proceeds in a series of rounds, where in each round we apply the following sequence of operations to the n-bit input $x$ of that round.

Key mixing: Set $x:=x\oplus k$, where $k$ is the current-round sub-key;
Substitution: Set $x:=S_{1}(x_{1})||\cdots||S_{n}(x_{n})$, where $x_i$ is the ith byte of $x$;
Permutation: Permute the bits of $x$ to obtain the output of the round.

The following figure is a simple example of substitution-permutation network with a 16-bit block length and 4-bit S-boxes:

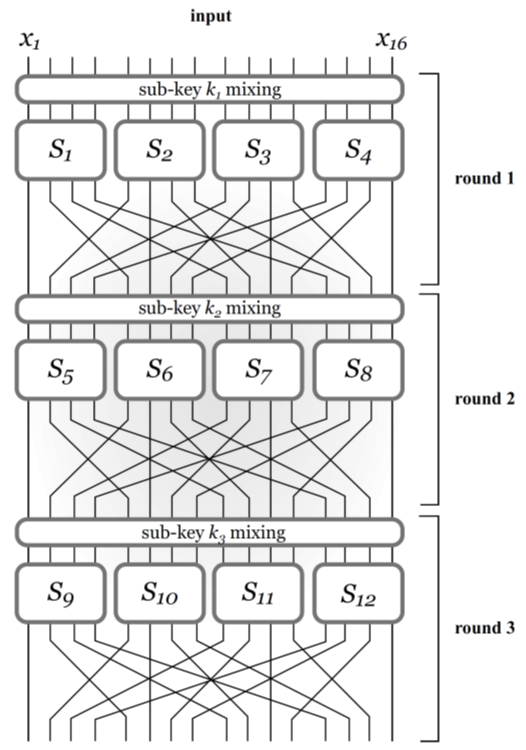
The avalanche effect: a small change in the input must “affect” every bit of the output in any block cipher. In substitution-permutation network, the avalanche effect is ensured by the following two properties:

changing a single bit of the input to an S-box changes at least two bits in the output of the S-box;
the mixing permutations makes the output bits of any given S-box are used as input to multiple S-boxes in the next round.

AES

AES is essentially a substitution-permutation network. During computation of the AES algorithm, a 4-by-4 array of bytes called the state is modified in a series of rounds. The state is initially set equal to the input to the cipher(i.e., the block size is 128 bit). The following operations are then applied to the state in a series of four stages during each round:

AddRoundKey: In every round of AES, a 128-bit sub-key is derived from the master key, and is interpreted as a 4-by-4 array of bytes. The state array is updated by XORing it with this sub-key.
SubBytes: each byte of the state array is replaced by another byte according to a single fixed lookup table S. This substitution table (or S-box) is a bijection over $\{0, 1\}^8$.
ShiftRows: the bytes in each row of the state array are shifted to the left as follows: the first row of the array is untouched, the second, third and fourth row is shifted to the left by one place, two places and three places, respectively. All shifts are cyclic.
MixColumns: an invertible transformation is applied to the four bytes in each column (i.e., a linear transformation over $GF(2^8)$).

In the final round, MixColumns is replaced with AddRoundKey.

The number of rounds depends on the key length. Ten rounds are used for a 128-bit key, 12 rounds for a 192-bit key, and 14 rounds for a 256-bit key.

AES encryption is free, standardized, efficient, and highly secure. To date, there are no practical cryptanalytic attacks that are significantly better than an exhaustive search for the key.

For the details of AES encryption scheme, refer to:

https://blog.csdn.net/qq_38289815/article/details/80900813
https://blog.csdn.net/weixin_40876133/article/details/82797732
Understanding Cryptography: A Textbook for Students and Practitioners. Chapter 4

References

Introduction to Modern Cryptography, Second Edition.
Understanding Cryptography: A Textbook for Students and Practitioners (Chinese Version).